冀教版数学九年级下册同步课件:29.2 直线与圆的位置关系(共24张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:29.2 直线与圆的位置关系(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:53:23 | ||
图片预览





文档简介
(共24张PPT)
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
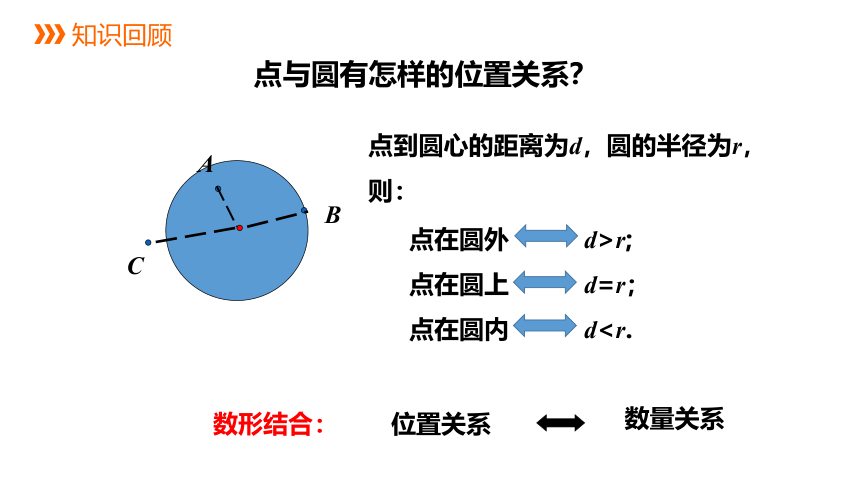
点与圆有怎样的位置关系?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 dA
B
C
位置关系
数形结合:
数量关系
知识回顾
如果我们把太阳看成一个圆,地平线看成一条直线,在日出过程中,圆和直线出现了几种不同的位置关系?
情景导入
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
地平线
●O
●O
●O
三
我们发现这个自然现象反映出直线与圆的公共点个数有 种情况
●
●
●
●
获取新知
一起探究
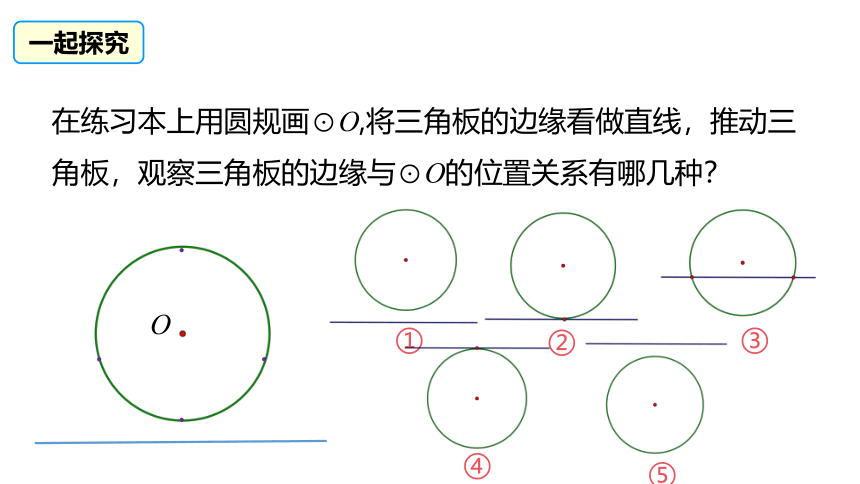
在练习本上用圆规画⊙O,将三角板的边缘看做直线,推动三角板,观察三角板的边缘与⊙O的位置关系有哪几种?
O
●
●
●
●
①
②
③
④
⑤
一起探究
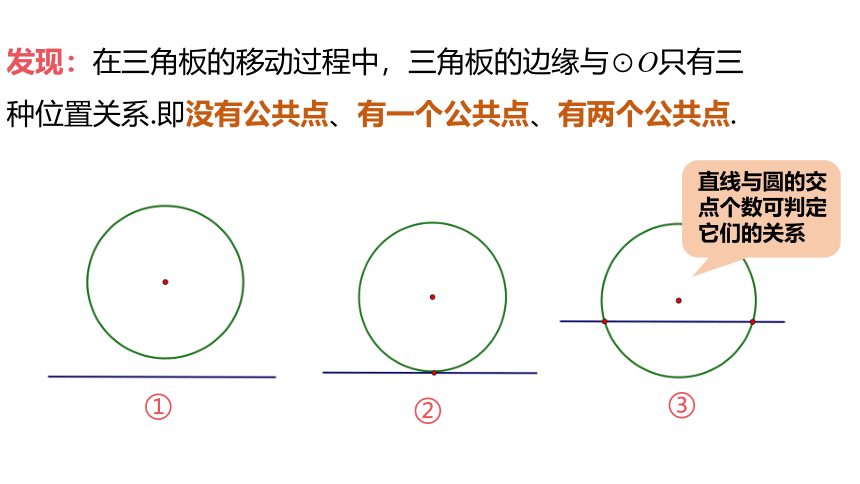
发现:在三角板的移动过程中,三角板的边缘与⊙O只有三种位置关系.即没有公共点、有一个公共点、有两个公共点.
①
②
③
直线与圆的交点个数可判定它们的关系
当直线与圆有两个公共点时,称直线与圆相交.
当直线与圆有唯一一个公共点时,称直线与圆相切,此时这个公共点叫切点,这条直线叫做圆的切线.
当直线与圆没有公共点时,称直线与圆相离.
获取新知
概 念
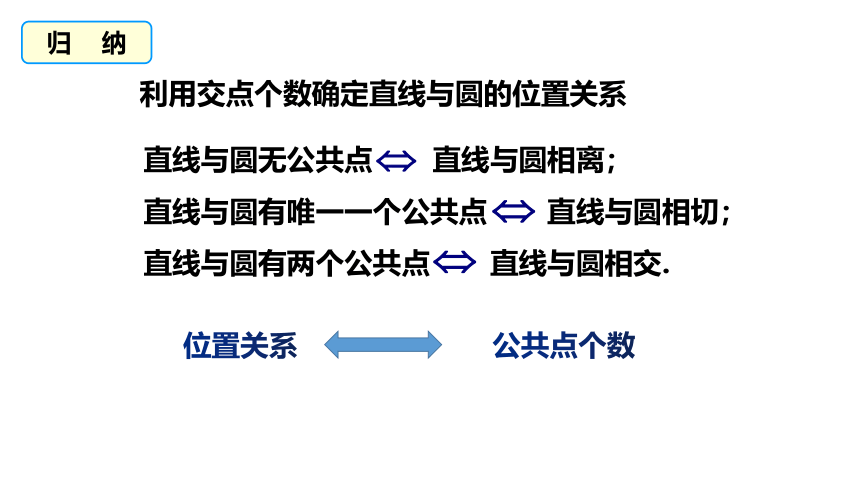
归 纳
直线与圆无公共点 直线与圆相离;
直线与圆有唯一一个公共点 直线与圆相切;
直线与圆有两个公共点 直线与圆相交.
位置关系
公共点个数
利用交点个数确定直线与圆的位置关系
O
d
设圆心到直线的距离为d,圆的半径为r,观察在直线与圆的不同位置关系中d与r的关系,你有什么发现?
d
r
d
r
d
r
d>r
d=r
d<r
一起探究
问题 与判断点与圆的位置关系类似,我们能不能也通过数量关系来判断直线与圆的位置关系?
问题 当d<r,d=r或d>r时,l与⊙O分别具有怎样的位置关系?
r
r
r
d
┐
d
┐
┐
d
O
l
P
Q
O
l
P
O
l
(1)d<r
直线和圆______
(2)d=r
直线和圆______
(3)d>r
直线和圆______
相交
相切
相离
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
位置关系
数量关系
利用数量关系确定直线与圆的位置关系
o
o
o
归 纳
B
C
A
4
3
例1 Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1) r=2cm;(2) r=2.4cm; (3) r=3cm.
分析:已知r,只需确定d的值,即求出C到AB的距离.
D
例题讲解
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
5.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm.
所以 (1)当r=2cm时,
d >r,
因此⊙C和AB相离.
B
C
A
4
3
D
d
记住:斜边上的高等于两直角边的乘积除以斜边.
(2)当r=2.4cm时,d=r.
因此⊙C和AB相切.
B
C
A
4
3
D
d
(3)当r=3cm时,有d因此,⊙C和AB相交.
B
C
A
4
3
D
d
归纳:判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 的个数来判断;
(2)由 的大小关系来判断;
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
例2 如图,已知∠MON=30°,在ON上有一点P,OP=5cm,若以点P为圆心,以R为半径作圆,试求圆的半径R的取值范围,使:
(1)射线OM与⊙O只有一个公共点;
O
P
M
N
A
分析:情况一
如图,⊙P与直线OM相切,
R=d=PA=2.5.
情况二
如图,点O在⊙P内,⊙P与射线OM有一个交点,此时R>5.
例2 如图,已知∠MON=30°,在ON上有一点P,OP=5cm,若以点P为圆心,以R为半径作圆,试求圆的半径R的取值范围,使:
(2)射线OM与⊙O有两个公共点.
O
P
M
N
分析:要使直线OM与⊙O有两个交点,需d<R,即R>2.5.
要使射线OM与⊙O有两个公共点,
则需点O在圆上或圆外.因此R≤5.
综上,2.5<R≤5时,射线OM与⊙P有两个公共点.
随堂演练
1.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有( )
A. r < 5
B. r > 5
C. r = 5
D. r ≥ 5
B
2. ⊙O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与⊙O的位置关系是( )
A. 相交或相切
B. 相交或相离
C. 相切或相离
D. 上三种情况都有可能
A
3.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与 ⊙A的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情况均有可能
C
4.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
B
5.如图,已知∠AOB=30°,M为OA边上一点,以点M为圆心,2 cm为半径作⊙M.若点M在OA边上运动,则OM=_______cm时,⊙M与OB相切.
6.在直角坐标系中,⊙M的圆心坐标是(m,0),半径是2,如果⊙M与y轴所在的直线相切,那么m=_____;如果⊙M与y轴所在的直线相交,那么m的取值范围是____________.
4
±2
-2<m<2
7.已知☉O的半径r=7cm,直线l1 // l2,且l1与☉O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
o
l1
l2
A
B
C
l2
解:(1) l2与l1在圆的同一侧:
m=9-7=2 cm
(2)l2与l1在圆的两侧:
m=9+7=16 cm
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离
1个:相切
2个:相交
d>r:相离
d=r:相切
d课堂小结
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
点与圆有怎样的位置关系?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
B
C
位置关系
数形结合:
数量关系
知识回顾
如果我们把太阳看成一个圆,地平线看成一条直线,在日出过程中,圆和直线出现了几种不同的位置关系?
情景导入
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
地平线
●O
●O
●O
三
我们发现这个自然现象反映出直线与圆的公共点个数有 种情况
●
●
●
●
获取新知
一起探究
在练习本上用圆规画⊙O,将三角板的边缘看做直线,推动三角板,观察三角板的边缘与⊙O的位置关系有哪几种?
O
●
●
●
●
①
②
③
④
⑤
一起探究
发现:在三角板的移动过程中,三角板的边缘与⊙O只有三种位置关系.即没有公共点、有一个公共点、有两个公共点.
①
②
③
直线与圆的交点个数可判定它们的关系
当直线与圆有两个公共点时,称直线与圆相交.
当直线与圆有唯一一个公共点时,称直线与圆相切,此时这个公共点叫切点,这条直线叫做圆的切线.
当直线与圆没有公共点时,称直线与圆相离.
获取新知
概 念
归 纳
直线与圆无公共点 直线与圆相离;
直线与圆有唯一一个公共点 直线与圆相切;
直线与圆有两个公共点 直线与圆相交.
位置关系
公共点个数
利用交点个数确定直线与圆的位置关系
O
d
设圆心到直线的距离为d,圆的半径为r,观察在直线与圆的不同位置关系中d与r的关系,你有什么发现?
d
r
d
r
d
r
d>r
d=r
d<r
一起探究
问题 与判断点与圆的位置关系类似,我们能不能也通过数量关系来判断直线与圆的位置关系?
问题 当d<r,d=r或d>r时,l与⊙O分别具有怎样的位置关系?
r
r
r
d
┐
d
┐
┐
d
O
l
P
Q
O
l
P
O
l
(1)d<r
直线和圆______
(2)d=r
直线和圆______
(3)d>r
直线和圆______
相交
相切
相离
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
位置关系
数量关系
利用数量关系确定直线与圆的位置关系
o
o
o
归 纳
B
C
A
4
3
例1 Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1) r=2cm;(2) r=2.4cm; (3) r=3cm.
分析:已知r,只需确定d的值,即求出C到AB的距离.
D
例题讲解
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
5.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm.
所以 (1)当r=2cm时,
d >r,
因此⊙C和AB相离.
B
C
A
4
3
D
d
记住:斜边上的高等于两直角边的乘积除以斜边.
(2)当r=2.4cm时,d=r.
因此⊙C和AB相切.
B
C
A
4
3
D
d
(3)当r=3cm时,有d
B
C
A
4
3
D
d
归纳:判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 的个数来判断;
(2)由 的大小关系来判断;
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
例2 如图,已知∠MON=30°,在ON上有一点P,OP=5cm,若以点P为圆心,以R为半径作圆,试求圆的半径R的取值范围,使:
(1)射线OM与⊙O只有一个公共点;
O
P
M
N
A
分析:情况一
如图,⊙P与直线OM相切,
R=d=PA=2.5.
情况二
如图,点O在⊙P内,⊙P与射线OM有一个交点,此时R>5.
例2 如图,已知∠MON=30°,在ON上有一点P,OP=5cm,若以点P为圆心,以R为半径作圆,试求圆的半径R的取值范围,使:
(2)射线OM与⊙O有两个公共点.
O
P
M
N
分析:要使直线OM与⊙O有两个交点,需d<R,即R>2.5.
要使射线OM与⊙O有两个公共点,
则需点O在圆上或圆外.因此R≤5.
综上,2.5<R≤5时,射线OM与⊙P有两个公共点.
随堂演练
1.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有( )
A. r < 5
B. r > 5
C. r = 5
D. r ≥ 5
B
2. ⊙O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与⊙O的位置关系是( )
A. 相交或相切
B. 相交或相离
C. 相切或相离
D. 上三种情况都有可能
A
3.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与 ⊙A的位置关系是( )
A.相离
B.相交
C.相切
D.以上三种情况均有可能
C
4.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
B
5.如图,已知∠AOB=30°,M为OA边上一点,以点M为圆心,2 cm为半径作⊙M.若点M在OA边上运动,则OM=_______cm时,⊙M与OB相切.
6.在直角坐标系中,⊙M的圆心坐标是(m,0),半径是2,如果⊙M与y轴所在的直线相切,那么m=_____;如果⊙M与y轴所在的直线相交,那么m的取值范围是____________.
4
±2
-2<m<2
7.已知☉O的半径r=7cm,直线l1 // l2,且l1与☉O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
o
l1
l2
A
B
C
l2
解:(1) l2与l1在圆的同一侧:
m=9-7=2 cm
(2)l2与l1在圆的两侧:
m=9+7=16 cm
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
1个:相切
2个:相交
d>r:相离
d=r:相切
d
