冀教版数学九年级下册同步课件:29.1 点与圆的位置关系(共19张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:29.1 点与圆的位置关系(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 497.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第二十九章 直线与圆的位置关系
29.1 点与圆的位置关系
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.如图所示的是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗
情景导入
点与圆的位置关系及其判定
足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?
获取新知
一起探究
点与圆的位置关系
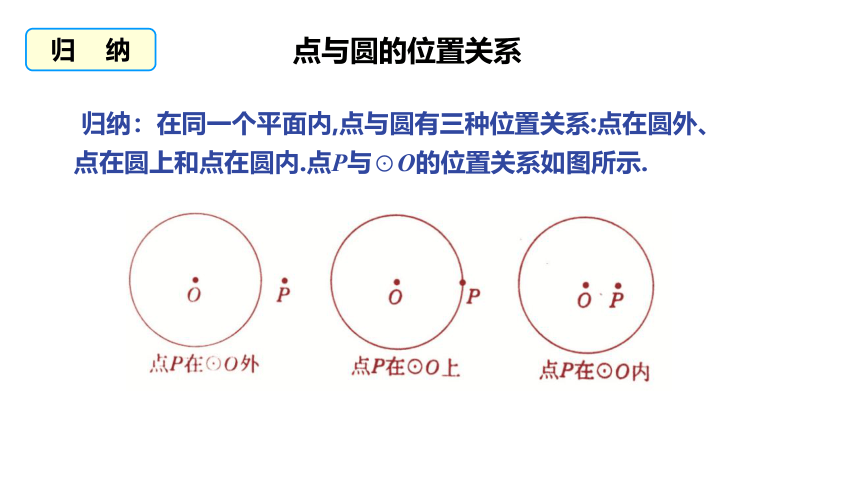
归纳:在同一个平面内,点与圆有三种位置关系:点在圆外、点在圆上和点在圆内.点P与⊙O的位置关系如图所示.
归 纳
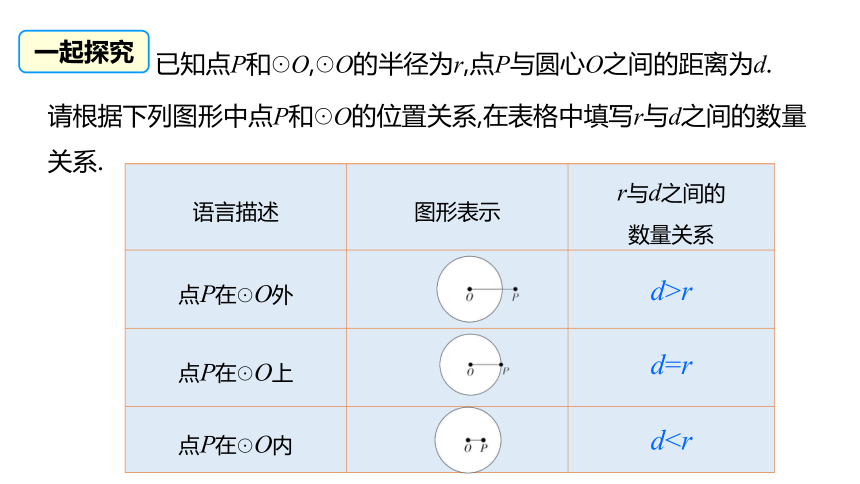
已知点P和☉O,☉O的半径为r,点P与圆心O之间的距离为d.
请根据下列图形中点P和☉O的位置关系,在表格中填写r与d之间的数量关系.
语言描述 图形表示 r与d之间的
数量关系
点P在☉O外
点P在☉O上
点P在☉O内
d>r
dd=r
一起探究
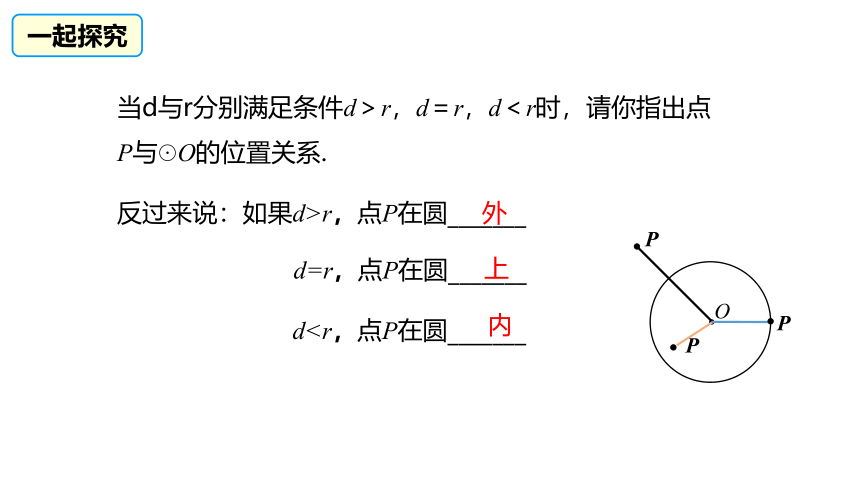
当d与r分别满足条件d>r,d=r,d<r时,请你指出点P与☉O的位置关系.
反过来说:如果d>r,点P在圆_______
d=r,点P在圆_______
d内
上
外
O
P
P
P
一起探究
点与圆的位置关系及其判定
d>r
d=r
d符号“ ”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端.
归 纳
归纳:设☉O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在☉O内 _________
(2)点P在☉O上 _________
(3)点P在☉O外 ___ ___
例1 如图,在△ABC中,∠C = 90°,AB=5 cm,BC=4 cm,以点A为圆心、3 cm为半径画圆,并判断:
(1)点C与☉A的位置关系.
(2)点B与☉A的位置关系.
(3)AB的中点D与☉A的位置关系.
A
B
C
D
例题讲解
(3)直角三角形斜边上的中线有什么性质
分析:
(1)如何判定点与圆的位置关系
(先确定点与圆心的距离,再与半径的大小进行比较可得.)
(2)在直角三角形中已知两条直角边,如何求第三边的长
(利用勾股定理求直角三角形的边长.)
(直角三角形斜边上的中线等于斜边的一半.)
(4)点C,B,D与圆心A的距离分别是多少 与半径之间的大小关系如何
(AC=3 cm=r,BC=4 cm>r,CD= AB= cm(5)根据点到圆心的距离与半径的大小之间的关系,你能分别判断点C,B,D 与☉A的位置关系吗
(点C在☉A上;点B在☉A外;点D在☉A内.)
A
B
C
D
解:已知☉A的半径r=3 cm.
(1)因为AC= =3(cm)= r,
所以点C在☉A上.
(2)因为AB=5 cm>3 cm=r,所以点B在☉A外.
(3)因为DA= AB=2.5 cm<3 cm=r,所以点D在☉A内.
A
B
C
D
例2 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,CE⊥AB于点E,以点C为圆心、3cm为半径画圆,判断点E与⊙C的位置关系.
●
B
A
E
C
∴d=CE=2.4cm,r=3cm
∴d<r
∴点E在⊙C内.
求CE的长度,还可以用什么方法?
相似
三角函数
关键:确定d与r
1.☉O的半径为4 cm,点A到圆心O的距离为3 cm,则点A与☉O的位置关系是 ( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.不能确定
A
随堂演练
2.在△ABC中,∠C=90°,AC=BC=4,点D是AB边的中点,以点C为圆心,4 cm长为半径作圆,则点A,B,C,D四点中在圆内的有( )
A.1个 B.2个 C.3个 D.4个
B
3.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
4.已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;
点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 .
OA>3
3
05.在直角三角形ABC中,∠C=90°,AC=3,AB=5.若以点C为圆心,画一个半径为3的圆,则点A,点B和⊙C的相互位置关系为( )
A.点A,点B均在⊙C内
B.点A,点B均在⊙C外
C.点A,点B均在⊙C上
D.点A在⊙C上,点B在⊙C外
D
6.如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3AC=5>r,故C点在⊙A外
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3点与圆的位置关系
设☉O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在☉O内 d(2)点P在☉O上 d=r
(3)点P在☉O外 d>r
课堂小结
第二十九章 直线与圆的位置关系
29.1 点与圆的位置关系
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.如图所示的是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗
情景导入
点与圆的位置关系及其判定
足球运动员踢出的足球在球场上滚动,在足球穿越中圈区(中间圆形区域)的过程中,可将足球看成一个点,这个点与圆具有怎样的位置关系?
获取新知
一起探究
点与圆的位置关系
归纳:在同一个平面内,点与圆有三种位置关系:点在圆外、点在圆上和点在圆内.点P与⊙O的位置关系如图所示.
归 纳
已知点P和☉O,☉O的半径为r,点P与圆心O之间的距离为d.
请根据下列图形中点P和☉O的位置关系,在表格中填写r与d之间的数量关系.
语言描述 图形表示 r与d之间的
数量关系
点P在☉O外
点P在☉O上
点P在☉O内
d>r
d
一起探究
当d与r分别满足条件d>r,d=r,d<r时,请你指出点P与☉O的位置关系.
反过来说:如果d>r,点P在圆_______
d=r,点P在圆_______
d
上
外
O
P
P
P
一起探究
点与圆的位置关系及其判定
d>r
d=r
d
归 纳
归纳:设☉O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在☉O内 _________
(2)点P在☉O上 _________
(3)点P在☉O外 ___ ___
例1 如图,在△ABC中,∠C = 90°,AB=5 cm,BC=4 cm,以点A为圆心、3 cm为半径画圆,并判断:
(1)点C与☉A的位置关系.
(2)点B与☉A的位置关系.
(3)AB的中点D与☉A的位置关系.
A
B
C
D
例题讲解
(3)直角三角形斜边上的中线有什么性质
分析:
(1)如何判定点与圆的位置关系
(先确定点与圆心的距离,再与半径的大小进行比较可得.)
(2)在直角三角形中已知两条直角边,如何求第三边的长
(利用勾股定理求直角三角形的边长.)
(直角三角形斜边上的中线等于斜边的一半.)
(4)点C,B,D与圆心A的距离分别是多少 与半径之间的大小关系如何
(AC=3 cm=r,BC=4 cm>r,CD= AB= cm
(点C在☉A上;点B在☉A外;点D在☉A内.)
A
B
C
D
解:已知☉A的半径r=3 cm.
(1)因为AC= =3(cm)= r,
所以点C在☉A上.
(2)因为AB=5 cm>3 cm=r,所以点B在☉A外.
(3)因为DA= AB=2.5 cm<3 cm=r,所以点D在☉A内.
A
B
C
D
例2 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,CE⊥AB于点E,以点C为圆心、3cm为半径画圆,判断点E与⊙C的位置关系.
●
B
A
E
C
∴d=CE=2.4cm,r=3cm
∴d<r
∴点E在⊙C内.
求CE的长度,还可以用什么方法?
相似
三角函数
关键:确定d与r
1.☉O的半径为4 cm,点A到圆心O的距离为3 cm,则点A与☉O的位置关系是 ( )
A.点A在圆内
B.点A在圆上
C.点A在圆外
D.不能确定
A
随堂演练
2.在△ABC中,∠C=90°,AC=BC=4,点D是AB边的中点,以点C为圆心,4 cm长为半径作圆,则点A,B,C,D四点中在圆内的有( )
A.1个 B.2个 C.3个 D.4个
B
3.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
4.已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;
点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 .
OA>3
3
0
A.点A,点B均在⊙C内
B.点A,点B均在⊙C外
C.点A,点B均在⊙C上
D.点A在⊙C上,点B在⊙C外
D
6.如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
设☉O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在☉O内 d
(3)点P在☉O外 d>r
课堂小结
