冀教版数学九年级上册同步课件:24.1 一元二次方程(共16张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:24.1 一元二次方程(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 198.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 12:12:18 | ||
图片预览





文档简介
(共16张PPT)
第二十四章 一元二次方程
24.1 一元二次方程
知识回顾
1.什么叫方程?我们学过哪些方程?
含有未知数的等式叫做方程.
我们学过的方程有一元一次方程,二元一次方程(组)及分式方程,其中前两种方程是整式方程.
2.什么叫一元一次方程?
含有一个未知数,且未知数的次数是1的整式方程叫做一元一次方程.
类比一元一次方程的定义,想一想:什么样的方程叫一元二次方程呢?
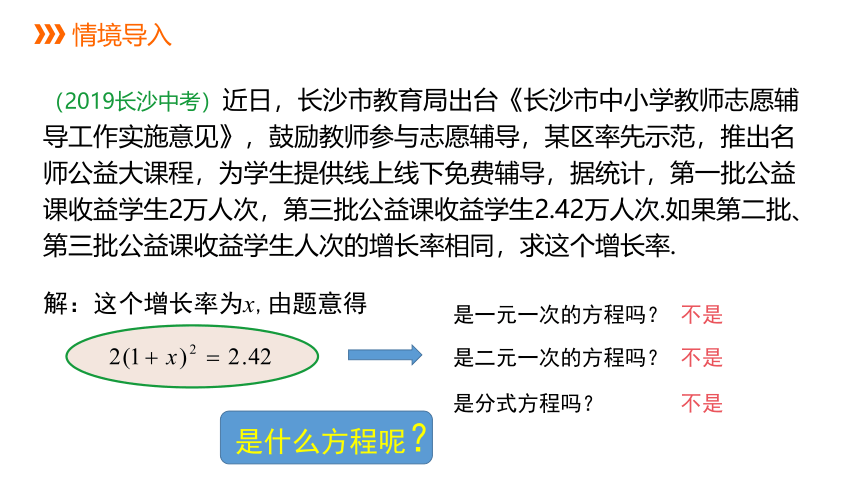
(2019长沙中考)近日,长沙市教育局出台《长沙市中小学教师志愿辅导工作实施意见》,鼓励教师参与志愿辅导,某区率先示范,推出名师公益大课程,为学生提供线上线下免费辅导,据统计,第一批公益课收益学生2万人次,第三批公益课收益学生2.42万人次.如果第二批、第三批公益课收益学生人次的增长率相同,求这个增长率.
解:这个增长率为x,由题意得
是一元一次的方程吗?
是二元一次的方程吗?
是分式方程吗?
不是
不是
不是
是什么方程呢?
情境导入
1.与一元一次方程 70x+80(60-x)=4600相比,有什么不同?
2.与二元一次方程 3x+2y=120相比,有什么不同?
5x+4y=210
未知数最高次数为2
{
只有一个未知数
3.与分式方程 相比,有什么不同?
未知数没有在分母位置,是整式方程
一元二次方程
叫什么方程合适呢?
获取新知
一起探究
我们来研究一下方程2(1+x)2=2.42的特点
注意关键点
1.一元
2.二次
3.整式
定义:只含有一个未知数,并且未知数的最高次数为2的整式方程,叫做一元二次方程.
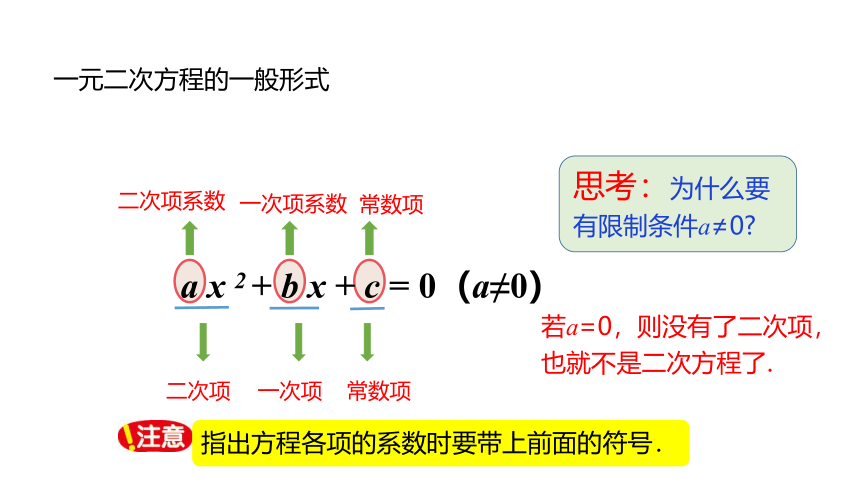
一元二次方程的一般形式
a x 2 + b x + c = 0(a≠0)
二次项系数
一次项系数
常数项
二次项
一次项
常数项
思考:为什么要有限制条件a≠0
若a=0,则没有了二次项,也就不是二次方程了.
指出方程各项的系数时要带上前面的符号.
例1 将方程3x(x-1)=5(x+2)化为一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
解: 去括号,得
其中二次项系数为3,一次项系数为-8,常数项为-10.
3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
例题讲解
获取新知
问题:类比一元一次方程,试着归纳一元二次方程根的定义.
一元一次方程的根:
使一元一次方程 的未知数的值叫做一元一次方程的解,也叫一元一次方程的根.
左右两边相等
定义: 使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解,也叫一元二次方程的根.
例题讲解
例2 判断0和-1是不是一元二次方程2x2=1-x的根.
当x=0时,左边=0,右边=1
左边≠右边
∴0不是原方程的根.
解:
当x=-1时,左边=2,右边=2
左边=右边
∴-1是原方程的根.
判断一个数值是不是一元二次方程的根的方法:
将这个值代入一元二次方程,看方程的左右两边是否相等,若相等,则是方程的根;若不相等,就不是方程的根.
例3 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛.如图要使花坛的总面积为570m2,问小路的宽应为多少?
32
20
x
思考:
1.若设小路的宽是xm,那么横向小路的面积是_____m2,纵向小路的面积是 m2,两者重叠的面积是 m2.
32x
2×20x
2x2
2.由于花坛的总面积是570m2.你能根据题意,列出方程吗?
32×20-(32x+2×20x)+2x2=570
整理以上方程可得:
x2-36x+35=0
1. 下列哪些是一元二次方程?
(1)3x+2=5x-2
(2)x2=0
(3)(x+3)(2x-4)=x2
(4)3y2=(3y+1)(y-2)
(5)x2=x3+x2-1
(6)3x2=5x-1
随堂演练
2.填空:
方程 一般形式 二次项系数 一次项系数 常数项
-2
1
3
1
3
-5
4
0
-5
3
-2
3.如图,有一张矩形纸片,长10 cm,宽 6 cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面面积是 32 cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是 x cm,根据题意可列方程为( )
A.10×6-4×6x=32
B.(10-2x)(6-2x)=32
C.(10-x)(6-x)=32
D.10×6-4x2=32
B
4.根据下列问题列方程,并将所列方程化成一元二次方程的一般形式:
(1)一个圆的面积是 6.28 cm2,求半径;
(2)一个直角三角形的两条直角边相差 3 cm,面积是 9 cm2,求较长的直角边.
解:(1)设圆的半径为rcm,则圆的面积为(πr2)cm2,
所以其一般形式为πr2-6.28=0.
(2)设较长的直角边长为acm,则较短的直角边长为(a-3)cm,
则直角三角形的面积为 cm2
所以其一般形式为a2-3a-18=0.
5.如果 2 是方程 x2-c=0 的一个根,那么常数 c 是多少?求出这个方程的其他根.
解:因为 2 是方程 x2-c=0 的一个根,
所以 22-c=0,
解得 c=4,
则原方程为 x2-4=0,即x2=4,
因为 4 的平方根为±2,
所以方程 x2-4=0 的另一个根为-2.
课堂小结
是整式方程
一元二次方程
只含有一个未知数
未知数的最高次数是2
ax2+bx+c=0(a≠0)
一元二次方程的概念
一元二次方程的一般形式
一元二次方程的解(根)
第二十四章 一元二次方程
24.1 一元二次方程
知识回顾
1.什么叫方程?我们学过哪些方程?
含有未知数的等式叫做方程.
我们学过的方程有一元一次方程,二元一次方程(组)及分式方程,其中前两种方程是整式方程.
2.什么叫一元一次方程?
含有一个未知数,且未知数的次数是1的整式方程叫做一元一次方程.
类比一元一次方程的定义,想一想:什么样的方程叫一元二次方程呢?
(2019长沙中考)近日,长沙市教育局出台《长沙市中小学教师志愿辅导工作实施意见》,鼓励教师参与志愿辅导,某区率先示范,推出名师公益大课程,为学生提供线上线下免费辅导,据统计,第一批公益课收益学生2万人次,第三批公益课收益学生2.42万人次.如果第二批、第三批公益课收益学生人次的增长率相同,求这个增长率.
解:这个增长率为x,由题意得
是一元一次的方程吗?
是二元一次的方程吗?
是分式方程吗?
不是
不是
不是
是什么方程呢?
情境导入
1.与一元一次方程 70x+80(60-x)=4600相比,有什么不同?
2.与二元一次方程 3x+2y=120相比,有什么不同?
5x+4y=210
未知数最高次数为2
{
只有一个未知数
3.与分式方程 相比,有什么不同?
未知数没有在分母位置,是整式方程
一元二次方程
叫什么方程合适呢?
获取新知
一起探究
我们来研究一下方程2(1+x)2=2.42的特点
注意关键点
1.一元
2.二次
3.整式
定义:只含有一个未知数,并且未知数的最高次数为2的整式方程,叫做一元二次方程.
一元二次方程的一般形式
a x 2 + b x + c = 0(a≠0)
二次项系数
一次项系数
常数项
二次项
一次项
常数项
思考:为什么要有限制条件a≠0
若a=0,则没有了二次项,也就不是二次方程了.
指出方程各项的系数时要带上前面的符号.
例1 将方程3x(x-1)=5(x+2)化为一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
解: 去括号,得
其中二次项系数为3,一次项系数为-8,常数项为-10.
3x2-3x=5x+10.
移项,合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
例题讲解
获取新知
问题:类比一元一次方程,试着归纳一元二次方程根的定义.
一元一次方程的根:
使一元一次方程 的未知数的值叫做一元一次方程的解,也叫一元一次方程的根.
左右两边相等
定义: 使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解,也叫一元二次方程的根.
例题讲解
例2 判断0和-1是不是一元二次方程2x2=1-x的根.
当x=0时,左边=0,右边=1
左边≠右边
∴0不是原方程的根.
解:
当x=-1时,左边=2,右边=2
左边=右边
∴-1是原方程的根.
判断一个数值是不是一元二次方程的根的方法:
将这个值代入一元二次方程,看方程的左右两边是否相等,若相等,则是方程的根;若不相等,就不是方程的根.
例3 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛.如图要使花坛的总面积为570m2,问小路的宽应为多少?
32
20
x
思考:
1.若设小路的宽是xm,那么横向小路的面积是_____m2,纵向小路的面积是 m2,两者重叠的面积是 m2.
32x
2×20x
2x2
2.由于花坛的总面积是570m2.你能根据题意,列出方程吗?
32×20-(32x+2×20x)+2x2=570
整理以上方程可得:
x2-36x+35=0
1. 下列哪些是一元二次方程?
(1)3x+2=5x-2
(2)x2=0
(3)(x+3)(2x-4)=x2
(4)3y2=(3y+1)(y-2)
(5)x2=x3+x2-1
(6)3x2=5x-1
随堂演练
2.填空:
方程 一般形式 二次项系数 一次项系数 常数项
-2
1
3
1
3
-5
4
0
-5
3
-2
3.如图,有一张矩形纸片,长10 cm,宽 6 cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面面积是 32 cm2,求剪去的小正方形的边长.设剪去的小正方形的边长是 x cm,根据题意可列方程为( )
A.10×6-4×6x=32
B.(10-2x)(6-2x)=32
C.(10-x)(6-x)=32
D.10×6-4x2=32
B
4.根据下列问题列方程,并将所列方程化成一元二次方程的一般形式:
(1)一个圆的面积是 6.28 cm2,求半径;
(2)一个直角三角形的两条直角边相差 3 cm,面积是 9 cm2,求较长的直角边.
解:(1)设圆的半径为rcm,则圆的面积为(πr2)cm2,
所以其一般形式为πr2-6.28=0.
(2)设较长的直角边长为acm,则较短的直角边长为(a-3)cm,
则直角三角形的面积为 cm2
所以其一般形式为a2-3a-18=0.
5.如果 2 是方程 x2-c=0 的一个根,那么常数 c 是多少?求出这个方程的其他根.
解:因为 2 是方程 x2-c=0 的一个根,
所以 22-c=0,
解得 c=4,
则原方程为 x2-4=0,即x2=4,
因为 4 的平方根为±2,
所以方程 x2-4=0 的另一个根为-2.
课堂小结
是整式方程
一元二次方程
只含有一个未知数
未知数的最高次数是2
ax2+bx+c=0(a≠0)
一元二次方程的概念
一元二次方程的一般形式
一元二次方程的解(根)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
