冀教版数学九年级上册同步课件:24.2 第3课时 因式分解法 课件(共22张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:24.2 第3课时 因式分解法 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 13:51:40 | ||
图片预览





文档简介
(共22张PPT)
第二十四章 一元一次方程
24.2 第3课时 因式分解法
知识回顾
复习:因式分解的方法
提公因式法
公式法
一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法.
利用平方差公式a2-b2= (a+b)(a-b)
和完全平方公式a2±2ab+b2=(a±b)2分解因式.
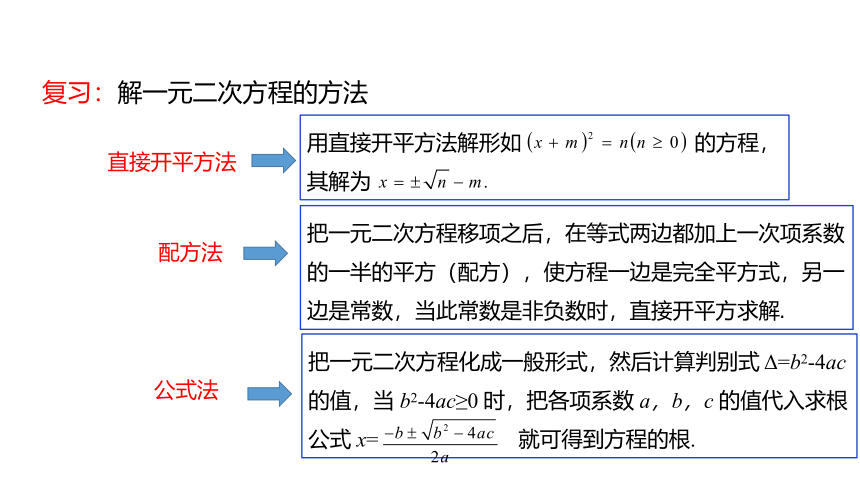
复习:解一元二次方程的方法
直接开平方法
公式法
用直接开平方法解形如 的方程,
其解为
配方法
把一元二次方程移项之后,在等式两边都加上一次项系数的一半的平方(配方),使方程一边是完全平方式,另一边是常数,当此常数是非负数时,直接开平方求解.
把一元二次方程化成一般形式,然后计算判别式 Δ=b2-4ac 的值,当 b2-4ac≥0 时,把各项系数 a,b,c 的值代入求根公式 x= 就可得到方程的根.
情景导入
根据物理学规律,如果把一个物体从地面以10 m/s的速度竖直上抛,那么物体经过x s离地面的高度(单位:m)为
10x-4.9x2.
根据上述规律,物体经过多少秒落回地面(结果保留小数点后两位)?
设物体经过x s落回地面,这时它离地面的高度为0 m,
即 10x-4.9x2=0. ①
除配方法或公式法以外,能否找到更简单的方法解方程①?
因式分解
如果a · b = 0,
那么a = 0或 b = 0.
两个因式乘积为 0,说明什么?
或
降次,化为两个一次方程
解两个一次方程,得出原方程的根
10x-4.9x2 =0
x(10-4.9x) =0
x =0
10-4.9x=0
获取新知
一起探究
这种通过因式分解,将一个一元二次方程转化为两个一元一次方程来求解的方法叫做因式分解法.
因式分解法的概念
因式分解法的基本步骤
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
简记歌诀:
右化零 左分解
两因式 各求解
例1.用因式分解法解下列方程:
(1)3(x-1)2=2(x-1)
解:原方程可化为
3(x-1)2-2(x-1)=0
(x-1)[3(x-1)-2]=0
即(x-1)(3x-5)=0
∴x-1=0,或3x-5=0
①利用移项,将方程右边化为0
②在方程的左边分解因式
③化简分解后的因式
④转化为两个一次方程
⑤得出方程的解
(先独立完成,再与43页例题比照)
例题讲解
(2)4(x-2)2=(x-1)2
解:原方程可化为
4(x-2)2-(x-1)2=0
即(2x-4)2-(x-1)2=0
∴(2x-4+x-1)(2x-4-x+1)=0
(3x-5)(x-3)=0
∴3x-5=0,或x-3=0
4进到括号里,可使计算方便
分解后,化简因式,可使计算方便
你还会用其他方法做吗?
(2)4(x-2)2=(x-1)2
解:直接开平方,得
2(x-2)=±(x-1)
∴2(x-2)=x-1,或2(x-2)=-(x-1)
等号的两边均为平方形式时,直接开平方法也是一种很好的方法.
总结提升
因式分解法,只适合一些特殊的一元二次方程.即当把方程的所有项移到等号左边的时候,方程的左边可以分解因式.并不是所有的一元二次方程都能用因式分解法去解.
思考:任何方程都可以用因式分解法解吗?
先选择合适的解法,再解方程.
① x2+2x=3
② x2-3x=5(x-3)
③ 3x2-2x-2=0
④(3x+2)2=25
直接开平方法
配方法
公式法
因式分解法
思考:解一元二次方程如何选择适当的解法?与你的同伴交流一下吧.
例2 用适当的方法解方程:
(1) 3x(x + 5)= 5(x + 5); (2)(5x + 1)2 = 1;
解: 3x(x + 5)- 5(x + 5)=0
(3x -5) (x + 5) = 0.
即 3x - 5 = 0 或 x + 5 = 0.
解:开平方,得
5x + 1 = ±1.
解得, x 1= 0 , x2=
【分析】该式左右两边可以提取公因式,所以用因式分解法解答较快.
【分析】方程一边以平方形式出现,另一边是常数,可直接开平方法.
(3)x2 - 12x = 4 ; (4)3x2 = 4x + 1;
解:配方,得
x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
解得
x1= , x2=
解:化为一般形式
3x2 - 4x + 1 = 0.
∵Δ=b2 - 4ac = 28 > 0,
【分析】二次项的系数为1,可用配方法来解题较快.
【分析】二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
获取新知
常见的可以用因式分解法求解的方程的类型:
常见类型 因式分解 方程的解
x2+bx=0 x(x+b)=0 x1=0,x2=-b
x2-a2=0 (x+a)(x-a)=0 x1=-a,x2=a
x2±2ax+a2 (x±a)2=0 x1=x2= a
x2+(a+b)x+ab (a,b为常数) (x+a)(x+b)=0 x1=-a,x2=-b
一元二次方程解法的比较
方法 理论依据 方程类型 关键步骤 主要特点
直接开平方 平方根的定义 (ax+b)2=n(a≠0,n≥0) 开平方 求解迅速、准确,使用类型限制
配方法 完全平方公式 所有 配方 步骤繁琐,当二次项系数是1和一次项系数是偶数时较适用
公式法 配方 所有 代入求根公式 计算量大,易出现符号问题
因式分解法 若ab=0,则a=0或b=0 ab=0 分解因式 求解迅速、准确,适用面较小
随堂演练
①x2-3x+1=0 ; ②3x2-1=0 ; ③ -3t2+t=0 ;
④x2-4x=2 ; ⑤2x2-x=0; ⑥ 5(m+2)2=8;
⑦ 3y2-y-1=0; ⑧ 2x2+4x-1=0;⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
1.填空
⑥
②
③
⑤
⑨
①
⑦
⑧
④
2.解方程(x+2)2=3(2+x),最适当的解法是( )
A.直接开平方法
B.配方法
C.公式法
D.因式分解法
D
3.用因式分解法解下列方程:
(1) 3x2-12x=-12; (2) 3x(x-1)=2(x-1).
解:(1) 方程整理为 x2-4x+4=0,
(x-2)2=0,
所以 x1=x2=2.
(2) 方程整理为 3x(x-1)-2(x-1)=0,
(x-1)(3x-2)=0,
x-1=0或3x-2=0,
所以 x1=1, .
4.用合适的方法解下列一元二次方程:
(1) 3x(x + 5)= 5(x + 5); (2)(5x + 1)2 = 1;
解:化简 (3x -5) (x + 5) = 0.
即 3x - 5 = 0 或 x + 5 = 0.
解:开平方,得
5x + 1 = ±1.
解得, x 1= 0 , x2=
(3)x2 - 12x = 4 ; (4)3x2 = 4x + 1;
解:化为一般形式
3x2 - 4x + 1 = 0.
∵Δ=b2 - 4ac = 28 > 0,
解:配方,得
x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
解得
5.把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,求小圆形场地的半径.
解:设小圆形场地的半径为r,
根据题意 ( r + 5 )2×π=2r2π.
因式分解,得
于是得
答:小圆形场地的半径是
课堂小结
因式分解法
步骤
概念
原理
将方程左边因式分解,右边=0.
因式分解的方法有
ma + mb + mc = m(a+ b+ c);
a2 ±2ab+b2=(a ± b)2;
a2 -b2=(a + b)(a-b).
如果 a · b =0,那么a=0或b=0.
简记歌诀:
右化零 左分解
两因式 各求解
第二十四章 一元一次方程
24.2 第3课时 因式分解法
知识回顾
复习:因式分解的方法
提公因式法
公式法
一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法.
利用平方差公式a2-b2= (a+b)(a-b)
和完全平方公式a2±2ab+b2=(a±b)2分解因式.
复习:解一元二次方程的方法
直接开平方法
公式法
用直接开平方法解形如 的方程,
其解为
配方法
把一元二次方程移项之后,在等式两边都加上一次项系数的一半的平方(配方),使方程一边是完全平方式,另一边是常数,当此常数是非负数时,直接开平方求解.
把一元二次方程化成一般形式,然后计算判别式 Δ=b2-4ac 的值,当 b2-4ac≥0 时,把各项系数 a,b,c 的值代入求根公式 x= 就可得到方程的根.
情景导入
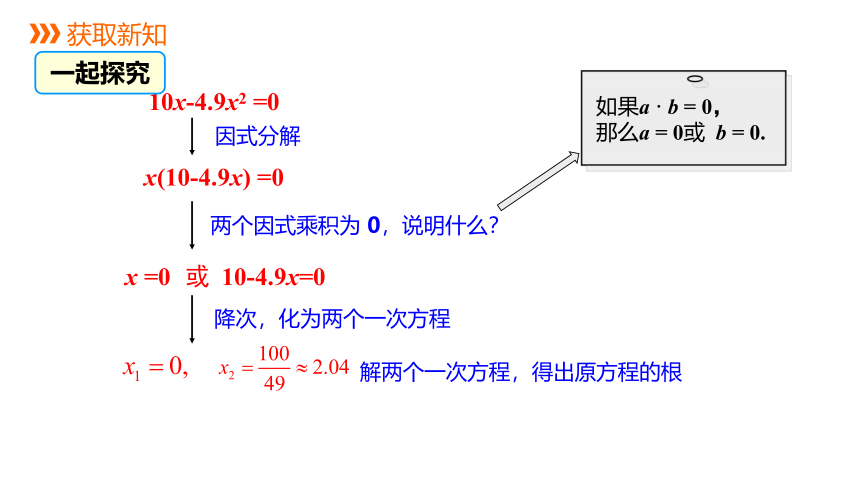
根据物理学规律,如果把一个物体从地面以10 m/s的速度竖直上抛,那么物体经过x s离地面的高度(单位:m)为
10x-4.9x2.
根据上述规律,物体经过多少秒落回地面(结果保留小数点后两位)?
设物体经过x s落回地面,这时它离地面的高度为0 m,
即 10x-4.9x2=0. ①
除配方法或公式法以外,能否找到更简单的方法解方程①?
因式分解
如果a · b = 0,
那么a = 0或 b = 0.
两个因式乘积为 0,说明什么?
或
降次,化为两个一次方程
解两个一次方程,得出原方程的根
10x-4.9x2 =0
x(10-4.9x) =0
x =0
10-4.9x=0
获取新知
一起探究
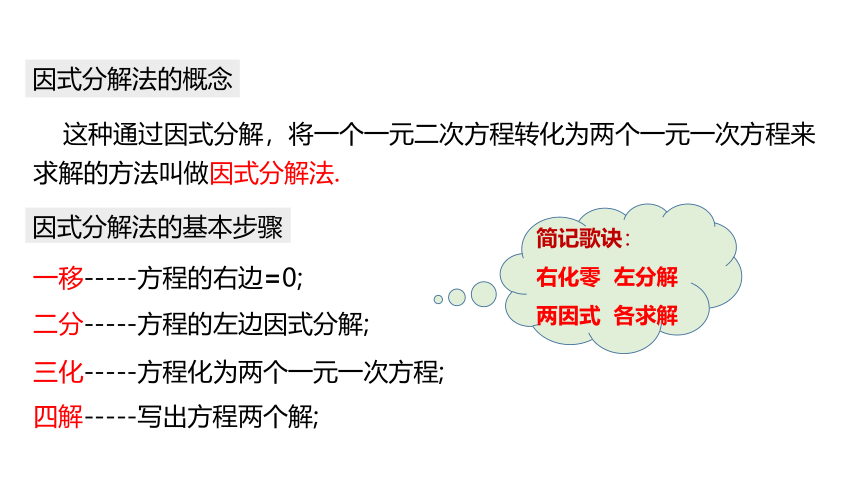
这种通过因式分解,将一个一元二次方程转化为两个一元一次方程来求解的方法叫做因式分解法.
因式分解法的概念
因式分解法的基本步骤
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
简记歌诀:
右化零 左分解
两因式 各求解
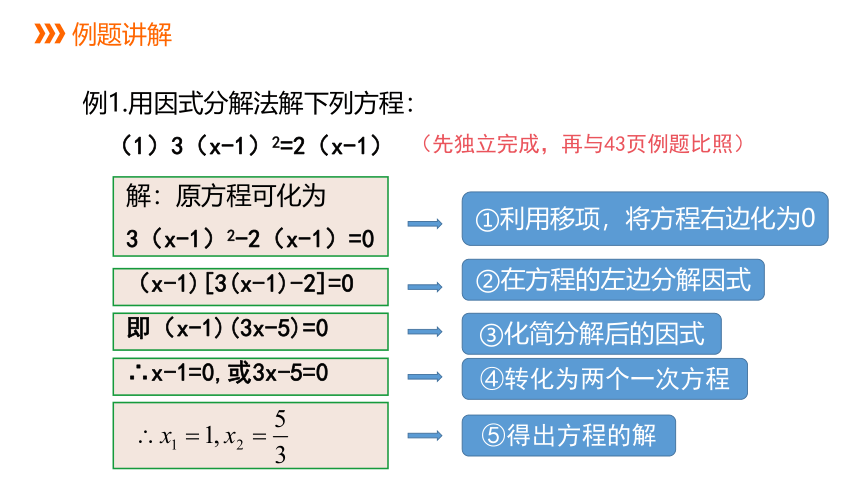
例1.用因式分解法解下列方程:
(1)3(x-1)2=2(x-1)
解:原方程可化为
3(x-1)2-2(x-1)=0
(x-1)[3(x-1)-2]=0
即(x-1)(3x-5)=0
∴x-1=0,或3x-5=0
①利用移项,将方程右边化为0
②在方程的左边分解因式
③化简分解后的因式
④转化为两个一次方程
⑤得出方程的解
(先独立完成,再与43页例题比照)
例题讲解
(2)4(x-2)2=(x-1)2
解:原方程可化为
4(x-2)2-(x-1)2=0
即(2x-4)2-(x-1)2=0
∴(2x-4+x-1)(2x-4-x+1)=0
(3x-5)(x-3)=0
∴3x-5=0,或x-3=0
4进到括号里,可使计算方便
分解后,化简因式,可使计算方便
你还会用其他方法做吗?
(2)4(x-2)2=(x-1)2
解:直接开平方,得
2(x-2)=±(x-1)
∴2(x-2)=x-1,或2(x-2)=-(x-1)
等号的两边均为平方形式时,直接开平方法也是一种很好的方法.
总结提升
因式分解法,只适合一些特殊的一元二次方程.即当把方程的所有项移到等号左边的时候,方程的左边可以分解因式.并不是所有的一元二次方程都能用因式分解法去解.
思考:任何方程都可以用因式分解法解吗?
先选择合适的解法,再解方程.
① x2+2x=3
② x2-3x=5(x-3)
③ 3x2-2x-2=0
④(3x+2)2=25
直接开平方法
配方法
公式法
因式分解法
思考:解一元二次方程如何选择适当的解法?与你的同伴交流一下吧.
例2 用适当的方法解方程:
(1) 3x(x + 5)= 5(x + 5); (2)(5x + 1)2 = 1;
解: 3x(x + 5)- 5(x + 5)=0
(3x -5) (x + 5) = 0.
即 3x - 5 = 0 或 x + 5 = 0.
解:开平方,得
5x + 1 = ±1.
解得, x 1= 0 , x2=
【分析】该式左右两边可以提取公因式,所以用因式分解法解答较快.
【分析】方程一边以平方形式出现,另一边是常数,可直接开平方法.
(3)x2 - 12x = 4 ; (4)3x2 = 4x + 1;
解:配方,得
x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
解得
x1= , x2=
解:化为一般形式
3x2 - 4x + 1 = 0.
∵Δ=b2 - 4ac = 28 > 0,
【分析】二次项的系数为1,可用配方法来解题较快.
【分析】二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
获取新知
常见的可以用因式分解法求解的方程的类型:
常见类型 因式分解 方程的解
x2+bx=0 x(x+b)=0 x1=0,x2=-b
x2-a2=0 (x+a)(x-a)=0 x1=-a,x2=a
x2±2ax+a2 (x±a)2=0 x1=x2= a
x2+(a+b)x+ab (a,b为常数) (x+a)(x+b)=0 x1=-a,x2=-b
一元二次方程解法的比较
方法 理论依据 方程类型 关键步骤 主要特点
直接开平方 平方根的定义 (ax+b)2=n(a≠0,n≥0) 开平方 求解迅速、准确,使用类型限制
配方法 完全平方公式 所有 配方 步骤繁琐,当二次项系数是1和一次项系数是偶数时较适用
公式法 配方 所有 代入求根公式 计算量大,易出现符号问题
因式分解法 若ab=0,则a=0或b=0 ab=0 分解因式 求解迅速、准确,适用面较小
随堂演练
①x2-3x+1=0 ; ②3x2-1=0 ; ③ -3t2+t=0 ;
④x2-4x=2 ; ⑤2x2-x=0; ⑥ 5(m+2)2=8;
⑦ 3y2-y-1=0; ⑧ 2x2+4x-1=0;⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
1.填空
⑥
②
③
⑤
⑨
①
⑦
⑧
④
2.解方程(x+2)2=3(2+x),最适当的解法是( )
A.直接开平方法
B.配方法
C.公式法
D.因式分解法
D
3.用因式分解法解下列方程:
(1) 3x2-12x=-12; (2) 3x(x-1)=2(x-1).
解:(1) 方程整理为 x2-4x+4=0,
(x-2)2=0,
所以 x1=x2=2.
(2) 方程整理为 3x(x-1)-2(x-1)=0,
(x-1)(3x-2)=0,
x-1=0或3x-2=0,
所以 x1=1, .
4.用合适的方法解下列一元二次方程:
(1) 3x(x + 5)= 5(x + 5); (2)(5x + 1)2 = 1;
解:化简 (3x -5) (x + 5) = 0.
即 3x - 5 = 0 或 x + 5 = 0.
解:开平方,得
5x + 1 = ±1.
解得, x 1= 0 , x2=
(3)x2 - 12x = 4 ; (4)3x2 = 4x + 1;
解:化为一般形式
3x2 - 4x + 1 = 0.
∵Δ=b2 - 4ac = 28 > 0,
解:配方,得
x2 - 12x + 62 = 4 + 62,
即 (x - 6)2 = 40.
开平方,得
解得
5.把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,求小圆形场地的半径.
解:设小圆形场地的半径为r,
根据题意 ( r + 5 )2×π=2r2π.
因式分解,得
于是得
答:小圆形场地的半径是
课堂小结
因式分解法
步骤
概念
原理
将方程左边因式分解,右边=0.
因式分解的方法有
ma + mb + mc = m(a+ b+ c);
a2 ±2ab+b2=(a ± b)2;
a2 -b2=(a + b)(a-b).
如果 a · b =0,那么a=0或b=0.
简记歌诀:
右化零 左分解
两因式 各求解
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
