冀教版数学九年级上册同步课件:24.2 第1课时 配方法(共25张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:24.2 第1课时 配方法(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 385.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:03:39 | ||
图片预览







文档简介
(共25张PPT)
第二十四章 一元二次方程
24.2 第1课时 配方法
知识回顾
(1)121的平方根为±11;
(2)25的平方根为±5;
(3)0.81的平方根为±0.9;
(4)0的平方根为0;
1.求出或表示出下列各数的平方根.
121; (2) 25 ; (3) 0.81;
(4) 0; (5) 3; (6) .
(5)3的平方根为 ;
(6) 的平方根为 ;
2.一个正数4有( )个平方根,是( ).
0有( )个平方根,是( ).
负数-4( )平方根.
2
±2
1
0
没有
是学习新知的必备条件哦
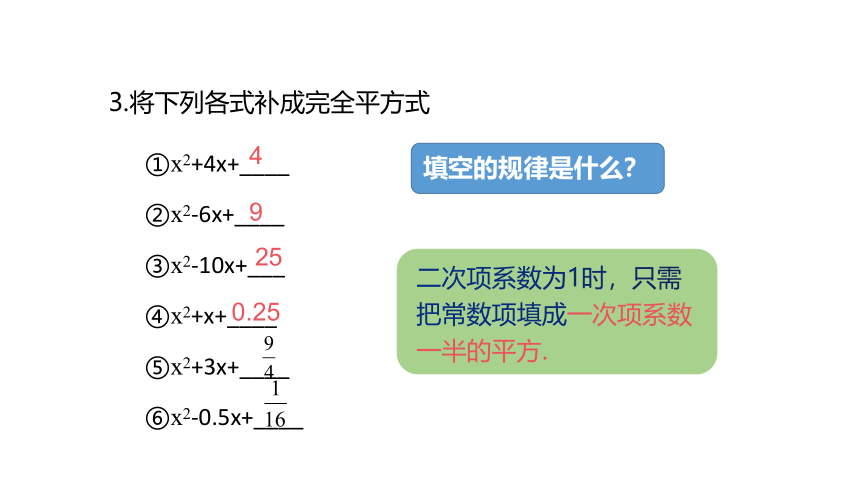
3.将下列各式补成完全平方式
①x2+4x+____
②x2-6x+____
③x2-10x+___
④x2+x+____
⑤x2+3x+____
⑥x2-0.5x+____
4
9
25
0.25
填空的规律是什么?
二次项系数为1时,只需把常数项填成一次项系数一半的平方.
情景导入
一桶油漆可刷的面积为1 500 dm2,李林用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
解:设盒子的棱长为x dm,则这个盒子的表面积为 6x2 dm2,根据一桶油漆可刷的面积,列出方程
10×6x2=1 500,
由此可得
x2=25,①
即
x1=5,x2= 5.
可以验证,因为棱长不能是负值,
所以盒子的棱长为5 dm.
用方程解决实际问题时,要考虑所得结果是否符合实际意义
获取新知
分类思想
知识点1 用直接开平方法解一元二次方程
(2)当p=0时,方程(Ⅰ)有两个相等的实数根 .
(3)当p<0时,因为对任何实数x,都有x2≥0 ,所以方程(Ⅰ)无实数根.
一般的,对于方程 x2 = p, (Ⅰ)
(1)当p>0时,根据平方根的意义,方程(Ⅰ)有两个不等的
实数根
例题讲解
例1 利用直接开平方法解下列方程:
(1) x2=6;
(2) x2-900=0.
解:
(1) x2=6,
直接开平方,得
(2)移项,得
x2=900.
直接开平方,得
x=±30,
∴x1=30, x2=-30.
获取新知
知识点2 解形式为 (x+m)2=n (其中m,n 是常数)的一元二次方程
解方程:(x + 3)2 = 5时,由方程 x2 =25 得 x =±5.由此想到:由方程
(x + 3)2 = 5, ①
整体思想
得 x + 3 = ,
一元二次方程
降次
转化思想
一元一次方程
即 x + 3 = ,或x + 3 = ②
于是,方程(x + 3)2 = 5的两个根为x1=-3+ ,x2=-3-
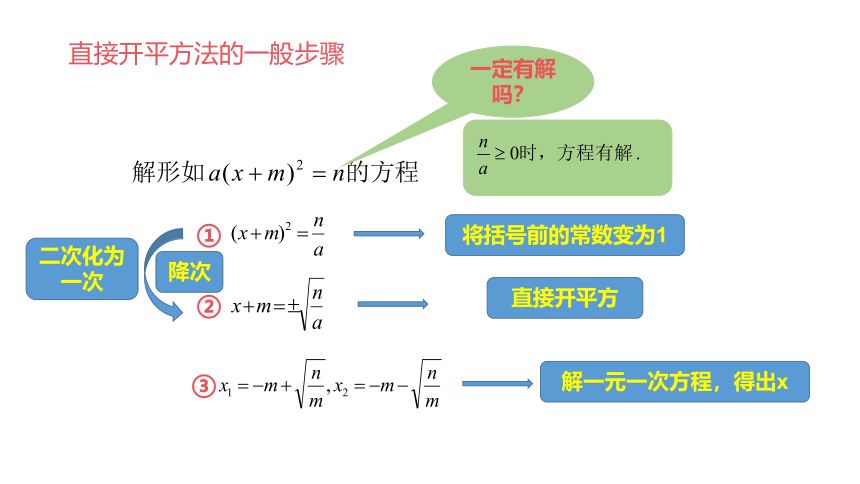
直接开平方法的一般步骤
①
②
③
将括号前的常数变为1
直接开平方
解一元一次方程,得出x
二次化为一次
降次
一定有解吗?
例题讲解
例2 解下列方程:
⑴ (x+1)2= 2 ;
(2)(x-1)2-4 = 0;
【分析】第1小题中只要将(x+1)看成是一个整体,就可以运用直接开平方法求解;第2小题先将-4移到方程的右边,再同第1小题一样地解.
解:(1)∵x+1是2的平方根,
∴x+1=
即x1=-1+
,x2=-1-
(2)移项,得(x-1)2=4.
∵x-1是4的平方根,
∴x-1=±2.
即x1=3,x2=-1.
获取新知
知识点3 配方法解二次项系数为1的一元二次方程
根据完全平方公式:a2±2ab+b2=(a±b)2
完成填空: (1) x2–4x+____=(x–____)2
(2) x2+12x+____=(x+____)2
(3) y2–8y+____=(y–____)2
思考:你所填写的 b,b2 与一次项的系数有怎样的关系?
二次项系数为 1 的完全平方式:常数项等于一次项系数一半的平方
探究用配方法解一元二次方程
解方程 (1) x2-2x+1=4
能转化为你会做的形式吗?
原方程可化为(x-1)2=4
(x-1)2
用直接开平方法即可
解方程 (2) x2-2x=3
分析:能转化为(1)吗?
方程两边同时加1即可
x2-2x+1=3+1
转化为(1) x2-2x+1=4
怎样解方程 x2 + 6x + 4=0?
移项
x2 + 6x= – 4
两边加 9
x2 + 6x + 9= – 4 + 9
左边写成完全平方形式
(x + 3)2= 5
解得
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方
配方法
1.概念:通过配方,把一元二次方程变形为一边含未知数的一次式的平方,另一边为常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个一元一次方程,从而求出原方程的根.这种解一元二次方程的方法叫做配方法.
注意:由于配方法是通过变形,将一元二次方程最终转化为用直接开平方去解,因此用配方法解一元二次方程也会出现3种结果.即方程有两个不相等的根;或一个根;或没有根.
例题讲解
例3 用配方法解下列方程.
(1)x2-10x-11=0; (2)x2+2x-1=0.
解:(1)移项,得
x2-10x=11.
配方,得
x2-10x+52=11+52,
即 (x-5)2=36.
两边开方,得
所以 x1=11,x2=-1
(2)移项,得x2+2x=1.
配方,得
x2+2x+12=1+12,
即 (x+1)2=2.
两边开方,得
所以
获取新知
知识点4 配方法解二次项系数不为1的一元二次方程
问题:如何用配方法解方程2x2+4x+1=0?
提示:如果方程的系数不是1,我们可以在方程的两边同时除以二次项系数,这样转化为系数是1的方程,就可以利用学过的知识解方程了!
解:移项,并将二次项系数化为1,得 .
配方,得 ,即 .
两边开平方,得 .
所以 , .
用配方法解一元二次方程的一般步骤:
例题讲解
例4 用配方法解方程:2x2+3=6x.
解:(1)移项,并将二次项系数化为1,得
x2-3x=
配方,得x2-3x+
即
两边开方,得
所以
随堂演练
1.若代数式3x2-6的值是21,则x的值是( )
A.3 B.±3
C.-3 D.±
B
2.已知关于x的方程ax2=b的两根分别为m-1和2m+7,则方程的两根为( )
A.±2 B.±3
C.±4 D.±7
B
3.若x2-4x+p=(x+q)2,则p,q的值分别是( )
A.p=4,q=2 B.p=4,q=-2
C.p=-4,q=2 D.p=-4,q=-2
B
4.若方程4x2-(m-2)x+1=0的左边是一个完全平方式,则m等于( )
A.-2 B.-2或6 C.-2或-6 D.2或-6
B
5.解下列方程:
(1)x2-2x-1=0; (2)3x2-6x+4=0.
解:(1)移项,得x2-2x=1.
配方,得x2-2x+12=1+12,
即(x-1)2=2.
两边开平方,得x-1= ,
所以x1=1+ ,x2=1- .
(2)移项,得3x2 -6x=-4.
二次项的系数化为1,得
x2 -2x = .
配方,得x2-2x+12= +12.
即(x-1)2= .
因为实数的平方都是非负数,所以上式都不成立,即原方程无实根.
6.试用配方法说明:不论k取何实数,多项式k2-4k+5 的值必定大于零.
解:k2-4k+5=k2-4k+4-4+5
=(k-2)2+1
因为(k-2)2≥0,
所以(k-2)2+1≥1.
所以k2-4k+5的值必定大于零.
课堂小结
一元二次方程的解法(1)
基本思路
配方法
特征
直接开平方法
概念
定义
可化为x2=p或(x+n)2= p(p≥0)的形式
步骤
移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.
第二十四章 一元二次方程
24.2 第1课时 配方法
知识回顾
(1)121的平方根为±11;
(2)25的平方根为±5;
(3)0.81的平方根为±0.9;
(4)0的平方根为0;
1.求出或表示出下列各数的平方根.
121; (2) 25 ; (3) 0.81;
(4) 0; (5) 3; (6) .
(5)3的平方根为 ;
(6) 的平方根为 ;
2.一个正数4有( )个平方根,是( ).
0有( )个平方根,是( ).
负数-4( )平方根.
2
±2
1
0
没有
是学习新知的必备条件哦
3.将下列各式补成完全平方式
①x2+4x+____
②x2-6x+____
③x2-10x+___
④x2+x+____
⑤x2+3x+____
⑥x2-0.5x+____
4
9
25
0.25
填空的规律是什么?
二次项系数为1时,只需把常数项填成一次项系数一半的平方.
情景导入
一桶油漆可刷的面积为1 500 dm2,李林用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
解:设盒子的棱长为x dm,则这个盒子的表面积为 6x2 dm2,根据一桶油漆可刷的面积,列出方程
10×6x2=1 500,
由此可得
x2=25,①
即
x1=5,x2= 5.
可以验证,因为棱长不能是负值,
所以盒子的棱长为5 dm.
用方程解决实际问题时,要考虑所得结果是否符合实际意义
获取新知
分类思想
知识点1 用直接开平方法解一元二次方程
(2)当p=0时,方程(Ⅰ)有两个相等的实数根 .
(3)当p<0时,因为对任何实数x,都有x2≥0 ,所以方程(Ⅰ)无实数根.
一般的,对于方程 x2 = p, (Ⅰ)
(1)当p>0时,根据平方根的意义,方程(Ⅰ)有两个不等的
实数根
例题讲解
例1 利用直接开平方法解下列方程:
(1) x2=6;
(2) x2-900=0.
解:
(1) x2=6,
直接开平方,得
(2)移项,得
x2=900.
直接开平方,得
x=±30,
∴x1=30, x2=-30.
获取新知
知识点2 解形式为 (x+m)2=n (其中m,n 是常数)的一元二次方程
解方程:(x + 3)2 = 5时,由方程 x2 =25 得 x =±5.由此想到:由方程
(x + 3)2 = 5, ①
整体思想
得 x + 3 = ,
一元二次方程
降次
转化思想
一元一次方程
即 x + 3 = ,或x + 3 = ②
于是,方程(x + 3)2 = 5的两个根为x1=-3+ ,x2=-3-
直接开平方法的一般步骤
①
②
③
将括号前的常数变为1
直接开平方
解一元一次方程,得出x
二次化为一次
降次
一定有解吗?
例题讲解
例2 解下列方程:
⑴ (x+1)2= 2 ;
(2)(x-1)2-4 = 0;
【分析】第1小题中只要将(x+1)看成是一个整体,就可以运用直接开平方法求解;第2小题先将-4移到方程的右边,再同第1小题一样地解.
解:(1)∵x+1是2的平方根,
∴x+1=
即x1=-1+
,x2=-1-
(2)移项,得(x-1)2=4.
∵x-1是4的平方根,
∴x-1=±2.
即x1=3,x2=-1.
获取新知
知识点3 配方法解二次项系数为1的一元二次方程
根据完全平方公式:a2±2ab+b2=(a±b)2
完成填空: (1) x2–4x+____=(x–____)2
(2) x2+12x+____=(x+____)2
(3) y2–8y+____=(y–____)2
思考:你所填写的 b,b2 与一次项的系数有怎样的关系?
二次项系数为 1 的完全平方式:常数项等于一次项系数一半的平方
探究用配方法解一元二次方程
解方程 (1) x2-2x+1=4
能转化为你会做的形式吗?
原方程可化为(x-1)2=4
(x-1)2
用直接开平方法即可
解方程 (2) x2-2x=3
分析:能转化为(1)吗?
方程两边同时加1即可
x2-2x+1=3+1
转化为(1) x2-2x+1=4
怎样解方程 x2 + 6x + 4=0?
移项
x2 + 6x= – 4
两边加 9
x2 + 6x + 9= – 4 + 9
左边写成完全平方形式
(x + 3)2= 5
解得
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方
配方法
1.概念:通过配方,把一元二次方程变形为一边含未知数的一次式的平方,另一边为常数,当常数为非负数时,利用开平方,将一元二次方程转化为两个一元一次方程,从而求出原方程的根.这种解一元二次方程的方法叫做配方法.
注意:由于配方法是通过变形,将一元二次方程最终转化为用直接开平方去解,因此用配方法解一元二次方程也会出现3种结果.即方程有两个不相等的根;或一个根;或没有根.
例题讲解
例3 用配方法解下列方程.
(1)x2-10x-11=0; (2)x2+2x-1=0.
解:(1)移项,得
x2-10x=11.
配方,得
x2-10x+52=11+52,
即 (x-5)2=36.
两边开方,得
所以 x1=11,x2=-1
(2)移项,得x2+2x=1.
配方,得
x2+2x+12=1+12,
即 (x+1)2=2.
两边开方,得
所以
获取新知
知识点4 配方法解二次项系数不为1的一元二次方程
问题:如何用配方法解方程2x2+4x+1=0?
提示:如果方程的系数不是1,我们可以在方程的两边同时除以二次项系数,这样转化为系数是1的方程,就可以利用学过的知识解方程了!
解:移项,并将二次项系数化为1,得 .
配方,得 ,即 .
两边开平方,得 .
所以 , .
用配方法解一元二次方程的一般步骤:
例题讲解
例4 用配方法解方程:2x2+3=6x.
解:(1)移项,并将二次项系数化为1,得
x2-3x=
配方,得x2-3x+
即
两边开方,得
所以
随堂演练
1.若代数式3x2-6的值是21,则x的值是( )
A.3 B.±3
C.-3 D.±
B
2.已知关于x的方程ax2=b的两根分别为m-1和2m+7,则方程的两根为( )
A.±2 B.±3
C.±4 D.±7
B
3.若x2-4x+p=(x+q)2,则p,q的值分别是( )
A.p=4,q=2 B.p=4,q=-2
C.p=-4,q=2 D.p=-4,q=-2
B
4.若方程4x2-(m-2)x+1=0的左边是一个完全平方式,则m等于( )
A.-2 B.-2或6 C.-2或-6 D.2或-6
B
5.解下列方程:
(1)x2-2x-1=0; (2)3x2-6x+4=0.
解:(1)移项,得x2-2x=1.
配方,得x2-2x+12=1+12,
即(x-1)2=2.
两边开平方,得x-1= ,
所以x1=1+ ,x2=1- .
(2)移项,得3x2 -6x=-4.
二次项的系数化为1,得
x2 -2x = .
配方,得x2-2x+12= +12.
即(x-1)2= .
因为实数的平方都是非负数,所以上式都不成立,即原方程无实根.
6.试用配方法说明:不论k取何实数,多项式k2-4k+5 的值必定大于零.
解:k2-4k+5=k2-4k+4-4+5
=(k-2)2+1
因为(k-2)2≥0,
所以(k-2)2+1≥1.
所以k2-4k+5的值必定大于零.
课堂小结
一元二次方程的解法(1)
基本思路
配方法
特征
直接开平方法
概念
定义
可化为x2=p或(x+n)2= p(p≥0)的形式
步骤
移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
