冀教版数学九年级上册同步课件:25.2 第1课时 平行线分线段成比例(共21张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:25.2 第1课时 平行线分线段成比例(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 463.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 15:12:18 | ||
图片预览





文档简介
(共21张PPT)
第二十五章 图形的相似
25.2 第1课时 平行线分线段成比例
1.什么是线段的比
2.什么是成比例线段
3.你能不通过测量快速将一根绳子分成两部分,
使得这两部分的比是2 ∶ 3
知识回顾
复习
观察与思考
下图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
A1B1=B1C1,
情景导入
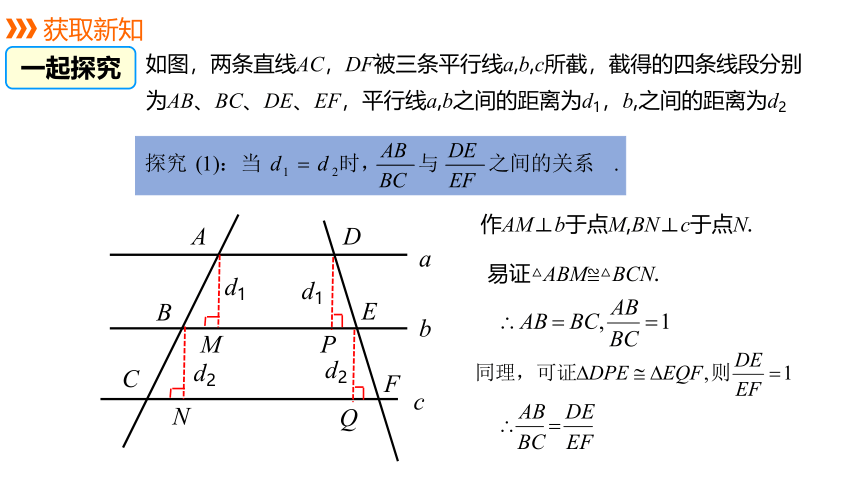
如图,两条直线AC,DF被三条平行线a,b,c所截,截得的四条线段分别为AB、BC、DE、EF,平行线a,b之间的距离为d1,b,之间的距离为d2
a
b
c
A
B
C
D
E
F
Q
P
N
M
作AM⊥b于点M,BN⊥c于点N.
易证△ABM≌△BCN.
获取新知
一起探究
d1
d1
d2
d2
a
b
c
A
B
C
D
E
F
G
H
M
N
P
Q
由探究(1)的结论可得,AG=GB=BH=HM=MC,
DN=NE=EP=PQ=QF
a
b
c
A
B
C
D
E
F
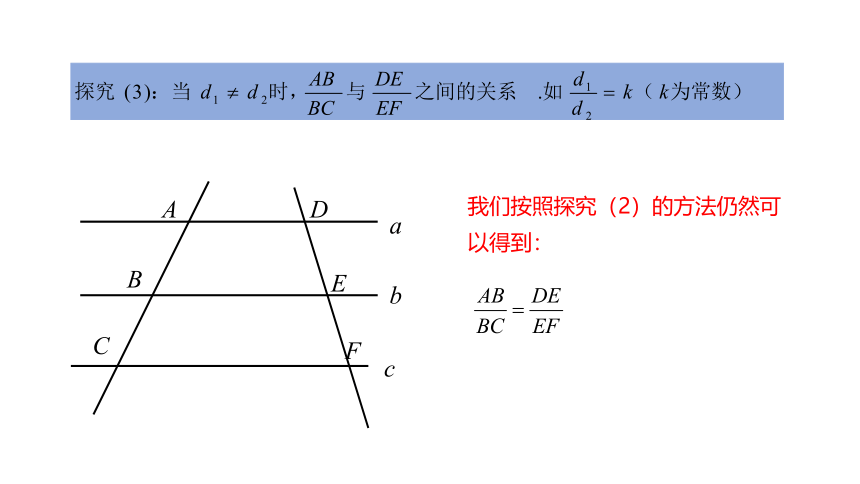
我们按照探究(2)的方法仍然可以得到:
一、基本事实:两条直线被一组平行线所截,截得的
对应线段成比例.
a
b
c
A
B
C
D
E
F
几何语言:
∵a//b//c
一般指三条平行线
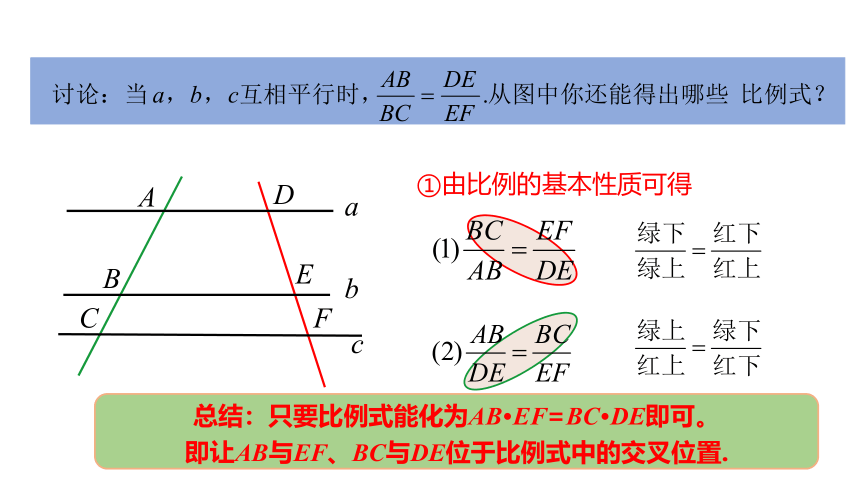
①由比例的基本性质可得
总结:只要比例式能化为AB·EF=BC·DE即可。
即让AB与EF、BC与DE位于比例式中的交叉位置.
a
b
c
A
B
C
D
E
F
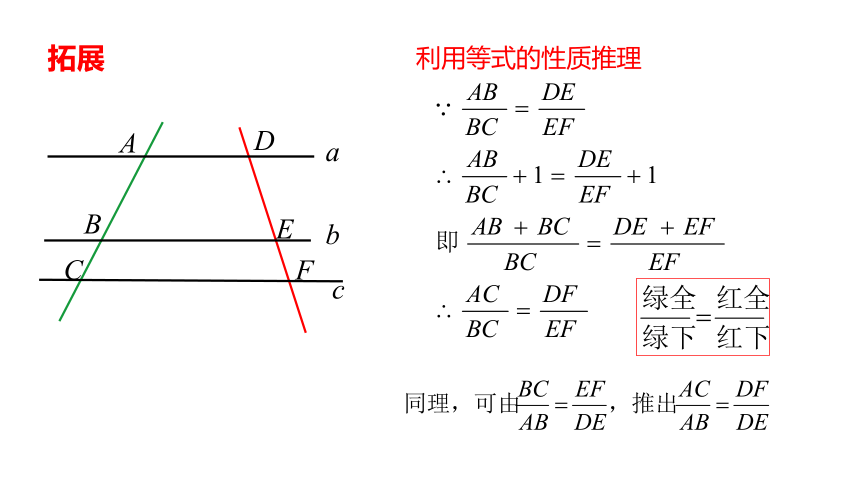
拓展
利用等式的性质推理
a
b
c
A
B
C
D
E
F
拓展
a
b
c
A
B
C
D
E
F
根据比例的基本性质
你发现了什么?
a
b
c
A
B
C
D
E
F
两条直线被一组平行线所截的线段对应成比例,在所有比例式中,处于交叉相乘位置的一定是不同直线上的两条线段.
如图所示,直线l1//l2//l3时,你能得到对应线段成比例吗?
例1 如图,两条直线a,b被三条直线c,d,e所截,交点分别是A、D、F和B、C、E.判断下列等式是否正确.
a
b
c
A
B
C
D
E
F
e
d
×
例题讲解
×
√
×
√
例2 已知a//b//c,AB=3,BC=5,DF=12,求DE和EF的长.
a
b
c
A
B
C
D
E
F
注意:①哪些线段是被平行线所截的?
②如何选择合适的比例式,去求线段长?
AB、BC、DE、EF
分析:由于要用到已知条件,去计算所要求的线段长,因此需要把已知的线段和所求的线段放到一个比例式中.
解:∵a//b//c
a
b
c
A
B
C
D
E
F
1.如图所示,已知AB//CD//EF,那么下列结论中错误的是( )
A.
B.
C.
D.
C
随堂演练
2.如图所示,已知直线a//b//c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,DF=4.5,BD=3,则AE等于( )
A.7 B.7.5 C.8 D.10
D
3.如图所示,直线l1//l2//l3,另两条直线分别交l1,l2,l3于点A,B,C及D,E,F,且AB=3,DE=4,EF=2,则BC= .
4.如图所示,AD//BE//CF,直线l1,l2与直线AD,BE,CF分别交于点A,B,C和点D,E,F.已知AB=4,BC=5,DE=5,求DF的长.
解:∵AD//BE//CF,
∴EF= ,
∴DF=DE+EF=5+
5.如图,已知直线a//b//c,两条直线与这三条平行线分别交于点A、B、C和点D、E、F,
a
b
c
A
B
C
D
E
F
解:∵a//b//c
设AB=2k,BC=5k
则AC=2k+5k=7k
(要求步骤完整)
课堂小结
基本事实
两条直线被一组平行线所截,截得的对应线段成比例
第二十五章 图形的相似
25.2 第1课时 平行线分线段成比例
1.什么是线段的比
2.什么是成比例线段
3.你能不通过测量快速将一根绳子分成两部分,
使得这两部分的比是2 ∶ 3
知识回顾
复习
观察与思考
下图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
A1B1=B1C1,
情景导入
如图,两条直线AC,DF被三条平行线a,b,c所截,截得的四条线段分别为AB、BC、DE、EF,平行线a,b之间的距离为d1,b,之间的距离为d2
a
b
c
A
B
C
D
E
F
Q
P
N
M
作AM⊥b于点M,BN⊥c于点N.
易证△ABM≌△BCN.
获取新知
一起探究
d1
d1
d2
d2
a
b
c
A
B
C
D
E
F
G
H
M
N
P
Q
由探究(1)的结论可得,AG=GB=BH=HM=MC,
DN=NE=EP=PQ=QF
a
b
c
A
B
C
D
E
F
我们按照探究(2)的方法仍然可以得到:
一、基本事实:两条直线被一组平行线所截,截得的
对应线段成比例.
a
b
c
A
B
C
D
E
F
几何语言:
∵a//b//c
一般指三条平行线
①由比例的基本性质可得
总结:只要比例式能化为AB·EF=BC·DE即可。
即让AB与EF、BC与DE位于比例式中的交叉位置.
a
b
c
A
B
C
D
E
F
拓展
利用等式的性质推理
a
b
c
A
B
C
D
E
F
拓展
a
b
c
A
B
C
D
E
F
根据比例的基本性质
你发现了什么?
a
b
c
A
B
C
D
E
F
两条直线被一组平行线所截的线段对应成比例,在所有比例式中,处于交叉相乘位置的一定是不同直线上的两条线段.
如图所示,直线l1//l2//l3时,你能得到对应线段成比例吗?
例1 如图,两条直线a,b被三条直线c,d,e所截,交点分别是A、D、F和B、C、E.判断下列等式是否正确.
a
b
c
A
B
C
D
E
F
e
d
×
例题讲解
×
√
×
√
例2 已知a//b//c,AB=3,BC=5,DF=12,求DE和EF的长.
a
b
c
A
B
C
D
E
F
注意:①哪些线段是被平行线所截的?
②如何选择合适的比例式,去求线段长?
AB、BC、DE、EF
分析:由于要用到已知条件,去计算所要求的线段长,因此需要把已知的线段和所求的线段放到一个比例式中.
解:∵a//b//c
a
b
c
A
B
C
D
E
F
1.如图所示,已知AB//CD//EF,那么下列结论中错误的是( )
A.
B.
C.
D.
C
随堂演练
2.如图所示,已知直线a//b//c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,DF=4.5,BD=3,则AE等于( )
A.7 B.7.5 C.8 D.10
D
3.如图所示,直线l1//l2//l3,另两条直线分别交l1,l2,l3于点A,B,C及D,E,F,且AB=3,DE=4,EF=2,则BC= .
4.如图所示,AD//BE//CF,直线l1,l2与直线AD,BE,CF分别交于点A,B,C和点D,E,F.已知AB=4,BC=5,DE=5,求DF的长.
解:∵AD//BE//CF,
∴EF= ,
∴DF=DE+EF=5+
5.如图,已知直线a//b//c,两条直线与这三条平行线分别交于点A、B、C和点D、E、F,
a
b
c
A
B
C
D
E
F
解:∵a//b//c
设AB=2k,BC=5k
则AC=2k+5k=7k
(要求步骤完整)
课堂小结
基本事实
两条直线被一组平行线所截,截得的对应线段成比例
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
