冀教版数学九年级上册同步课件:25.4第2课时 相似三角形的判定定理2(共16张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:25.4第2课时 相似三角形的判定定理2(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:32:04 | ||
图片预览






文档简介
(共16张PPT)
第二十五章 图形的相似
25.4 第2课时 相似三角形的判定定理2
判断两个三角形相似,你有哪些方法?
方法1:通过定义(不常用)
方法2:通过平行线
方法3:两角对应相等
A型
8型
知识回顾
方法4:利用传递性
三个角对应相等
三条边对应成比例
问题1 有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
观察与思考
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
获取新知
①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?由此可推出∠C′=∠C吗?为什么?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?与你周围的同学交流.
我发现这两个三角形是相似的
画一画
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE//B′C′,交A′C′于点E.
∵DE//B′C′,
∴△A′DE∽△A′B′C′.
求证:△A′B′C′∽△ABC.
B
A
C
B'
A'
D
E
C'
验证猜想
∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
∴
3
3
C
C
60°
)
4
A
B
)
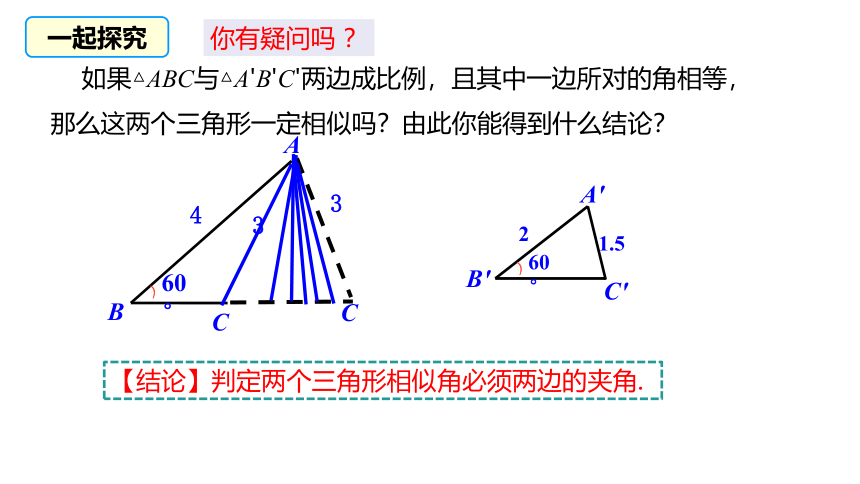
【结论】判定两个三角形相似角必须两边的夹角.
C′
1.5
B′
2
60°
A′
如果△ABC与△A'B'C'两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
一起探究
你有疑问吗 ?
判定定理二:两边对应成比例且夹角相等的两三角形相似.
A
B
C
D
E
F
几何语言:
∵ ∠A=∠D.
∴△ABC∽△DEF
例1 已知:在△ABC与△A′B′C′中,∠A=∠A′=60°, AB=4 cm,AC=8 cm,A′B′=11 cm,A′C′=22 cm. 求证:△ABC∽△A′B′C′.
例题讲解
证明:∵
∴
又∵ ∠A=∠A′=60°,
∴△ABC∽△A′B′C′.
解:∵ AE=1.5,AC=2
例2 如图,D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
∴
又∵∠EAD=∠CAB
∴ △ADE ∽△ABC
∴
∴
提示:解题时要找准对应边.
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB,
∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
例3 如图,在△ABC中,CD是边AB上的高,且 ,
求证 :∠ACB=90°.
A
B
C
D
∵
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
1. 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是 ( )
A. AC : BC=AD : BD
B. AC : BC=AB : AD
C. AB2 = CD · BC
D. AB2 = BD · BC
D
A
B
C
D
随堂演练
2.如图,已知△ABC,则下列四个三角形中,与△ABC相似的是( )
C
3.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.OA∶OC=OB∶OD,则下列结论中一定正确的是( )
A.①和②相似
B. ①和③相似
C. ①和④相似
D.②和④相似
B
解析:当 △ADP ∽△ACB 时,
AP : AB =AD : AC ,∴ AP : 12 =6 : 8 ,
解得 AP = 9;
当 △ADP ∽△ABC 时,
AD : AB =AP : AC ,∴ 6 : 12 = AP : 8 ,
解得 AP = 4.
∴ 当 AP 的长度为 4 或 9 时,
△ADP 和 △ABC 相似.
4. 如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC= 8,AD= 6,当AP的长度为 时,△ADP 和△ABC相似.
A
B
C
D
4或9
P
P
5. 如图,在四边形ABCD中,已知 ∠B =∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
A
B
C
D
解:∵AB=6,BC=4,AC=5,CD= ,
∴
又∵∠B=∠ACD,
∴ △ABC ∽ △DCA,
∴ ,
∴
课堂小结
利用两边及夹角判定三角形相似
两边对应成比例且夹角相等的两个三角形相似.
第二十五章 图形的相似
25.4 第2课时 相似三角形的判定定理2
判断两个三角形相似,你有哪些方法?
方法1:通过定义(不常用)
方法2:通过平行线
方法3:两角对应相等
A型
8型
知识回顾
方法4:利用传递性
三个角对应相等
三条边对应成比例
问题1 有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
观察与思考
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
获取新知
①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?由此可推出∠C′=∠C吗?为什么?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?与你周围的同学交流.
我发现这两个三角形是相似的
画一画
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE//B′C′,交A′C′于点E.
∵DE//B′C′,
∴△A′DE∽△A′B′C′.
求证:△A′B′C′∽△ABC.
B
A
C
B'
A'
D
E
C'
验证猜想
∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
∴
3
3
C
C
60°
)
4
A
B
)
【结论】判定两个三角形相似角必须两边的夹角.
C′
1.5
B′
2
60°
A′
如果△ABC与△A'B'C'两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
一起探究
你有疑问吗 ?
判定定理二:两边对应成比例且夹角相等的两三角形相似.
A
B
C
D
E
F
几何语言:
∵ ∠A=∠D.
∴△ABC∽△DEF
例1 已知:在△ABC与△A′B′C′中,∠A=∠A′=60°, AB=4 cm,AC=8 cm,A′B′=11 cm,A′C′=22 cm. 求证:△ABC∽△A′B′C′.
例题讲解
证明:∵
∴
又∵ ∠A=∠A′=60°,
∴△ABC∽△A′B′C′.
解:∵ AE=1.5,AC=2
例2 如图,D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
∴
又∵∠EAD=∠CAB
∴ △ADE ∽△ABC
∴
∴
提示:解题时要找准对应边.
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB,
∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
例3 如图,在△ABC中,CD是边AB上的高,且 ,
求证 :∠ACB=90°.
A
B
C
D
∵
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
1. 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是 ( )
A. AC : BC=AD : BD
B. AC : BC=AB : AD
C. AB2 = CD · BC
D. AB2 = BD · BC
D
A
B
C
D
随堂演练
2.如图,已知△ABC,则下列四个三角形中,与△ABC相似的是( )
C
3.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.OA∶OC=OB∶OD,则下列结论中一定正确的是( )
A.①和②相似
B. ①和③相似
C. ①和④相似
D.②和④相似
B
解析:当 △ADP ∽△ACB 时,
AP : AB =AD : AC ,∴ AP : 12 =6 : 8 ,
解得 AP = 9;
当 △ADP ∽△ABC 时,
AD : AB =AP : AC ,∴ 6 : 12 = AP : 8 ,
解得 AP = 4.
∴ 当 AP 的长度为 4 或 9 时,
△ADP 和 △ABC 相似.
4. 如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC= 8,AD= 6,当AP的长度为 时,△ADP 和△ABC相似.
A
B
C
D
4或9
P
P
5. 如图,在四边形ABCD中,已知 ∠B =∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
A
B
C
D
解:∵AB=6,BC=4,AC=5,CD= ,
∴
又∵∠B=∠ACD,
∴ △ABC ∽ △DCA,
∴ ,
∴
课堂小结
利用两边及夹角判定三角形相似
两边对应成比例且夹角相等的两个三角形相似.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
