冀教版数学九年级上册同步课件:25.5 第1课时 相似三角形的性质1(共18张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:25.5 第1课时 相似三角形的性质1(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 236.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:33:28 | ||
图片预览


文档简介
(共18张PPT)
第二十五章 图形的相似
25.5 第1课时 相似三角形的性质1
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例;
④直角三角形中,斜边和直角边对应成比例
知识回顾
A
B
C
A'
B'
C'
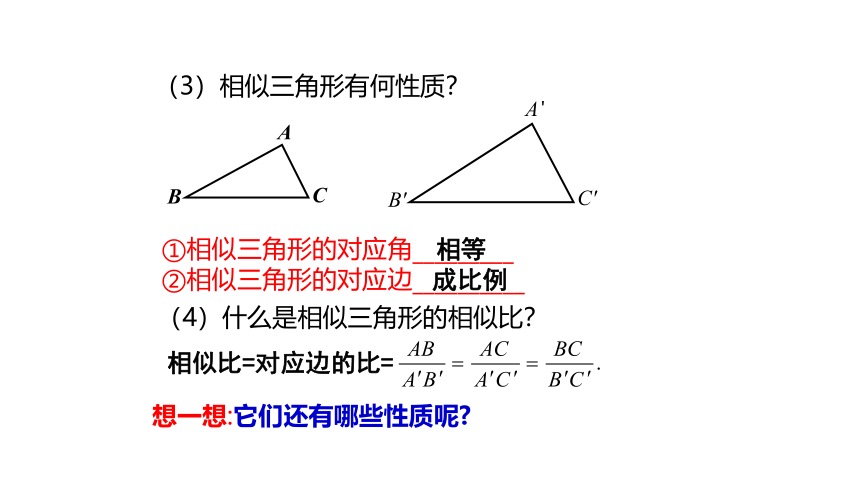
①相似三角形的对应角_________
②相似三角形的对应边__________
想一想:它们还有哪些性质呢
(3)相似三角形有何性质?
(4)什么是相似三角形的相似比?
相似比=对应边的比=
相等
成比例
D'
C'
B'
A'
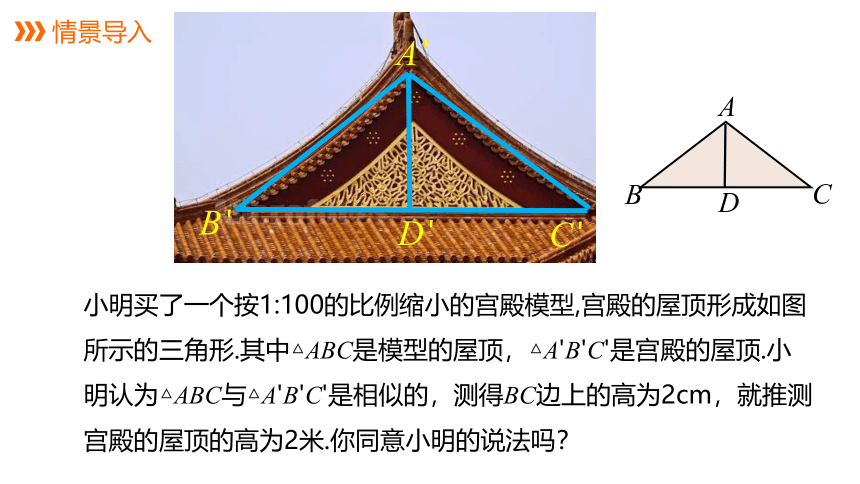
小明买了一个按1:100的比例缩小的宫殿模型,宫殿的屋顶形成如图所示的三角形.其中△ABC是模型的屋顶,△A'B'C'是宫殿的屋顶.小明认为△ABC与△A'B'C'是相似的,测得BC边上的高为2cm,就推测宫殿的屋顶的高为2米.你同意小明的说法吗?
A
D
C
B
情景导入
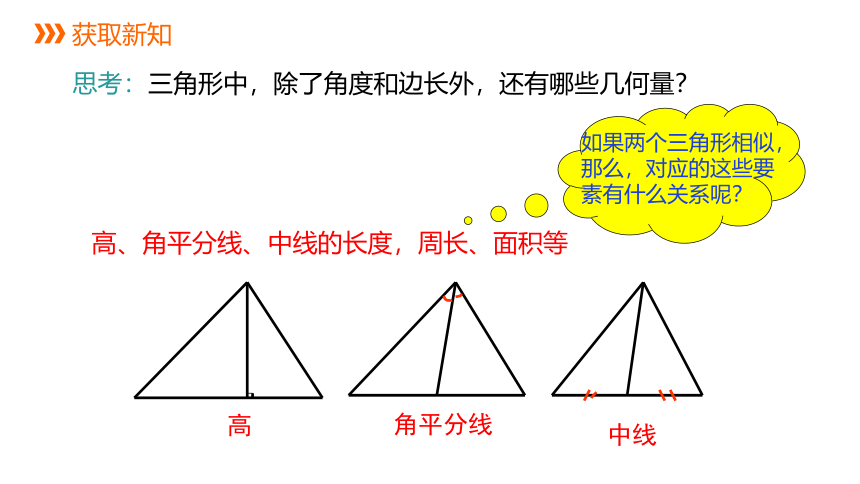
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
获取新知
如果两个三角形相似,
那么,对应的这些要素有什么关系呢?
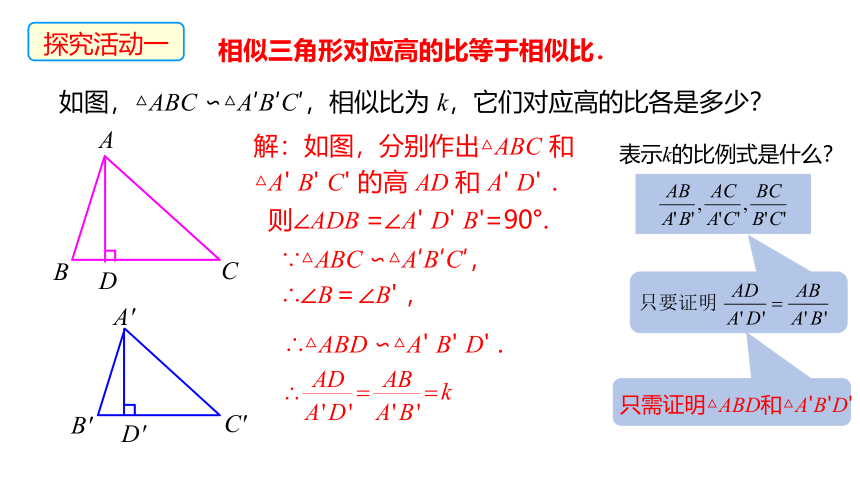
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高的比各是多少?
A
B
C
A'
B'
C'
探究活动一
D
D'
解:如图,分别作出△ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
∴△ABD ∽△A' B' D' .
表示k的比例式是什么?
只需证明△ABD和△A'B'D'
相似三角形对应高的比等于相似比.
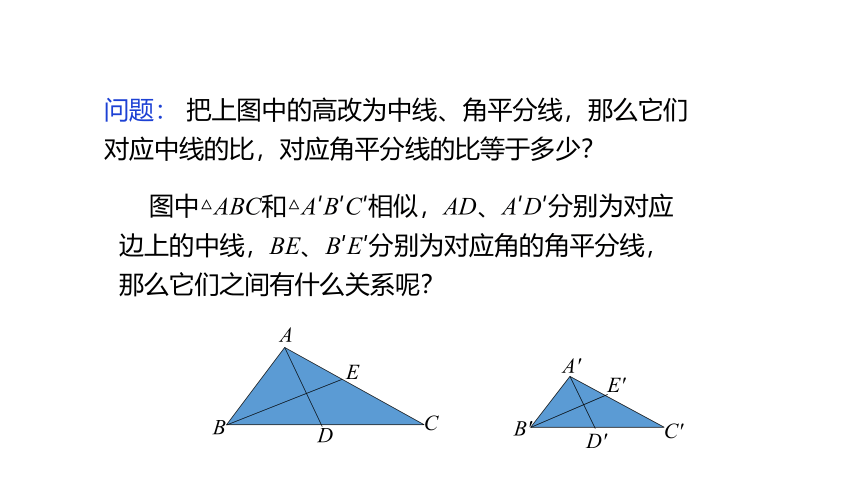
问题: 把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
已知:△ABC∽△A′B′C′,相似比为k, AD、A′D'分别是边BC和B'C'上的中线.求证:
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想1
证明:∵△ABC∽△A'B'C'
∴∠B=∠B',
∵AD、A'D'分别为△ABC和△A'B'C'的中线
∴△ABD∽△A'B'D'
结论:相似三角形的对应中线的比等于相似比
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想2
已知:△ABC∽△A′B′C′,相似比为k, AE、A′E'分别是边∠ABC和∠A′B'C'的角平分线.
求证:
证明:∵△ABC∽△A'B'C',
∴∠BAC=∠B'A'C' .
又∵AE、A′E'分别是边∠ABC和∠A′B'C'的角平分线,
结论:相似三角形的对应角平分线的比等于相似比
∴ △ABE∽△A′B′E′.
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
归纳总结
相似三角形性质定理:
∵△ABC∽△A′B′C′
∴
A
B
C
D
E
A'
B'
C'
D'
E'
F
F'
一般地,我们有:
相似三角形对应线段的比等于相似比.
例1 如图,在△ABC中,AD⊥BC,垂足为D,EF//BC,分别交AB,AC,AD于点E,F,G, , AD=15.求AG的长.
①
②
③
④
①
三角形的高出现
②
相似三角形
③
相似比
④
A
B
C
E
F
D
G
△ABC的高
所求AG
△AEF的高
解题思路:相似三角形对应高的比等于相似比.
例题讲解
A
B
C
E
F
D
G
解:∵EF∥BC
∴△AEF∽△ABC
∴AD⊥BC
∴AG⊥EF
解得,AG=9
(相似三角形对应高的比等于相似比)
例1.(拓展)如图,一块材料的形状是锐角△ABC,边BC=12cm,高AD=8cm,把它加工成正方形零件PQMN,要使正方形的一边在BC上,其余两个顶点分别在AB,AC上.求这个正方形零件的边长.
A
B
C
N
M
Q
P
D
分析:
1.从图形中提取与例1相同的图形
2.思路:相似三角形对应高的比等于相似比.
解:设PQ与AD交于点E
∵四边形PQMN是正方形
∴PQ//BC
∴△APQ∽△ABC
设正方形的边长为x,则PQ=x,AE=8-x
解得,x=4.8
∴这个正方形零件的边长是4.8cm.
(相似三角形对应高的比等于相似比)
E
ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=3cm ,则 ΔABC与ΔA1B1C1的对应高之比为 .
8:3
随堂演练
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
(相似三角形对应角平
线的比等于相似比),
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
5.如图,在△ABC中,点D,E分别在边AC,AB上,AG⊥BC于G,AF⊥DE于点F,∠EAF=∠GAC,若AD=3,AB=5,求AF:AG.
A
B
C
D
E
F
G
解:∵∠EAF=∠GAC,∠AFE=∠AGC=90°
∴△AFE∽△AGC
∴∠AED=∠C
又∵∠EAD=∠CAB
∴△AED∽△ACB
(相似三角形对应高的比等于相似比)
课堂小结
相似三角形的性质
3.对应线段(高、中线、角平分线)的比等于相似比
1.对应角相等
2.对应边成比例
相等的角、求角的度数
证比例式(等积式)
求线段长
第二十五章 图形的相似
25.5 第1课时 相似三角形的性质1
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例;
④直角三角形中,斜边和直角边对应成比例
知识回顾
A
B
C
A'
B'
C'
①相似三角形的对应角_________
②相似三角形的对应边__________
想一想:它们还有哪些性质呢
(3)相似三角形有何性质?
(4)什么是相似三角形的相似比?
相似比=对应边的比=
相等
成比例
D'
C'
B'
A'
小明买了一个按1:100的比例缩小的宫殿模型,宫殿的屋顶形成如图所示的三角形.其中△ABC是模型的屋顶,△A'B'C'是宫殿的屋顶.小明认为△ABC与△A'B'C'是相似的,测得BC边上的高为2cm,就推测宫殿的屋顶的高为2米.你同意小明的说法吗?
A
D
C
B
情景导入
思考:三角形中,除了角度和边长外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
获取新知
如果两个三角形相似,
那么,对应的这些要素有什么关系呢?
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高的比各是多少?
A
B
C
A'
B'
C'
探究活动一
D
D'
解:如图,分别作出△ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
∴△ABD ∽△A' B' D' .
表示k的比例式是什么?
只需证明△ABD和△A'B'D'
相似三角形对应高的比等于相似比.
问题: 把上图中的高改为中线、角平分线,那么它们对应中线的比,对应角平分线的比等于多少?
图中△ABC和△A′B′C′相似,AD、A′D′分别为对应边上的中线,BE、B′E′分别为对应角的角平分线,那么它们之间有什么关系呢?
A
B
C
D
E
A'
B'
D'
C'
E'
已知:△ABC∽△A′B′C′,相似比为k, AD、A′D'分别是边BC和B'C'上的中线.求证:
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想1
证明:∵△ABC∽△A'B'C'
∴∠B=∠B',
∵AD、A'D'分别为△ABC和△A'B'C'的中线
∴△ABD∽△A'B'D'
结论:相似三角形的对应中线的比等于相似比
A'
B'
D'
C'
E'
A
B
C
D
E
验证猜想2
已知:△ABC∽△A′B′C′,相似比为k, AE、A′E'分别是边∠ABC和∠A′B'C'的角平分线.
求证:
证明:∵△ABC∽△A'B'C',
∴∠BAC=∠B'A'C' .
又∵AE、A′E'分别是边∠ABC和∠A′B'C'的角平分线,
结论:相似三角形的对应角平分线的比等于相似比
∴ △ABE∽△A′B′E′.
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
归纳总结
相似三角形性质定理:
∵△ABC∽△A′B′C′
∴
A
B
C
D
E
A'
B'
C'
D'
E'
F
F'
一般地,我们有:
相似三角形对应线段的比等于相似比.
例1 如图,在△ABC中,AD⊥BC,垂足为D,EF//BC,分别交AB,AC,AD于点E,F,G, , AD=15.求AG的长.
①
②
③
④
①
三角形的高出现
②
相似三角形
③
相似比
④
A
B
C
E
F
D
G
△ABC的高
所求AG
△AEF的高
解题思路:相似三角形对应高的比等于相似比.
例题讲解
A
B
C
E
F
D
G
解:∵EF∥BC
∴△AEF∽△ABC
∴AD⊥BC
∴AG⊥EF
解得,AG=9
(相似三角形对应高的比等于相似比)
例1.(拓展)如图,一块材料的形状是锐角△ABC,边BC=12cm,高AD=8cm,把它加工成正方形零件PQMN,要使正方形的一边在BC上,其余两个顶点分别在AB,AC上.求这个正方形零件的边长.
A
B
C
N
M
Q
P
D
分析:
1.从图形中提取与例1相同的图形
2.思路:相似三角形对应高的比等于相似比.
解:设PQ与AD交于点E
∵四边形PQMN是正方形
∴PQ//BC
∴△APQ∽△ABC
设正方形的边长为x,则PQ=x,AE=8-x
解得,x=4.8
∴这个正方形零件的边长是4.8cm.
(相似三角形对应高的比等于相似比)
E
ΔABC∽ ΔA1B1C1 ,BD和B1D1是它们的中线,
已知 ,B1D1 =4cm,则BD= cm.
6
2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分线,已知AD=8cm, A1D1=3cm ,则 ΔABC与ΔA1B1C1的对应高之比为 .
8:3
随堂演练
3.如图、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=2m,CD=4m,点P到CD的距离是3m,则P到AB的距离是 m.
P
A
D
B
C
2
4
1.5
解:∵ △ABC∽△DEF,
解得,EH=3.2(cm).
答:EH的长为3.2cm.
A
G
B
C
D
E
F
H
(相似三角形对应角平
线的比等于相似比),
4.已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
5.如图,在△ABC中,点D,E分别在边AC,AB上,AG⊥BC于G,AF⊥DE于点F,∠EAF=∠GAC,若AD=3,AB=5,求AF:AG.
A
B
C
D
E
F
G
解:∵∠EAF=∠GAC,∠AFE=∠AGC=90°
∴△AFE∽△AGC
∴∠AED=∠C
又∵∠EAD=∠CAB
∴△AED∽△ACB
(相似三角形对应高的比等于相似比)
课堂小结
相似三角形的性质
3.对应线段(高、中线、角平分线)的比等于相似比
1.对应角相等
2.对应边成比例
相等的角、求角的度数
证比例式(等积式)
求线段长
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
