冀教版数学九年级上册同步课件:25.5 第2课时 相似三角形的性质2(共19张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:25.5 第2课时 相似三角形的性质2(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 305.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 15:17:05 | ||
图片预览





文档简介
(共19张PPT)
第二十五章 图形的相似
25.5 第2课时 相似三角形的性质2
1、相似三角形的判定
两组角对应相等、三组边对应成比例、
两组边对应成比例且夹角相等
对应角______对应边______
对应高的比等于______
对应角平分线的比等于______
对应中线的比等于_____
相等
成比例
相似比
相似比
相似比
知识回顾
复习
2、相似三角形的性质
小明的妈妈过生日,小明提前预定了一个12寸的蛋糕.生日当天,小明去蛋糕店取蛋糕.(友情提示:12寸是蛋糕的直径哦)由于蛋糕店的失误,把订的12寸的蛋糕做成了6寸.蛋糕店给的赔偿建议为给两个厚度与12寸的蛋糕厚度一样的6寸的蛋糕,请问这样做,能拿到和原来一样大的蛋糕吗?谈谈你的看法.
情景导入
2个6寸的蛋糕面积=1个12寸蛋糕的面积吗?
当圆的半径扩大为2倍时,面积会扩大为4倍.那么当一个三角形的各边长扩大为原来的2倍时,面积会发生怎样的变化呢?
∴小明拿到的蛋糕比原来的小.
获取新知
一起探究
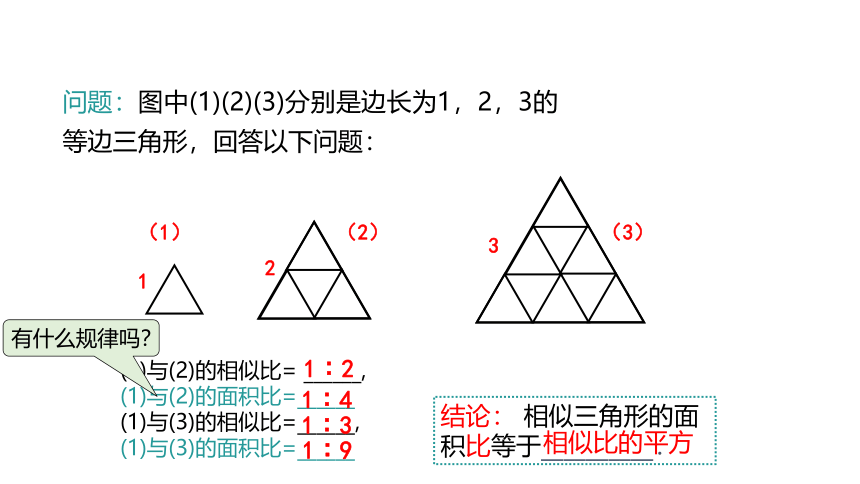
(1)与(2)的相似比= ______,
(1)与(2)的面积比=______
(1)与(3)的相似比=______,
(1)与(3)的面积比=______
1
2
3
1∶2
(1)
(2)
(3)
1∶4
1∶3
1∶9
问题:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,回答以下问题:
结论: 相似三角形的面积比等于__________.
相似比的平方
有什么规律吗?
证明:设△ABC∽△A′B′C′,相似比为k,
如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′.
A
B
C
A′
B′
C′
D
D′
想一想:怎么证明这一结论呢?
∵△ABC∽△A′B′C′.
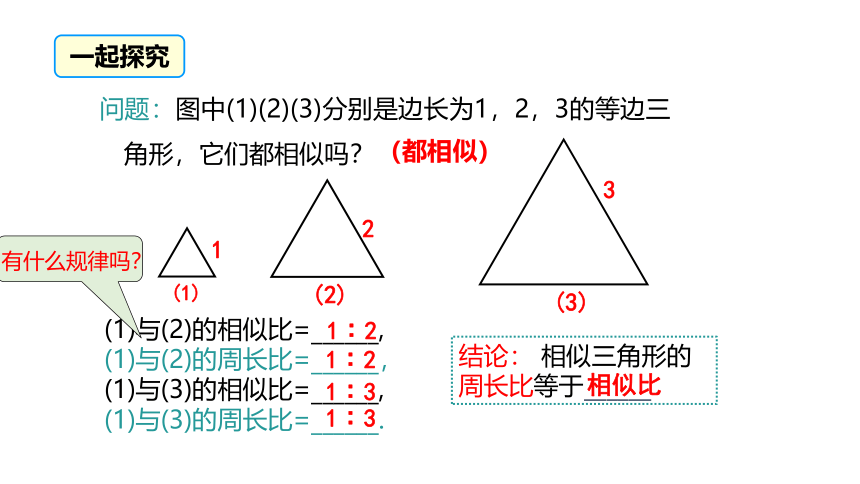
问题:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(3)的相似比=______,
(1)与(3)的周长比=______.
1∶2
结论: 相似三角形的周长比等于______.
相似比
(都相似)
1∶3
1∶2
1∶3
有什么规律吗?
一起探究
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
想一想:怎么证明这一结论呢?
相似三角形周长、面积的比
相似三角形面积的比等于相似比的平方.
相似三角形周长的比等于相似比.
例题讲解
例1 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点. 求:
(1)△DEF的周长与△ABC的周长之比.
(2)△DEF的面积与△ABC的面积之比.
解:∵D,E,F分别为BC,AC,AB的中点,
∴ DE∥AB, EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF的周长与△ABC的周长之比为1∶2,
△DEF的面积与△ABC的面积之比为1∶4.
解:在△ABC和△DEF中
∵ AB=2DE,AC=2DF
又 ∵∠D=∠A
∴ △DEF ∽ △ABC ,相似比为 1 : 2
A
B
C
D
E
F
∴
例2 如图,在△ABC和△DEF中,AB=2DE ,AC=2DF,∠A=∠D. 若△ABC的边BC上的高为6,面积为 ,求△DEF的边EF上的高和面积.
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
1.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍 B.3倍 C.81倍 D.18倍
B
随堂演练
2.两个相似三角形的最短边长分别为5cm和3cm,它们的周长之差为12 cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
D
3.如图,在平行四边形ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A.
B.
C.
D.
D
4.已知△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,CD=4 cm,C′D′=10 cm,AE是△ABC的一条高,AE=4.8 cm,求△A′B′C′中对应高A′E′的长.
解:∵△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,且AE,A′E′是对应的高线,
∴A′E′=12 cm.
即
5.已知△ABC∽△DEF,△ABC和△DEF的周长分别为20 cm和25 cm,且BC=5 cm,DF=4 cm,求EF和AC的长.
解:∵相似三角形周长的比等于相似比,
同理可得
6.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6 cm2,求S△CDF的值.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴△CDF∽△AEF.
∵AE∶EB=1∶2,
∴AE∶AB=1∶3,
∴AE∶CD=1∶3,
∴△AEF与△CDF的周长比为1∶3.
(2)∵△CDF∽△AEF,AE∶CD=1∶3,
∴S△AEF∶S△CDF=1∶9,
∴S△CDF=9S△AEF=54 cm2.
相似三角形的性质2
周长的比
相似三角形周长的比等于相似比.
面积的比
相似三角形面积的比等于相似比的平方.
课堂小结
第二十五章 图形的相似
25.5 第2课时 相似三角形的性质2
1、相似三角形的判定
两组角对应相等、三组边对应成比例、
两组边对应成比例且夹角相等
对应角______对应边______
对应高的比等于______
对应角平分线的比等于______
对应中线的比等于_____
相等
成比例
相似比
相似比
相似比
知识回顾
复习
2、相似三角形的性质
小明的妈妈过生日,小明提前预定了一个12寸的蛋糕.生日当天,小明去蛋糕店取蛋糕.(友情提示:12寸是蛋糕的直径哦)由于蛋糕店的失误,把订的12寸的蛋糕做成了6寸.蛋糕店给的赔偿建议为给两个厚度与12寸的蛋糕厚度一样的6寸的蛋糕,请问这样做,能拿到和原来一样大的蛋糕吗?谈谈你的看法.
情景导入
2个6寸的蛋糕面积=1个12寸蛋糕的面积吗?
当圆的半径扩大为2倍时,面积会扩大为4倍.那么当一个三角形的各边长扩大为原来的2倍时,面积会发生怎样的变化呢?
∴小明拿到的蛋糕比原来的小.
获取新知
一起探究
(1)与(2)的相似比= ______,
(1)与(2)的面积比=______
(1)与(3)的相似比=______,
(1)与(3)的面积比=______
1
2
3
1∶2
(1)
(2)
(3)
1∶4
1∶3
1∶9
问题:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,回答以下问题:
结论: 相似三角形的面积比等于__________.
相似比的平方
有什么规律吗?
证明:设△ABC∽△A′B′C′,相似比为k,
如图,分别作出△ABC和△A′B′C′的高AD和A′D′.
∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,
∴△ABD∽△A′B′D′.
A
B
C
A′
B′
C′
D
D′
想一想:怎么证明这一结论呢?
∵△ABC∽△A′B′C′.
问题:图中(1)(2)(3)分别是边长为1,2,3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(3)的相似比=______,
(1)与(3)的周长比=______.
1∶2
结论: 相似三角形的周长比等于______.
相似比
(都相似)
1∶3
1∶2
1∶3
有什么规律吗?
一起探究
证明:设△ABC∽△A1B1C1,相似比为k,
求证:相似三角形的周长比等于相似比.
A
B
C
A1
B1
C1
想一想:怎么证明这一结论呢?
相似三角形周长、面积的比
相似三角形面积的比等于相似比的平方.
相似三角形周长的比等于相似比.
例题讲解
例1 如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点. 求:
(1)△DEF的周长与△ABC的周长之比.
(2)△DEF的面积与△ABC的面积之比.
解:∵D,E,F分别为BC,AC,AB的中点,
∴ DE∥AB, EF∥BC,DF∥AC,
∴△DEF∽△ABC.
∴△DEF的周长与△ABC的周长之比为1∶2,
△DEF的面积与△ABC的面积之比为1∶4.
解:在△ABC和△DEF中
∵ AB=2DE,AC=2DF
又 ∵∠D=∠A
∴ △DEF ∽ △ABC ,相似比为 1 : 2
A
B
C
D
E
F
∴
例2 如图,在△ABC和△DEF中,AB=2DE ,AC=2DF,∠A=∠D. 若△ABC的边BC上的高为6,面积为 ,求△DEF的边EF上的高和面积.
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
1.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍 B.3倍 C.81倍 D.18倍
B
随堂演练
2.两个相似三角形的最短边长分别为5cm和3cm,它们的周长之差为12 cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
D
3.如图,在平行四边形ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A.
B.
C.
D.
D
4.已知△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,CD=4 cm,C′D′=10 cm,AE是△ABC的一条高,AE=4.8 cm,求△A′B′C′中对应高A′E′的长.
解:∵△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,且AE,A′E′是对应的高线,
∴A′E′=12 cm.
即
5.已知△ABC∽△DEF,△ABC和△DEF的周长分别为20 cm和25 cm,且BC=5 cm,DF=4 cm,求EF和AC的长.
解:∵相似三角形周长的比等于相似比,
同理可得
6.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6 cm2,求S△CDF的值.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,
∴△CDF∽△AEF.
∵AE∶EB=1∶2,
∴AE∶AB=1∶3,
∴AE∶CD=1∶3,
∴△AEF与△CDF的周长比为1∶3.
(2)∵△CDF∽△AEF,AE∶CD=1∶3,
∴S△AEF∶S△CDF=1∶9,
∴S△CDF=9S△AEF=54 cm2.
相似三角形的性质2
周长的比
相似三角形周长的比等于相似比.
面积的比
相似三角形面积的比等于相似比的平方.
课堂小结
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
