冀教版数学九年级上册同步课件:26.1 第1课时 正切(共23张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:26.1 第1课时 正切(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 396.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:36:15 | ||
图片预览






文档简介
(共23张PPT)
第二十六章 锐角三角函数
26.1 第1课时 正切
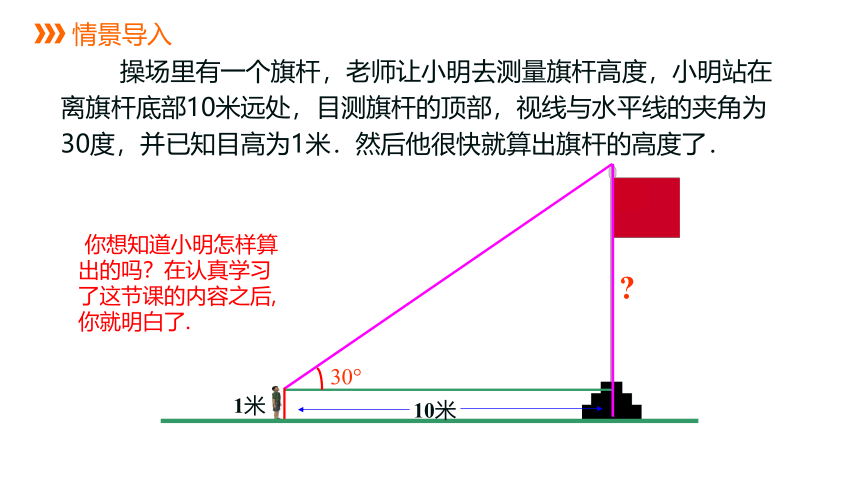
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1米.然后他很快就算出旗杆的高度了.
1米
10米
你想知道小明怎样算出的吗?在认真学习了这节课的内容之后,你就明白了.
情景导入
在直角三角形中,三边之间具有特殊关系(勾股定理), 两个锐角互余, 那么直角三角形的边和角之间是否也有着特殊的关系呢
做一做
轮船在A处时,灯塔B位于它的北偏东35°的方向上,轮船向东航行5km到达C处,灯塔在轮船的正北方(图26-1),此时轮船距灯塔多少千米
A
B
C
35°
北
东
图26-1
获取新知
一起探究
A
B
C
α
A'
B'
C'
α
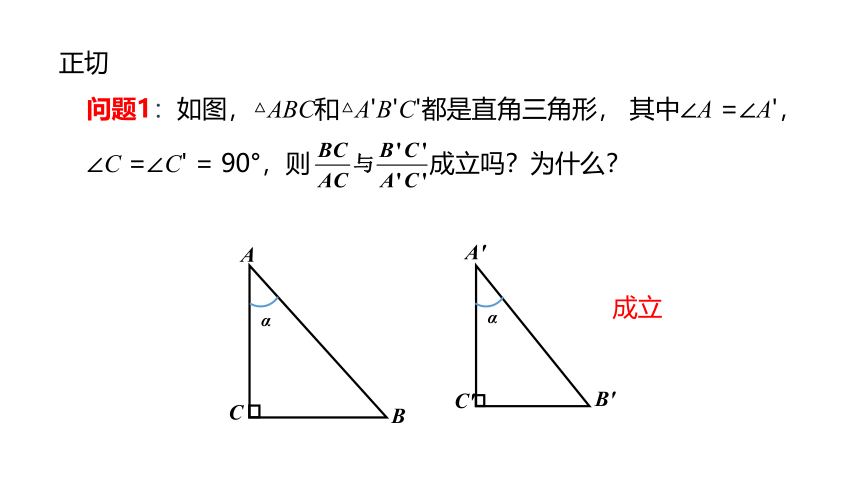
成立
正切
问题1:如图,△ABC和△A'B'C'都是直角三角形, 其中∠A =∠A',∠C =∠C' = 90°,则 成立吗?为什么?
A
B
C
α
A'
B'
C'
α
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
A'C'
AC
B'C'
BC
=
即
AC
BC
A'C'
B'C'
=
问题2:观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =_____ =_____.
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边和邻边的比值是唯一确定的.
我们每个人画出的三角形都和图中的 ABC相似,但对应边的长却可能不相等,那我们得到的比值相等吗?为什么?
我们把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
应该注意的几个问题:
1.tanA是在直角三角形中定义的,∠A必须是一个锐角。
2.tanA是一个完整的符号。在表示∠A的正切时,习惯省去“∠”号,但表示∠ ABC或∠1的正切,不能省略“∠” 号,应表示成tan ∠ ABC或tan ∠1。
3.tanA是一个比值无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边的长短无关.
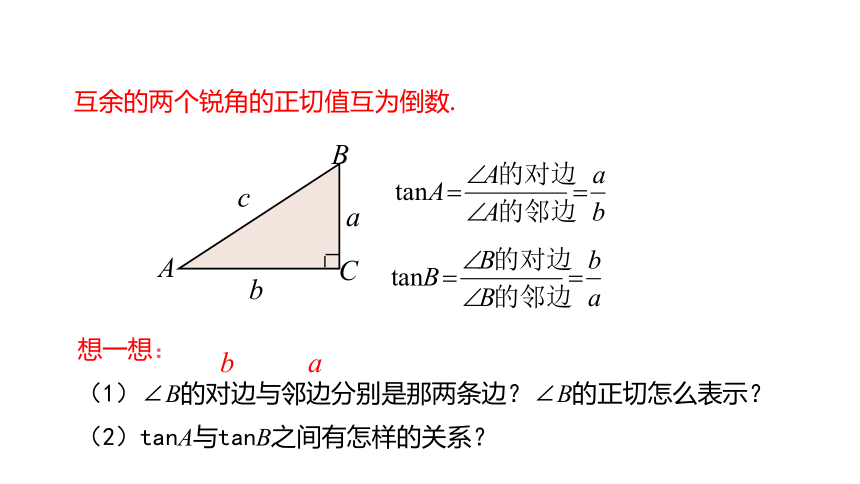
互余的两个锐角的正切值互为倒数.
A
C
B
a
b
c
想一想:
(1)∠B的对边与邻边分别是那两条边?∠B的正切怎么表示?
(2)tanA与tanB之间有怎样的关系?
b
a
例1 在Rt△ABC中,∠C=90°.
(1)如图(1)所示,∠A=30°,求tan A,tan B的值.
(2)如图(2)所示,∠A=45°,求tan A的值.
解:(1)在Rt△ABC中,
∵∠A=30°,
∴∠B=60°,且 .
∴ = = .
∴tan A=tan 30°= ,
tan B=tan 60°= .
特殊角的正切值
(2)在Rt△ABC中,
∵∠A=45°,
∴a=b.
∴tan A=tan 45°= .
30° 45° 60°
tan A
锐角三角函数
锐角A
1
正切是一个比值
例2 求一个角的正切值.
A
C
B
D
(1)如图,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD= ,则tan∠CAD的值是____.
2
方法①:求出角的对边和邻边的长度,直接用定义做.
例题讲解
(2)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,则tan∠BCD的值是____.
D
C
B
A
8
6
分析:直接去求∠BCD的对边与邻边的长计算量是比较大的.
这个图形是相似三角形中学过的“母子型”,有相等的角出现,
因此可把求∠BCD的正切转化为与求它相等的∠A的正切值.
方法②:转化为求与其相等的角的正切.
(3)如图,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值是____.
C
B
A
方法③求一个角的正切值应把这个角放到直角三角形中
例3 如图,在等腰△ABC中,∠C=90°,AC=6,点D是AC上一点,若tan∠DBC= ,求AD的长.
D
C
B
A
解:由题意得,BC=AC=6
在Rt△BCD中,
利用正切求边长
典例精析
例3 如图,在等腰△ABC中,∠C=90°,AC=6,点D是AC上一点,若tan∠DBC= ,求AD的长.
D
C
B
A
解:由题意得,BC=AC=6
在Rt△BCD中,
利用正切求边长
1.在Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值是____.
2.在Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC=____.
2
随堂演练
3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
A
B
C
┌
C
4.tan60°的值是____ ;若tanA=1,则∠A=_____.
45°
6.如果方程 的两个根分别是Rt△ABC的两条边,△ABC的最小角为∠A,那么tanA的值是_______.
分析:解方程得,x=1或x=3.
情况一:1,3均为直角边.
情况二:3为斜边.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BC=2,AB=3,求tan∠BCD的值.
解:∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°.
∵∠BCD+∠ACD=∠ACB=90°,
∴∠BCD=∠A.
在Rt△ABC中,
∴tanA= = ,
AC
BC
∴tan∠BCD=tanA= .
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BC=2,AB=3,求tan∠BCD的值.
解:∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°.
∵∠BCD+∠ACD=∠ACB=90°,
∴∠BCD=∠A.
在Rt△ABC中,
B
A
C
c
a
b
对边
邻边
课堂小结
正切
概念
特殊角的正切值
第二十六章 锐角三角函数
26.1 第1课时 正切
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1米.然后他很快就算出旗杆的高度了.
1米
10米
你想知道小明怎样算出的吗?在认真学习了这节课的内容之后,你就明白了.
情景导入
在直角三角形中,三边之间具有特殊关系(勾股定理), 两个锐角互余, 那么直角三角形的边和角之间是否也有着特殊的关系呢
做一做
轮船在A处时,灯塔B位于它的北偏东35°的方向上,轮船向东航行5km到达C处,灯塔在轮船的正北方(图26-1),此时轮船距灯塔多少千米
A
B
C
35°
北
东
图26-1
获取新知
一起探究
A
B
C
α
A'
B'
C'
α
成立
正切
问题1:如图,△ABC和△A'B'C'都是直角三角形, 其中∠A =∠A',∠C =∠C' = 90°,则 成立吗?为什么?
A
B
C
α
A'
B'
C'
α
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
A'C'
AC
B'C'
BC
=
即
AC
BC
A'C'
B'C'
=
问题2:观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =_____ =_____.
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边和邻边的比值是唯一确定的.
我们每个人画出的三角形都和图中的 ABC相似,但对应边的长却可能不相等,那我们得到的比值相等吗?为什么?
我们把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
应该注意的几个问题:
1.tanA是在直角三角形中定义的,∠A必须是一个锐角。
2.tanA是一个完整的符号。在表示∠A的正切时,习惯省去“∠”号,但表示∠ ABC或∠1的正切,不能省略“∠” 号,应表示成tan ∠ ABC或tan ∠1。
3.tanA是一个比值无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边的长短无关.
互余的两个锐角的正切值互为倒数.
A
C
B
a
b
c
想一想:
(1)∠B的对边与邻边分别是那两条边?∠B的正切怎么表示?
(2)tanA与tanB之间有怎样的关系?
b
a
例1 在Rt△ABC中,∠C=90°.
(1)如图(1)所示,∠A=30°,求tan A,tan B的值.
(2)如图(2)所示,∠A=45°,求tan A的值.
解:(1)在Rt△ABC中,
∵∠A=30°,
∴∠B=60°,且 .
∴ = = .
∴tan A=tan 30°= ,
tan B=tan 60°= .
特殊角的正切值
(2)在Rt△ABC中,
∵∠A=45°,
∴a=b.
∴tan A=tan 45°= .
30° 45° 60°
tan A
锐角三角函数
锐角A
1
正切是一个比值
例2 求一个角的正切值.
A
C
B
D
(1)如图,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD= ,则tan∠CAD的值是____.
2
方法①:求出角的对边和邻边的长度,直接用定义做.
例题讲解
(2)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,则tan∠BCD的值是____.
D
C
B
A
8
6
分析:直接去求∠BCD的对边与邻边的长计算量是比较大的.
这个图形是相似三角形中学过的“母子型”,有相等的角出现,
因此可把求∠BCD的正切转化为与求它相等的∠A的正切值.
方法②:转化为求与其相等的角的正切.
(3)如图,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值是____.
C
B
A
方法③求一个角的正切值应把这个角放到直角三角形中
例3 如图,在等腰△ABC中,∠C=90°,AC=6,点D是AC上一点,若tan∠DBC= ,求AD的长.
D
C
B
A
解:由题意得,BC=AC=6
在Rt△BCD中,
利用正切求边长
典例精析
例3 如图,在等腰△ABC中,∠C=90°,AC=6,点D是AC上一点,若tan∠DBC= ,求AD的长.
D
C
B
A
解:由题意得,BC=AC=6
在Rt△BCD中,
利用正切求边长
1.在Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值是____.
2.在Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC=____.
2
随堂演练
3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
A
B
C
┌
C
4.tan60°的值是____ ;若tanA=1,则∠A=_____.
45°
6.如果方程 的两个根分别是Rt△ABC的两条边,△ABC的最小角为∠A,那么tanA的值是_______.
分析:解方程得,x=1或x=3.
情况一:1,3均为直角边.
情况二:3为斜边.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BC=2,AB=3,求tan∠BCD的值.
解:∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°.
∵∠BCD+∠ACD=∠ACB=90°,
∴∠BCD=∠A.
在Rt△ABC中,
∴tanA= = ,
AC
BC
∴tan∠BCD=tanA= .
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BC=2,AB=3,求tan∠BCD的值.
解:∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°.
∵∠BCD+∠ACD=∠ACB=90°,
∴∠BCD=∠A.
在Rt△ABC中,
B
A
C
c
a
b
对边
邻边
课堂小结
正切
概念
特殊角的正切值
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
