冀教版数学九年级上册同步课件:26.3解直角三角形(共25张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:26.3解直角三角形(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第二十六章 解直角三角形
26.3 解直角三角形
A
C
B
c
b
a
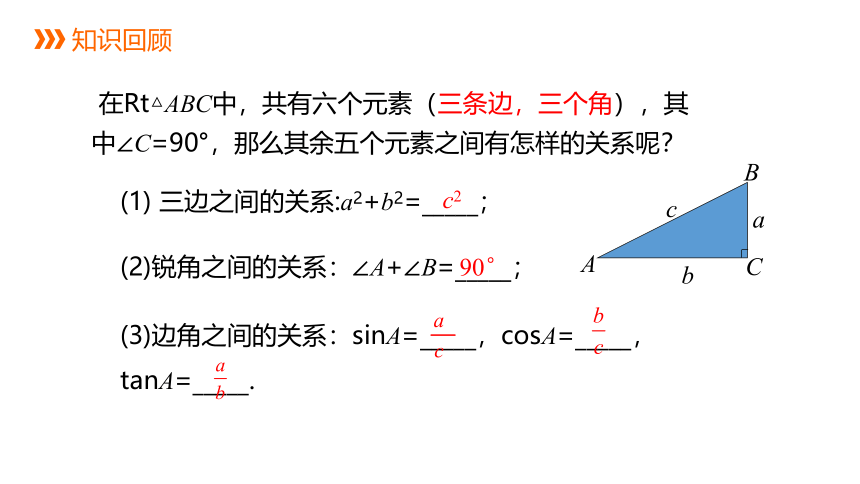
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
知识回顾
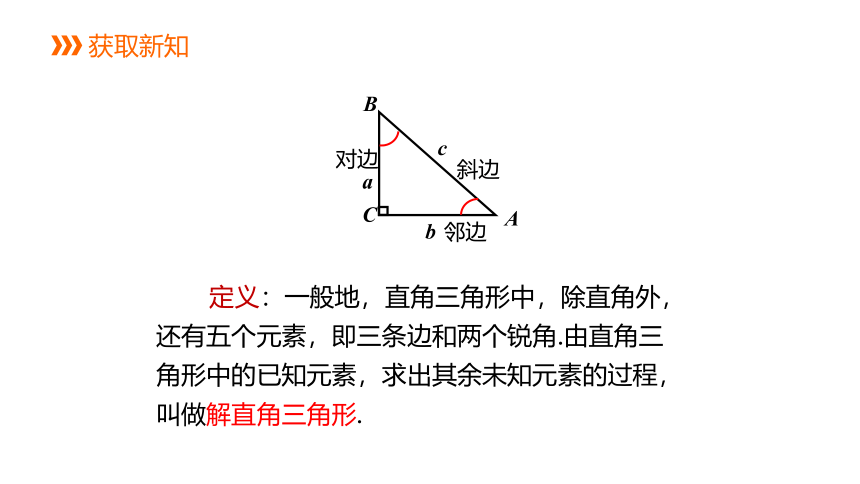
定义:一般地,直角三角形中,除直角外,还有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
B
A
C
c
a
b
对边
邻边
斜边
获取新知
直角三角形中,未知的5个元素之间的关系
①三边之间的关系
B
C
A
c
b
a
已知任意两边可求出第三边
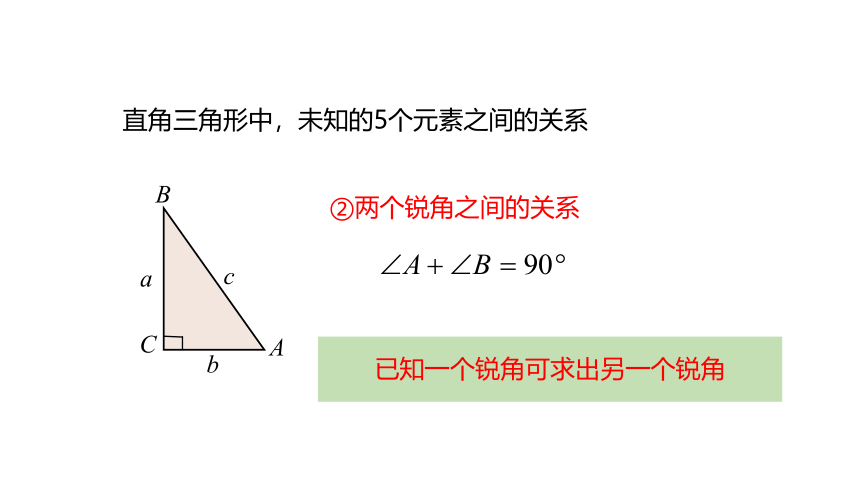
直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
已知一个锐角可求出另一个锐角
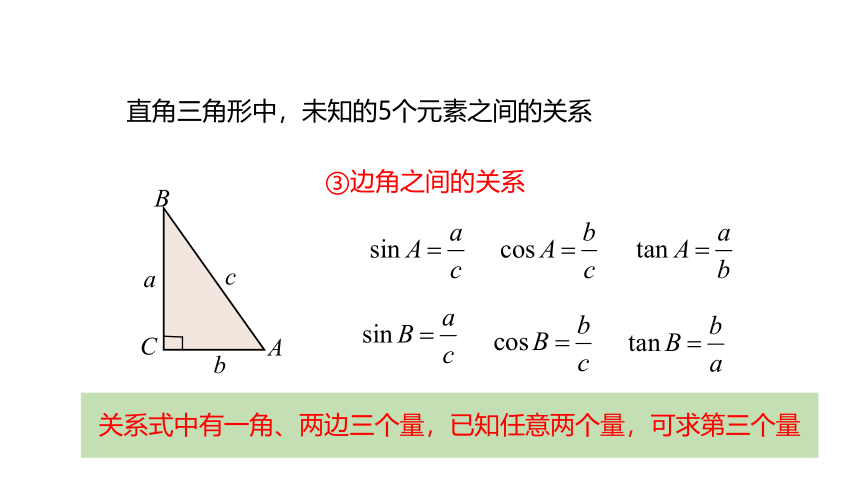
直角三角形中,未知的5个元素之间的关系
③边角之间的关系
B
C
A
c
b
a
关系式中有一角、两边三个量,已知任意两个量,可求第三个量
直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
根据以上关系,若知道五个元素中的两个元素(至少有一个是边),就可以求出其他三个元素.
①三边之间的关系
③边角之间的关系:
例1 如图,在Rt△ABC中,∠C=90°,∠A=34°,AC=6.解这个直角三角形.(结果精确到0.01)(sin34°≈0.60,cos34°≈0.56,tan34°≈0.67)
A
C
B
34°
6
尝试独立解决,再一起交流
(1)欲求的未知元素有哪些?
∠B、BC、AB
(2)如何求∠B
利用∠A+∠B=90°
例题讲解
A
C
B
34°
6
(3)如何求BC?
所求的BC与已知的AC的比构成tanA,用tanA=BC:AC来求.
(4)如何求AB
所求的AB与已知的AC的比构成cosA,用cosA=AC:AB来求.
把所求的线段和已知的线段放到一个比例式中,确定是哪个角的哪个三角函数
sin34°≈0.60,
cos34°≈0.83,
tan34°≈0.67
A
C
B
34°
6
解:∠B=90°-∠A=90°-34°=56°.
在Rt△ABC中
∴BC=AC·tanA=6×tan34°≈6×0.6745=4.047
想一想:求AB时,用勾股定理好不好?
指明是哪个直角三角形
指明是哪个三角函数
导公式、计算
不好,会增大结果的误差,应尽可能用原题中的数据.
例2 如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到1”)
A
C
B
8
15
(1)欲求的未知元素有哪些?
∠A、∠B、AB
(2)如何求∠A
已知的BC和AC的比构成tanA,用tanA=BC:AC来求.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
A
C
B
8
15
(3)如何求∠B
(4)如何求AB
利用勾股定理.
利用∠A+∠B=90°.
例2 如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到1”)
A
C
B
8
解:在Rt△ABC中
∴∠A=28°
想一想:求AB时,用sinA好不好?
由边长可导出角度
不好,会增大结果的误差,应尽可能用原题中的数据.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
15
∴∠B=90°-∠A=90°-28°=62°.
在Rt△ABC中,由勾股定理得
1、数形结合有利于分析问题;
2、选择关系式时,尽量使用原始数据,以防“累积误差”和“一错再错”;
3、解直角三角形时,应求出所有未知元素。
注意事项:
解直角三角形的原则:
(1)有角先求角,无角先求边
(2)有斜用弦, 无斜用切;
宁乘毋除, 取原避中。
A
B
C
5
50
﹖
例3 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
┐
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
提示
D
归纳总结
┐
┐
┐
1.在Rt△ABC中,∠C=90°,BC=3,AC=3,则∠B的度数为( )
A.90° B.60° C.45° D.30°
C
随堂演练
2.在Rt△ABC中,∠C=90°,∠B=35°,AB=3,则BC的长为( )
A.3sin35° B.2cos35°
C.3cos35° D.3tan35°
C
3.在△ACB中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
C
4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)a= ,c= .(2)b=15,∠B=60°.
解:(1)∵a= ,c= ,
∴∠A=30°,
∴∠B=90°-∠A=60°.
(2)∵∠C=90°,∠B=60°,
∴∠A=30°.
∵b=15,
∴ .
图②
当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.
图①
解:∵cos∠B= ,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC=13,∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7;
∴BC的长为7或17.
当三角形的形状不确定时,一定要注意分类讨论.
5. 在△ABC中,AB= ,AC=13,cos∠B= ,求BC的长.
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
课堂小结
随堂演练
1. 下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.平行四边形具有的性质矩形都具有
B
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
课堂小结
解直角
三角形
依据
勾股定理
两锐角互余
锐角的三角函数
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
第二十六章 解直角三角形
26.3 解直角三角形
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
知识回顾
定义:一般地,直角三角形中,除直角外,还有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
B
A
C
c
a
b
对边
邻边
斜边
获取新知
直角三角形中,未知的5个元素之间的关系
①三边之间的关系
B
C
A
c
b
a
已知任意两边可求出第三边
直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
已知一个锐角可求出另一个锐角
直角三角形中,未知的5个元素之间的关系
③边角之间的关系
B
C
A
c
b
a
关系式中有一角、两边三个量,已知任意两个量,可求第三个量
直角三角形中,未知的5个元素之间的关系
②两个锐角之间的关系
B
C
A
c
b
a
根据以上关系,若知道五个元素中的两个元素(至少有一个是边),就可以求出其他三个元素.
①三边之间的关系
③边角之间的关系:
例1 如图,在Rt△ABC中,∠C=90°,∠A=34°,AC=6.解这个直角三角形.(结果精确到0.01)(sin34°≈0.60,cos34°≈0.56,tan34°≈0.67)
A
C
B
34°
6
尝试独立解决,再一起交流
(1)欲求的未知元素有哪些?
∠B、BC、AB
(2)如何求∠B
利用∠A+∠B=90°
例题讲解
A
C
B
34°
6
(3)如何求BC?
所求的BC与已知的AC的比构成tanA,用tanA=BC:AC来求.
(4)如何求AB
所求的AB与已知的AC的比构成cosA,用cosA=AC:AB来求.
把所求的线段和已知的线段放到一个比例式中,确定是哪个角的哪个三角函数
sin34°≈0.60,
cos34°≈0.83,
tan34°≈0.67
A
C
B
34°
6
解:∠B=90°-∠A=90°-34°=56°.
在Rt△ABC中
∴BC=AC·tanA=6×tan34°≈6×0.6745=4.047
想一想:求AB时,用勾股定理好不好?
指明是哪个直角三角形
指明是哪个三角函数
导公式、计算
不好,会增大结果的误差,应尽可能用原题中的数据.
例2 如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到1”)
A
C
B
8
15
(1)欲求的未知元素有哪些?
∠A、∠B、AB
(2)如何求∠A
已知的BC和AC的比构成tanA,用tanA=BC:AC来求.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
A
C
B
8
15
(3)如何求∠B
(4)如何求AB
利用勾股定理.
利用∠A+∠B=90°.
例2 如图,在Rt△ABC中,∠C=90°,AC=15,BC=8.解这个直角三角形.(角度精确到1”)
A
C
B
8
解:在Rt△ABC中
∴∠A=28°
想一想:求AB时,用sinA好不好?
由边长可导出角度
不好,会增大结果的误差,应尽可能用原题中的数据.
sin28°≈0.47,
cos28°≈0.88,
tan28°≈0.53
15
∴∠B=90°-∠A=90°-28°=62°.
在Rt△ABC中,由勾股定理得
1、数形结合有利于分析问题;
2、选择关系式时,尽量使用原始数据,以防“累积误差”和“一错再错”;
3、解直角三角形时,应求出所有未知元素。
注意事项:
解直角三角形的原则:
(1)有角先求角,无角先求边
(2)有斜用弦, 无斜用切;
宁乘毋除, 取原避中。
A
B
C
5
50
﹖
例3 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC.
D
A
B
C
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD= +
┐
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
提示
D
归纳总结
┐
┐
┐
1.在Rt△ABC中,∠C=90°,BC=3,AC=3,则∠B的度数为( )
A.90° B.60° C.45° D.30°
C
随堂演练
2.在Rt△ABC中,∠C=90°,∠B=35°,AB=3,则BC的长为( )
A.3sin35° B.2cos35°
C.3cos35° D.3tan35°
C
3.在△ACB中,∠C=90°,AB=4,AC=3,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
C
4.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)a= ,c= .(2)b=15,∠B=60°.
解:(1)∵a= ,c= ,
∴∠A=30°,
∴∠B=90°-∠A=60°.
(2)∵∠C=90°,∠B=60°,
∴∠A=30°.
∵b=15,
∴ .
图②
当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.
图①
解:∵cos∠B= ,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC=13,∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7;
∴BC的长为7或17.
当三角形的形状不确定时,一定要注意分类讨论.
5. 在△ABC中,AB= ,AC=13,cos∠B= ,求BC的长.
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
课堂小结
随堂演练
1. 下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.平行四边形具有的性质矩形都具有
B
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
课堂小结
解直角
三角形
依据
勾股定理
两锐角互余
锐角的三角函数
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
