冀教版数学九年级上册同步课件:26.4 第1课时 解决与仰角、俯角及方位角有关的问题(共24张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:26.4 第1课时 解决与仰角、俯角及方位角有关的问题(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:41:36 | ||
图片预览


文档简介
(共24张PPT)
第二十六章 解直角三角形的应用
26.4 第1课时
解决与仰角、俯角及方位角有关的实际问题
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠A+ ∠B= 90 ;
(3)边角之间的关系:
(必有一边)
A
C
B
a
b
c
知识回顾
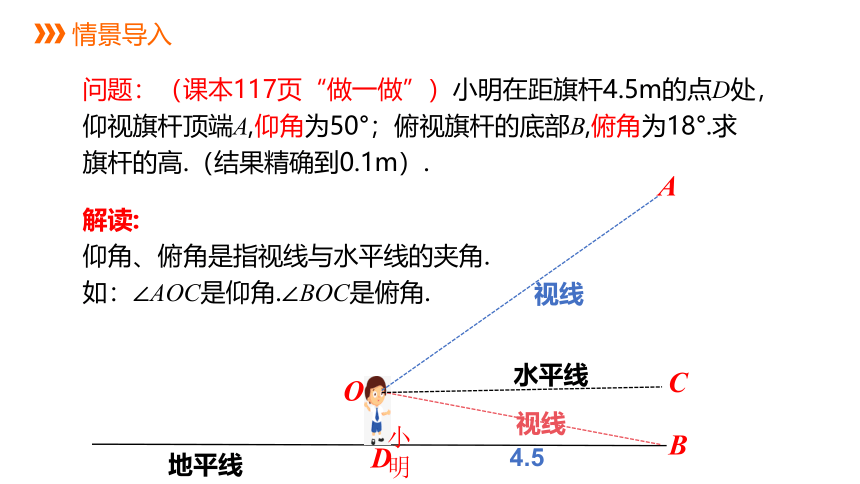
问题:(课本117页“做一做”)小明在距旗杆4.5m的点D处,仰视旗杆顶端A,仰角为50°;俯视旗杆的底部B,俯角为18°.求旗杆的高.(结果精确到0.1m).
小明
A
D
B
视线
视线
水平线
4.5
O
C
地平线
解读:
仰角、俯角是指视线与水平线的夹角.
如:∠AOC是仰角.∠BOC是俯角.
情景导入
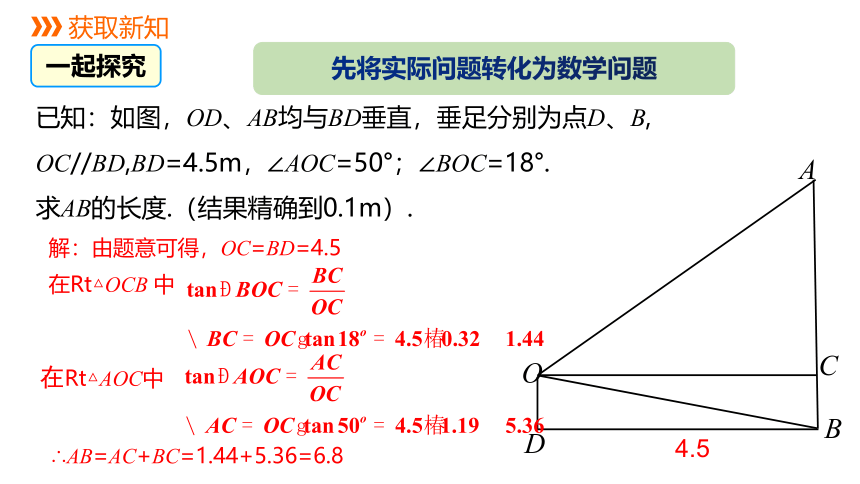
已知:如图,OD、AB均与BD垂直,垂足分别为点D、B,
OC//BD,BD=4.5m,∠AOC=50°;∠BOC=18°.
求AB的长度.(结果精确到0.1m).
先将实际问题转化为数学问题
A
D
B
4.5
O
C
获取新知
一起探究
解:由题意可得,OC=BD=4.5
在Rt△OCB 中
在Rt△AOC中
∴AB=AC+BC=1.44+5.36=6.8
东
西
北
南
O
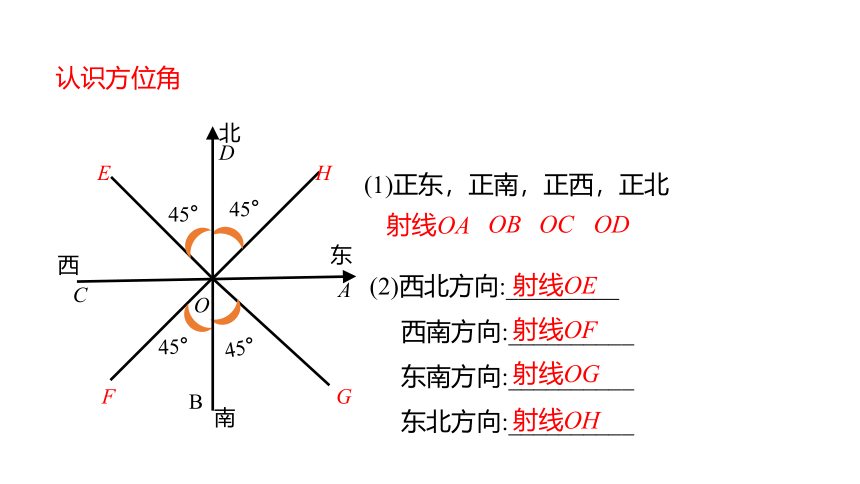
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方位角
O
北
南
西
东
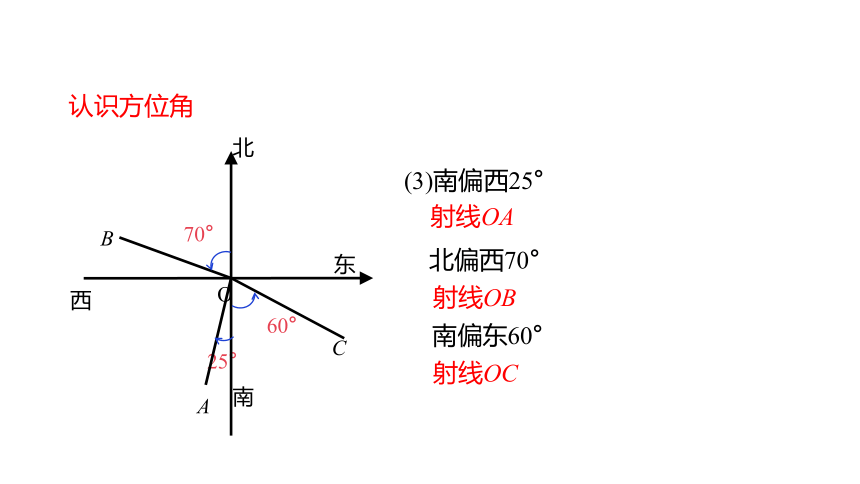
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
认识方位角
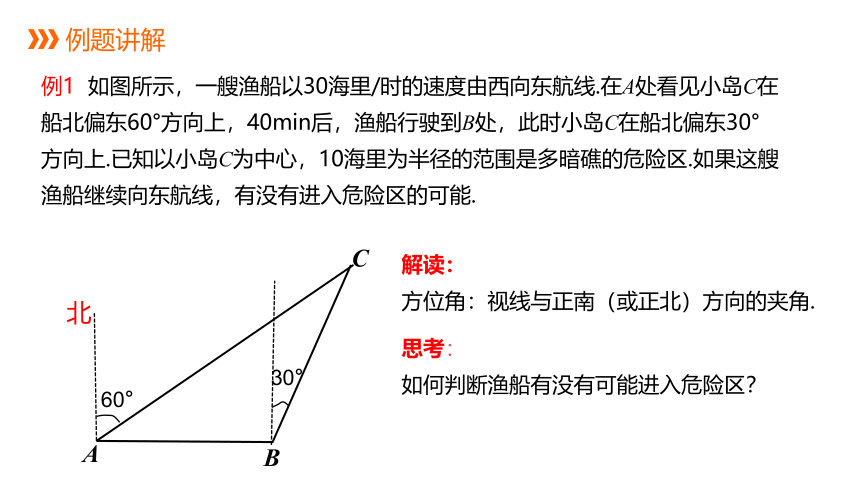
例1 如图所示,一艘渔船以30海里/时的速度由西向东航线.在A处看见小岛C在船北偏东60°方向上,40min后,渔船行驶到B处,此时小岛C在船北偏东30°方向上.已知以小岛C为中心,10海里为半径的范围是多暗礁的危险区.如果这艘渔船继续向东航线,有没有进入危险区的可能.
B
C
A
北
30°
60°
解读:
方位角:视线与正南(或正北)方向的夹角.
思考:
如何判断渔船有没有可能进入危险区?
例题讲解
B
C
A
北
30°
60°
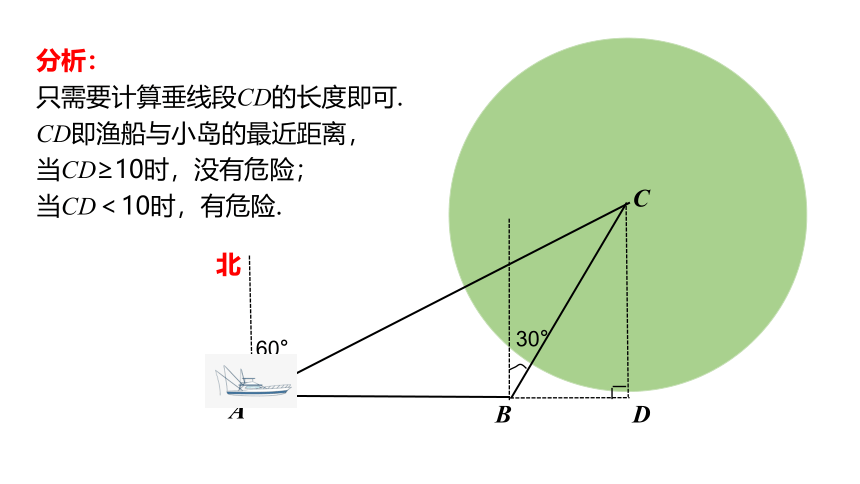
分析:
只需要计算垂线段CD的长度即可.
CD即渔船与小岛的最近距离,
当CD≥10时,没有危险;
当CD<10时,有危险.
D
B
C
A
北
30°
60°
D
E
F
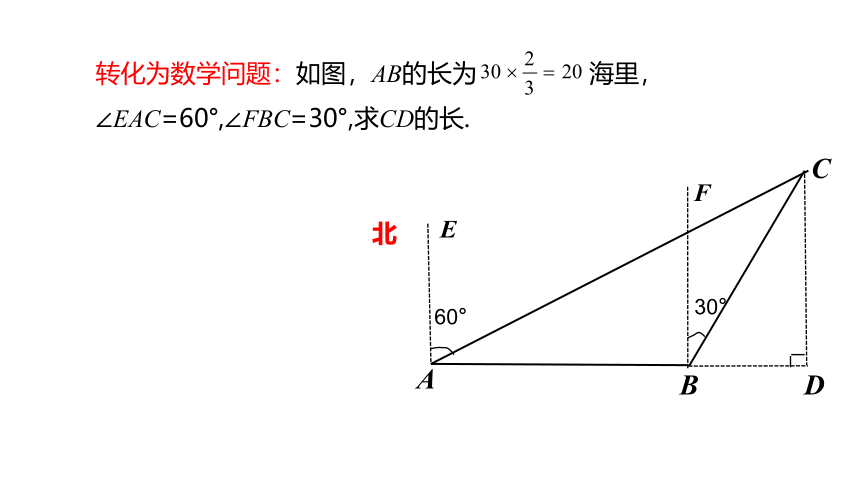
转化为数学问题:如图,AB的长为 海里,∠EAC=60°,∠FBC=30°,求CD的长.
20
B
C
A
北
30°
60°
D
E
F
方法一:
解:
过点C作CD⊥AB的延长线于点D.
则∠CBD=60°,设BD=x
在Rt△BCD中
∴CD=BD·tan∠CBD=√3x
在Rt△ACD中,
解得,x=10
∴渔船不会进入危险区.
两个直角三角形△BCD与△ACD各用一次三角函数
20
B
C
A
北
30°
60°
D
E
F
方法二:
解:
过点C作CD⊥AB的延长线于点D.
则∠CBD=60°,设CD=x
在Rt△BCD中
在Rt△ACD中,
∴渔船不会进入危险区.
两个直角三角形△BCD与△ACD各用一次三角函数
20
B
C
A
北
30°
60°
D
E
F
方法三:
解:
过点C作CD⊥AB的延长线于点D.
则∠CBD=90°-30°=60°,
∵∠1=90°-60°=30°
∴∠2=∠1=30°
∴BC=AB=20
在Rt△BCD中
∴渔船不会进入危险区.
把已知数值导入Rt△CBD中,不再用设未知数
1
2
20
B
C
A
北
30°
60°
D
E
F
20
B
C
A
北
30°
60°
D
E
F
1
2
20
思考:用三角函数求边长,什么情况下需要设未知数、列方程?什么情况下不需要设未知数,可以直接求?
方法一、二中已知边AB不是直角三角形的边长,需设未知数.
方法三中导出BC=20,BC是直角三角形的边长,可直接计算,不设未知数.
用三角函数求边长时的注意事项
1.当给出的已知边长恰为直角三角形的边长时,可直接计算;
2.当给出的已知边长不是直角三角形的边长时,可设未知数;
3.当图形中出现两个直角三角形时,一般会用两次三角函数.
1.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6 m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5 m,则旗杆AB的高度约为______m.(精确到0.1 m,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
9.5
随堂演练
2.如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=____ 米.
100
3.如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为____海里(结果取整数).
(参考数据:sin 55°≈0.8,cos 55°≈0.6,tan 55°≈1.4)
11
4.建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中,
∴AB=AC-BC=55.2-40=15.2
答:旗杆的高度为15.2m.
5. 如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心100km为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区(参考数据: ≈1.732, ≈1.414).
200km
200km
C
解:过点P作PC⊥AB,C是垂足.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC · tan30°+PC · tan45°=200,
解得 PC≈126.8km>100km.
答:计划修筑的这条高速公路不会穿越保护区.
即 PC=200,
6. 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
课堂小结
解答含有仰角、俯角问题的方法
1.仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的;可巧记为“上仰下俯”.在测量物体的高度时,要善于将实际问题抽象为数学问题.
2. 视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度.
3.弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
解答含有方位角问题的方法
解决与方位角有关的实际问题时,必须先在每个位置中心建立方向标,然后根据方位角标出图中已知角的度数,最后在某个直角三角形内利用锐角三角函数解决问题
第二十六章 解直角三角形的应用
26.4 第1课时
解决与仰角、俯角及方位角有关的实际问题
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠A+ ∠B= 90 ;
(3)边角之间的关系:
(必有一边)
A
C
B
a
b
c
知识回顾
问题:(课本117页“做一做”)小明在距旗杆4.5m的点D处,仰视旗杆顶端A,仰角为50°;俯视旗杆的底部B,俯角为18°.求旗杆的高.(结果精确到0.1m).
小明
A
D
B
视线
视线
水平线
4.5
O
C
地平线
解读:
仰角、俯角是指视线与水平线的夹角.
如:∠AOC是仰角.∠BOC是俯角.
情景导入
已知:如图,OD、AB均与BD垂直,垂足分别为点D、B,
OC//BD,BD=4.5m,∠AOC=50°;∠BOC=18°.
求AB的长度.(结果精确到0.1m).
先将实际问题转化为数学问题
A
D
B
4.5
O
C
获取新知
一起探究
解:由题意可得,OC=BD=4.5
在Rt△OCB 中
在Rt△AOC中
∴AB=AC+BC=1.44+5.36=6.8
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方位角
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
认识方位角
例1 如图所示,一艘渔船以30海里/时的速度由西向东航线.在A处看见小岛C在船北偏东60°方向上,40min后,渔船行驶到B处,此时小岛C在船北偏东30°方向上.已知以小岛C为中心,10海里为半径的范围是多暗礁的危险区.如果这艘渔船继续向东航线,有没有进入危险区的可能.
B
C
A
北
30°
60°
解读:
方位角:视线与正南(或正北)方向的夹角.
思考:
如何判断渔船有没有可能进入危险区?
例题讲解
B
C
A
北
30°
60°
分析:
只需要计算垂线段CD的长度即可.
CD即渔船与小岛的最近距离,
当CD≥10时,没有危险;
当CD<10时,有危险.
D
B
C
A
北
30°
60°
D
E
F
转化为数学问题:如图,AB的长为 海里,∠EAC=60°,∠FBC=30°,求CD的长.
20
B
C
A
北
30°
60°
D
E
F
方法一:
解:
过点C作CD⊥AB的延长线于点D.
则∠CBD=60°,设BD=x
在Rt△BCD中
∴CD=BD·tan∠CBD=√3x
在Rt△ACD中,
解得,x=10
∴渔船不会进入危险区.
两个直角三角形△BCD与△ACD各用一次三角函数
20
B
C
A
北
30°
60°
D
E
F
方法二:
解:
过点C作CD⊥AB的延长线于点D.
则∠CBD=60°,设CD=x
在Rt△BCD中
在Rt△ACD中,
∴渔船不会进入危险区.
两个直角三角形△BCD与△ACD各用一次三角函数
20
B
C
A
北
30°
60°
D
E
F
方法三:
解:
过点C作CD⊥AB的延长线于点D.
则∠CBD=90°-30°=60°,
∵∠1=90°-60°=30°
∴∠2=∠1=30°
∴BC=AB=20
在Rt△BCD中
∴渔船不会进入危险区.
把已知数值导入Rt△CBD中,不再用设未知数
1
2
20
B
C
A
北
30°
60°
D
E
F
20
B
C
A
北
30°
60°
D
E
F
1
2
20
思考:用三角函数求边长,什么情况下需要设未知数、列方程?什么情况下不需要设未知数,可以直接求?
方法一、二中已知边AB不是直角三角形的边长,需设未知数.
方法三中导出BC=20,BC是直角三角形的边长,可直接计算,不设未知数.
用三角函数求边长时的注意事项
1.当给出的已知边长恰为直角三角形的边长时,可直接计算;
2.当给出的已知边长不是直角三角形的边长时,可设未知数;
3.当图形中出现两个直角三角形时,一般会用两次三角函数.
1.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6 m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5 m,则旗杆AB的高度约为______m.(精确到0.1 m,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
9.5
随堂演练
2.如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=____ 米.
100
3.如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为____海里(结果取整数).
(参考数据:sin 55°≈0.8,cos 55°≈0.6,tan 55°≈1.4)
11
4.建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中,
∴AB=AC-BC=55.2-40=15.2
答:旗杆的高度为15.2m.
5. 如图所示,A、B两城市相距200km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心100km为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区(参考数据: ≈1.732, ≈1.414).
200km
200km
C
解:过点P作PC⊥AB,C是垂足.
则∠APC=30°,∠BPC=45°,
AC=PC·tan30°,BC=PC·tan45°.
∵AC+BC=AB,
∴PC · tan30°+PC · tan45°=200,
解得 PC≈126.8km>100km.
答:计划修筑的这条高速公路不会穿越保护区.
即 PC=200,
6. 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
课堂小结
解答含有仰角、俯角问题的方法
1.仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的;可巧记为“上仰下俯”.在测量物体的高度时,要善于将实际问题抽象为数学问题.
2. 视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度.
3.弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
解答含有方位角问题的方法
解决与方位角有关的实际问题时,必须先在每个位置中心建立方向标,然后根据方位角标出图中已知角的度数,最后在某个直角三角形内利用锐角三角函数解决问题
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
