冀教版数学九年级上册同步课件:27.2 第1课时 反比例函数的图像(共17张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:27.2 第1课时 反比例函数的图像(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 192.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:42:57 | ||
图片预览




文档简介
(共17张PPT)
27.2 第1课时 反比例函数的图像
第二十七章 反比例函数
知识回顾
1.我们学习一次函数时,研究了函数的哪些内容 是如何进行研究的
我们研究了函数的解析式、图象、性质,根据解析式,通过列表、描点、连线画出函数图象,从图象的形状、位置、增减性等多个方面分析归纳函数的性质.
2.画函数图象的一般方法和步骤是怎样的
列表、描点、连线
获取新知
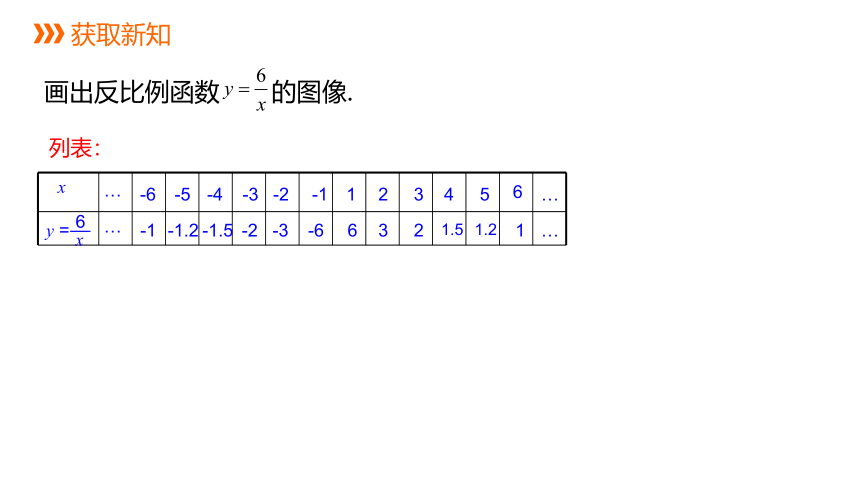
画出反比例函数 的图像.
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
列表:
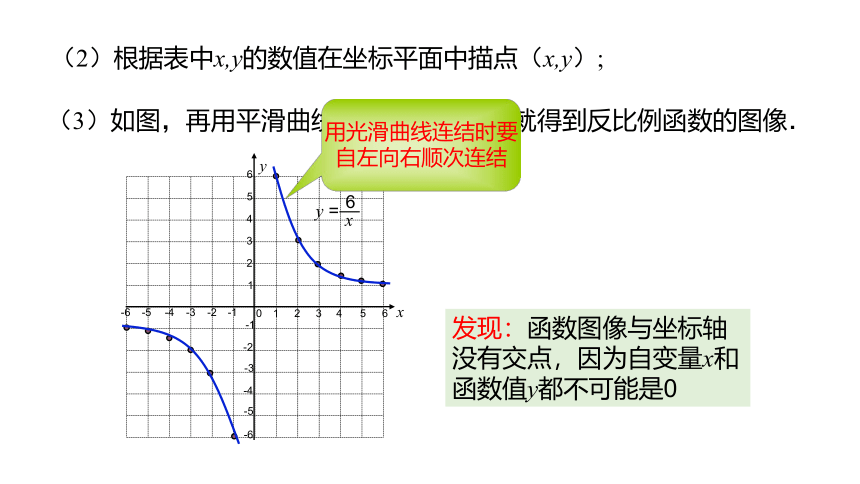
(2)根据表中x,y的数值在坐标平面中描点(x,y);
(3)如图,再用平滑曲线顺次连接各点,就得到反比例函数的图像.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
y =
x
6
发现:函数图像与坐标轴没有交点,因为自变量x和函数值y都不可能是0
用光滑曲线连结时要
自左向右顺次连结
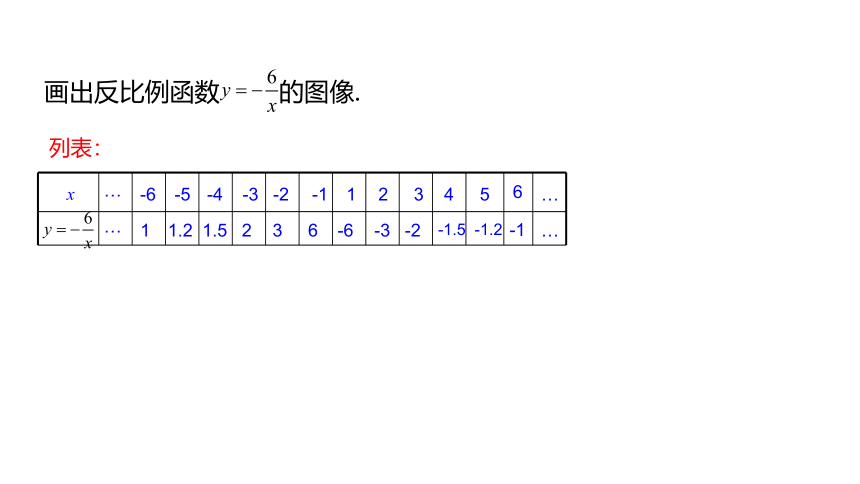
画出反比例函数 的图像.
x
1
-6
2
-3
3
-2
4
-1.5
5
-1.2
6
-1
-1
6
-2
3
-3
1.5
2
-4
-5
1.2
-6
1
…
…
…
…
列表:
(2)根据表中x,y的数值在坐标平面中描点(x,y);
(3)如图,再用平滑曲线顺次连接各点,就得到反比例函数的图像.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
y =
x
6
形状:
反比例函数 的图像是由两条曲线组成的.因此称反比例函数的图像为双曲线.
位置:
函数 的两条曲线分别位于第一、三象限内.
函数 的两条曲线分别位于第二、四象限内.
特征:
双曲线既是一个轴对称图形又是一个中心对称图形.
对称轴有两条,分别是直线y=x与直线y=-x;
对称中心是坐标原点,任何一条经过原点的直线只要
与双曲线有两个交点,则这两个交点关于原点对称.
例题讲解
例 已知点P(-6,8)在反比例函数 的图像上.
(1)求这个反比例函数的表达式.
(2)判断点M(4,-12)和N(2,24)是否在这个反比例函数的图像上.
解:(1)把点P(-6,8)的坐标代入 ,得 .
解得k=-48.
所以这个反比例函数的表达式为 .
(2)当x=4时,
当x=2时, =-24≠24.
所以,点M(4,-12)在这个反比例函数的图像上,点N(2,24)不在这个反比例函数的图像上.
3.如何判断点是否在反比例函数图像上
1.函数图像上点的坐标与函数表达式之间的关系是什么
(函数图像上的点的坐标满足函数表达式,
反之,满足函数表达式的点在该函数图像上)
2.待定系数法求反比例函数表达式时,需要几个点的坐标代入
(反比例函数中有一个待定系数,所以将函数图像上一个点的坐标代入即可)
(将点的坐标代入函数表达式,
满足函数表达式,则该点在函数图像上,
反之,则不在函数图像上)
随堂演练
1. 反比例函数 的图象大致是 ( )
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
C
2. 点(2,-4)在反比例函数 的图像上,则下列各点在此函数图像上的是( )
A.(2,4)
B.(-1,-8)
C.(-2,-4)
D.(4,-2)
D
3. 已知某种品牌电脑的显示器的寿命大约为2×104时,这种显示器工作的天数为d(天),平均每天工作的时间为t(时),那么能正确表示d与t之间的函数关系图像的是( )
C
4. 已知反比例函数 的图象在第一、三象
限内,则m的取值范围是________.
m>2
5. 如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y= 与y=- 的图像均与正方形ABCD的边相交,则图中阴影部分的面积之和是____
8
6.已知反比例函数 .
(1)求m的值;
(2)它的图像位于哪些象限
解:(1)依题意可得:m2-10=-1,且m-3≠0,
解得m=-3.
(2)当m=-3时,代入函数表达式,得 ;
∴它的图像位于第二、四象限.
课堂小结
反比例函数图像及位置:
反比例函数 表达式 图象 位置
第一、三象限
第二、四象限
反比例函数图像的位置特征:中心对称(原点);
轴对称(y=x和y=-x)
27.2 第1课时 反比例函数的图像
第二十七章 反比例函数
知识回顾
1.我们学习一次函数时,研究了函数的哪些内容 是如何进行研究的
我们研究了函数的解析式、图象、性质,根据解析式,通过列表、描点、连线画出函数图象,从图象的形状、位置、增减性等多个方面分析归纳函数的性质.
2.画函数图象的一般方法和步骤是怎样的
列表、描点、连线
获取新知
画出反比例函数 的图像.
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
列表:
(2)根据表中x,y的数值在坐标平面中描点(x,y);
(3)如图,再用平滑曲线顺次连接各点,就得到反比例函数的图像.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
y =
x
6
发现:函数图像与坐标轴没有交点,因为自变量x和函数值y都不可能是0
用光滑曲线连结时要
自左向右顺次连结
画出反比例函数 的图像.
x
1
-6
2
-3
3
-2
4
-1.5
5
-1.2
6
-1
-1
6
-2
3
-3
1.5
2
-4
-5
1.2
-6
1
…
…
…
…
列表:
(2)根据表中x,y的数值在坐标平面中描点(x,y);
(3)如图,再用平滑曲线顺次连接各点,就得到反比例函数的图像.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
y =
x
6
形状:
反比例函数 的图像是由两条曲线组成的.因此称反比例函数的图像为双曲线.
位置:
函数 的两条曲线分别位于第一、三象限内.
函数 的两条曲线分别位于第二、四象限内.
特征:
双曲线既是一个轴对称图形又是一个中心对称图形.
对称轴有两条,分别是直线y=x与直线y=-x;
对称中心是坐标原点,任何一条经过原点的直线只要
与双曲线有两个交点,则这两个交点关于原点对称.
例题讲解
例 已知点P(-6,8)在反比例函数 的图像上.
(1)求这个反比例函数的表达式.
(2)判断点M(4,-12)和N(2,24)是否在这个反比例函数的图像上.
解:(1)把点P(-6,8)的坐标代入 ,得 .
解得k=-48.
所以这个反比例函数的表达式为 .
(2)当x=4时,
当x=2时, =-24≠24.
所以,点M(4,-12)在这个反比例函数的图像上,点N(2,24)不在这个反比例函数的图像上.
3.如何判断点是否在反比例函数图像上
1.函数图像上点的坐标与函数表达式之间的关系是什么
(函数图像上的点的坐标满足函数表达式,
反之,满足函数表达式的点在该函数图像上)
2.待定系数法求反比例函数表达式时,需要几个点的坐标代入
(反比例函数中有一个待定系数,所以将函数图像上一个点的坐标代入即可)
(将点的坐标代入函数表达式,
满足函数表达式,则该点在函数图像上,
反之,则不在函数图像上)
随堂演练
1. 反比例函数 的图象大致是 ( )
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
C
2. 点(2,-4)在反比例函数 的图像上,则下列各点在此函数图像上的是( )
A.(2,4)
B.(-1,-8)
C.(-2,-4)
D.(4,-2)
D
3. 已知某种品牌电脑的显示器的寿命大约为2×104时,这种显示器工作的天数为d(天),平均每天工作的时间为t(时),那么能正确表示d与t之间的函数关系图像的是( )
C
4. 已知反比例函数 的图象在第一、三象
限内,则m的取值范围是________.
m>2
5. 如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y= 与y=- 的图像均与正方形ABCD的边相交,则图中阴影部分的面积之和是____
8
6.已知反比例函数 .
(1)求m的值;
(2)它的图像位于哪些象限
解:(1)依题意可得:m2-10=-1,且m-3≠0,
解得m=-3.
(2)当m=-3时,代入函数表达式,得 ;
∴它的图像位于第二、四象限.
课堂小结
反比例函数图像及位置:
反比例函数 表达式 图象 位置
第一、三象限
第二、四象限
反比例函数图像的位置特征:中心对称(原点);
轴对称(y=x和y=-x)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
