冀教版数学九年级上册同步课件:26.4 第2课时 解决与坡角坡度有关问题(共18张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:26.4 第2课时 解决与坡角坡度有关问题(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 757.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 14:45:26 | ||
图片预览




文档简介
(共18张PPT)
第二十六章 解直角三角形
26.4 第2课时 解决与坡角、坡度有关的问题
知识回顾
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
看一看:观察下图中的事物,了解它们的应用规律。
根据人体工程学原理,设计出合适高度的高跟鞋,满足女性爱美需求的同时,保证穿着者享受舒适的穿着体验
11°
情景导入
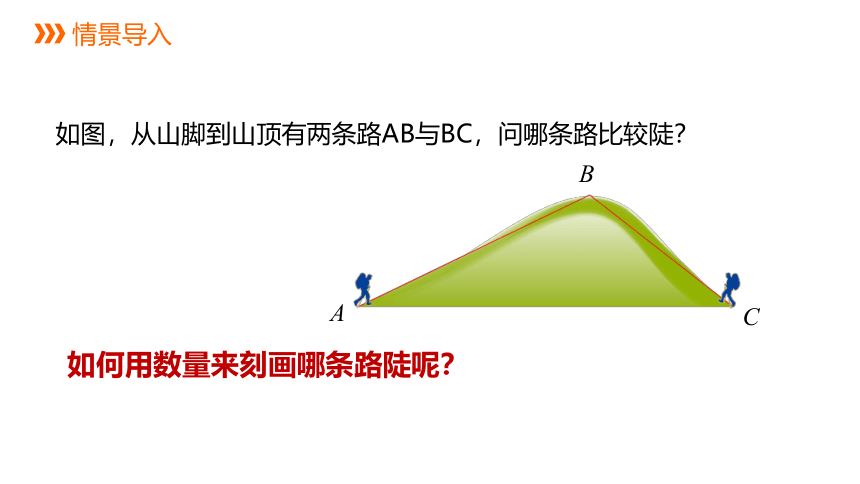
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
情景导入
坡面
α
l
h
i= h : l
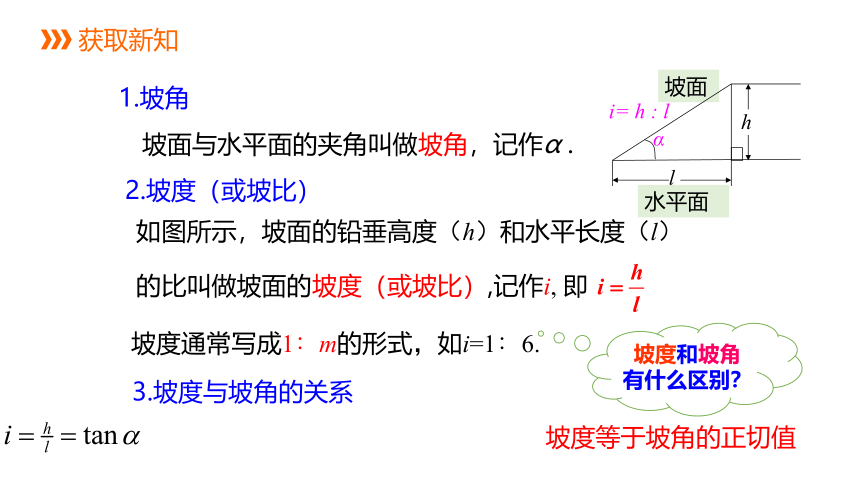
1.坡角
坡面与水平面的夹角叫做坡角,记作α .
2.坡度(或坡比)
坡度通常写成1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即
3.坡度与坡角的关系
坡度等于坡角的正切值
水平面
获取新知
坡度和坡角有什么区别?
例1 如图,一山坡的坡度为 i=1:2.小刚从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
A
C
i=1:2
解:用α表示坡角的大小,由题意可得
,因此 α≈26.57°.
在Rt△ABC中,
∠B=90°,∠A=26.57°,AC=240m,
BC=240×sin26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
例题讲解
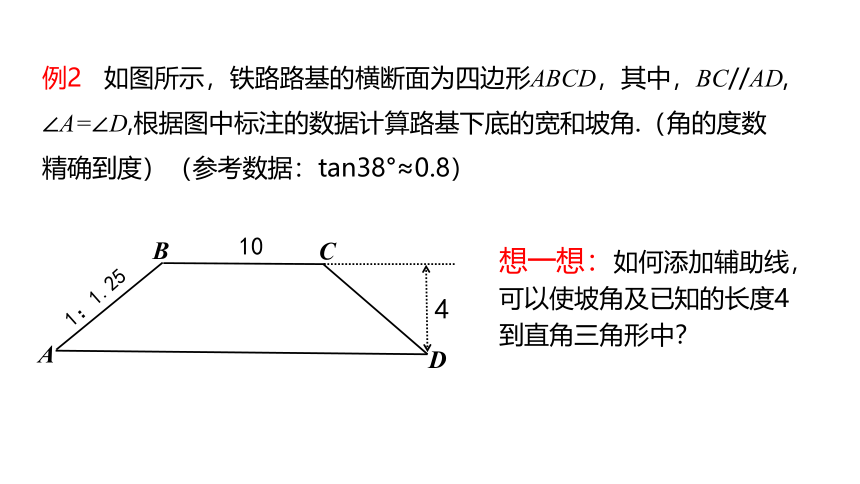
例2 如图所示,铁路路基的横断面为四边形ABCD,其中,BC//AD,
∠A=∠D,根据图中标注的数据计算路基下底的宽和坡角.(角的度数精确到度)(参考数据:tan38°≈0.8)
B
C
A
D
10
1:1.25
4
想一想:如何添加辅助线,可以使坡角及已知的长度4到直角三角形中?
B
C
A
D
10
1:1.25
4
解:如图,作BE⊥AD,CF⊥AD,垂足分别为E,F.
由题意可知,四边形BEFC为矩形.
∴EF=BC=10,BE=CF=4
F
E
∵∠A=∠D,∠BEA=∠CFD,BE=CF
∴△ABE≌△DCF
∴AE=DF
在Rt△ABE中,
∴α=38°
AE=BE÷0.8=5
∴AD=AE+EF+FD=5+10+5=20
答:路基下底的宽为20m,坡角α约为38°.
(1)若新坡角为α,求坡角α的度数.
B
C
A
P
1:1
M
1:√3
例2 某地的一座人行天桥如图所示,天桥高为6m,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8m处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡度为1:√3.
(参考数据: )
D
(2)有关部门规定,文化墙距天桥底部小于3m时应拆除,天桥改造后,该文化墙PM是否需要拆除?
B
C
A
P
1:1
M
1:√3
D
6
分析:PM是否需要拆除,要看AP的长度是否超过3m,解题的关键就转化为求线段PA的长度.
在Rt△BCD中,由tan∠BCD=1:1,
可得,BD=CD=6.
在Rt△ACD中,由tan∠CAD=1:√3,
可得,AD=√3CD=6√3≈10.4
PD=PB+BD=8+6=14
PA=PD-AD=14-10.4≈3.6>3
∴文化墙PM不需要拆除.
1.某水库堤坝的横断面如图所示,迎水坡AB的坡度是1∶3,堤坝高BC=50 m,则AB=____m.
100
随堂演练
2.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了______米.
(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
280
3.某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图,已知原阶梯式自动扶梯AB长为10 m,坡角∠ABD=30°,改造后的斜坡式自动扶梯的坡角∠ACB=15°,请你计算改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1 m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
答:改造后的斜坡式自动扶梯AC的长度约为19.2 m.
解:在Rt△ABD中,
∵∠ABD=30°,AB=10 m,
∴AD=AB·sin∠ABD=10×sin30°=5(m).
在Rt△ACD中,
∵∠ACD=15°,
∴AC=ADsin∠ACD=5sin15°≈50.26≈19.2(m).
4.水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
(1) 斜坡CD的坡角α (精确到 1°);
A
D
B
C
i=1:2.5
23
6
α
解: 斜坡CD的坡度i = tanα = 1 : 2.5=0.4,
由计算器可算得α≈22°.
故斜坡CD的坡角α 为22°.
(2) 坝底AD与斜坡AB的长度 (精确到0.1m).
解:分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知BE=CF=23m, EF=BC=6m.
在Rt△ABE中,
E
F
A
D
B
C
i=1:2.5
23
6
α
i=1:3
∴AE=3BE=3×23=69(m)
在Rt△DCF中,同理可得
在Rt△ABE中,由勾股定理可得
故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.
E
F
A
D
B
C
i=1:2.5
23
6
α
i=1:3
FD=2.5CF=2.5×23=57.5(m)
∴AD=AE+EF+FD=69+6+57.5=132.5(m)
课堂小结
与坡度有关的问题
坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i
坡面与水平面的夹角叫做坡角
第二十六章 解直角三角形
26.4 第2课时 解决与坡角、坡度有关的问题
知识回顾
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
看一看:观察下图中的事物,了解它们的应用规律。
根据人体工程学原理,设计出合适高度的高跟鞋,满足女性爱美需求的同时,保证穿着者享受舒适的穿着体验
11°
情景导入
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
情景导入
坡面
α
l
h
i= h : l
1.坡角
坡面与水平面的夹角叫做坡角,记作α .
2.坡度(或坡比)
坡度通常写成1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即
3.坡度与坡角的关系
坡度等于坡角的正切值
水平面
获取新知
坡度和坡角有什么区别?
例1 如图,一山坡的坡度为 i=1:2.小刚从山脚A出发, 沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?
A
C
i=1:2
解:用α表示坡角的大小,由题意可得
,因此 α≈26.57°.
在Rt△ABC中,
∠B=90°,∠A=26.57°,AC=240m,
BC=240×sin26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
例题讲解
例2 如图所示,铁路路基的横断面为四边形ABCD,其中,BC//AD,
∠A=∠D,根据图中标注的数据计算路基下底的宽和坡角.(角的度数精确到度)(参考数据:tan38°≈0.8)
B
C
A
D
10
1:1.25
4
想一想:如何添加辅助线,可以使坡角及已知的长度4到直角三角形中?
B
C
A
D
10
1:1.25
4
解:如图,作BE⊥AD,CF⊥AD,垂足分别为E,F.
由题意可知,四边形BEFC为矩形.
∴EF=BC=10,BE=CF=4
F
E
∵∠A=∠D,∠BEA=∠CFD,BE=CF
∴△ABE≌△DCF
∴AE=DF
在Rt△ABE中,
∴α=38°
AE=BE÷0.8=5
∴AD=AE+EF+FD=5+10+5=20
答:路基下底的宽为20m,坡角α约为38°.
(1)若新坡角为α,求坡角α的度数.
B
C
A
P
1:1
M
1:√3
例2 某地的一座人行天桥如图所示,天桥高为6m,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8m处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡度为1:√3.
(参考数据: )
D
(2)有关部门规定,文化墙距天桥底部小于3m时应拆除,天桥改造后,该文化墙PM是否需要拆除?
B
C
A
P
1:1
M
1:√3
D
6
分析:PM是否需要拆除,要看AP的长度是否超过3m,解题的关键就转化为求线段PA的长度.
在Rt△BCD中,由tan∠BCD=1:1,
可得,BD=CD=6.
在Rt△ACD中,由tan∠CAD=1:√3,
可得,AD=√3CD=6√3≈10.4
PD=PB+BD=8+6=14
PA=PD-AD=14-10.4≈3.6>3
∴文化墙PM不需要拆除.
1.某水库堤坝的横断面如图所示,迎水坡AB的坡度是1∶3,堤坝高BC=50 m,则AB=____m.
100
随堂演练
2.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了______米.
(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
280
3.某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图,已知原阶梯式自动扶梯AB长为10 m,坡角∠ABD=30°,改造后的斜坡式自动扶梯的坡角∠ACB=15°,请你计算改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1 m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
答:改造后的斜坡式自动扶梯AC的长度约为19.2 m.
解:在Rt△ABD中,
∵∠ABD=30°,AB=10 m,
∴AD=AB·sin∠ABD=10×sin30°=5(m).
在Rt△ACD中,
∵∠ACD=15°,
∴AC=ADsin∠ACD=5sin15°≈50.26≈19.2(m).
4.水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
(1) 斜坡CD的坡角α (精确到 1°);
A
D
B
C
i=1:2.5
23
6
α
解: 斜坡CD的坡度i = tanα = 1 : 2.5=0.4,
由计算器可算得α≈22°.
故斜坡CD的坡角α 为22°.
(2) 坝底AD与斜坡AB的长度 (精确到0.1m).
解:分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知BE=CF=23m, EF=BC=6m.
在Rt△ABE中,
E
F
A
D
B
C
i=1:2.5
23
6
α
i=1:3
∴AE=3BE=3×23=69(m)
在Rt△DCF中,同理可得
在Rt△ABE中,由勾股定理可得
故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.
E
F
A
D
B
C
i=1:2.5
23
6
α
i=1:3
FD=2.5CF=2.5×23=57.5(m)
∴AD=AE+EF+FD=69+6+57.5=132.5(m)
课堂小结
与坡度有关的问题
坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i
坡面与水平面的夹角叫做坡角
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
