冀教版数学九年级上册同步课件:28.2 过三点的圆 课件(共19张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:28.2 过三点的圆 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 175.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 14:19:52 | ||
图片预览


文档简介
(共19张PPT)
28.2 过三点的圆
第二十八章 圆
知识回顾
问题 构成圆的基本要素有哪些
两个条件:
圆心
半径
o
r
情景导入
假如旋转木马真如短片所说,是中国发明的,你能将旋转木马破碎的圆形底座还原,以帮助考古学家画进行深入的研究吗?
想一想:要确定一个圆必须满足什么条件
获取新知
知识点一:确定圆的条件
探索一
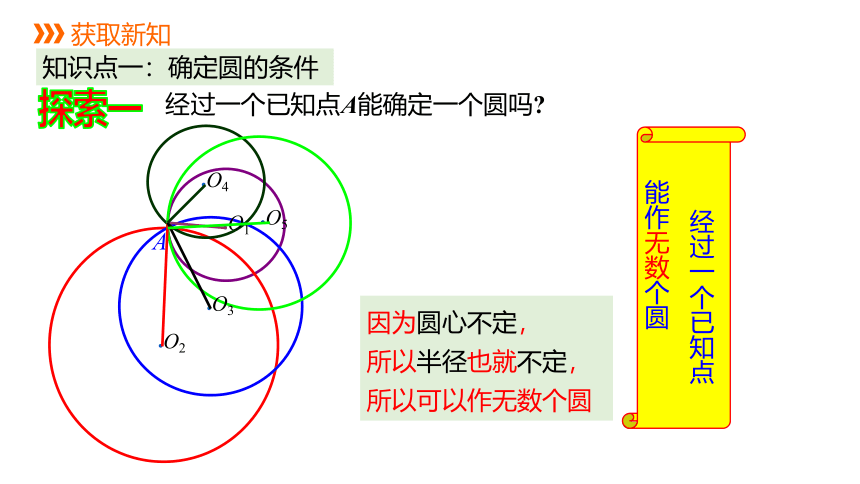
经过一个已知点A能确定一个圆吗
A
●O1
●O2
●O3
●O5
●O4
经过一个已知点
能作无数个圆
因为圆心不定,
所以半径也就不定,
所以可以作无数个圆
探索二
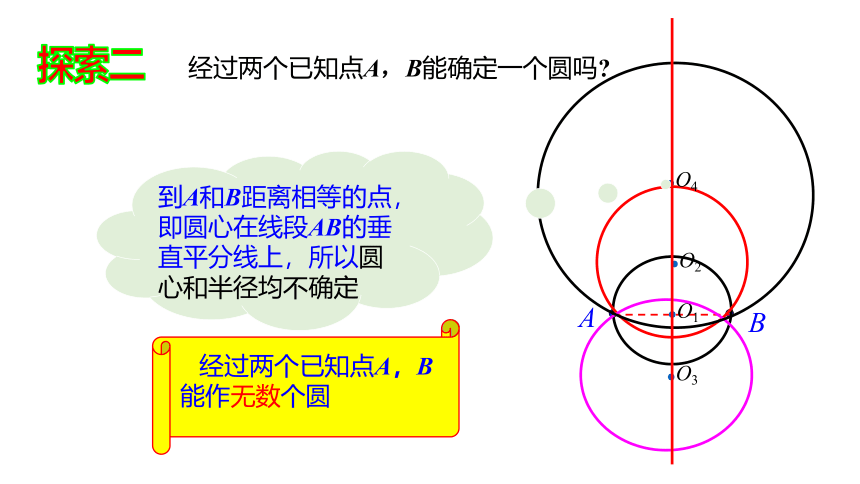
经过两个已知点A,B能确定一个圆吗
A
B
●O1
●O2
●O3
●O4
到A和B距离相等的点,即圆心在线段AB的垂直平分线上,所以圆心和半径均不确定
经过两个已知点A,B能作无数个圆
过不在同一直线上的三点A,B,C能不能确定一个圆
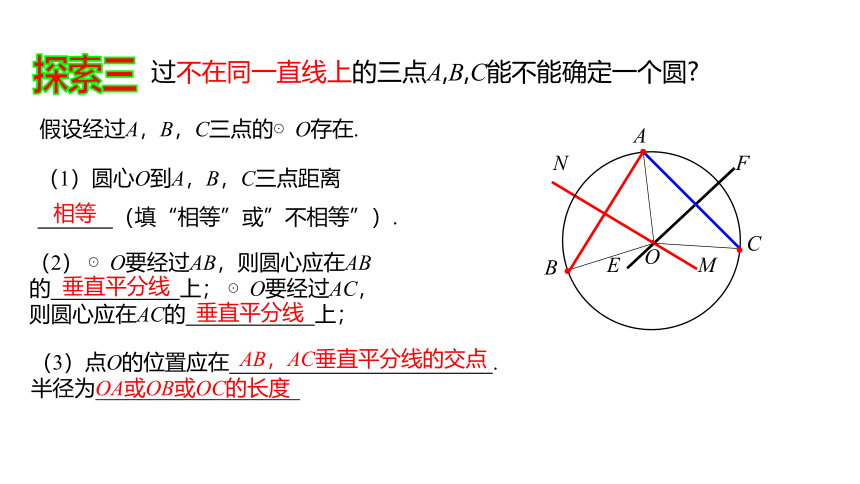
探索三
假设经过A,B,C三点的⊙O存在.
(1)圆心O到A,B,C三点距离
(填“相等”或”不相等”).
(2) ⊙O要经过AB,则圆心应在AB的 上; ⊙O要经过AC,则圆心应在AC的 上;
(3)点O的位置应在 .
半径为___________________
相等
垂直平分线
垂直平分线
AB,AC垂直平分线的交点
OA或OB或OC的长度
N
M
F
E
O
A
B
C
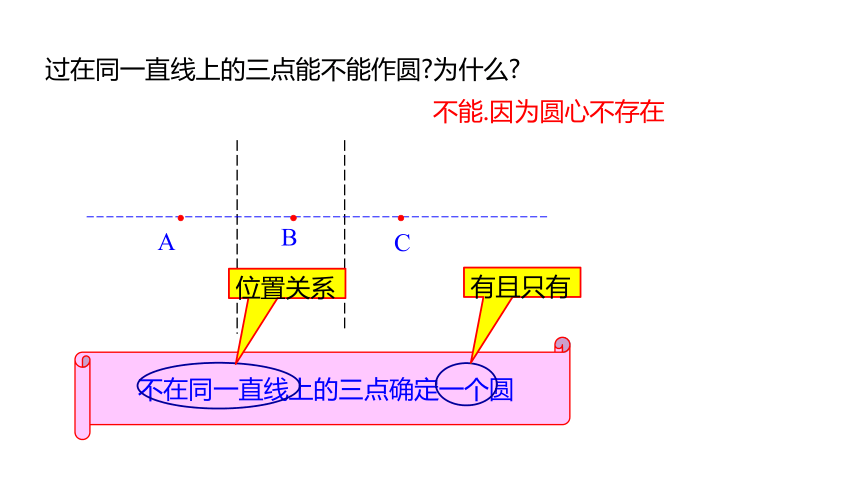
过在同一直线上的三点能不能作圆 为什么
A
B
C
不能.因为圆心不存在
不在同一直线上的三点确定一个圆
位置关系
有且只有
例题讲解
例1 用尺规作过三角形三个顶点的圆.
已知:如图所示,△ABC.
求作:☉O,使它过三点A,B,C.
解:作法:如图所示.
(1)分别作线段AB和BC的垂直平分线l1和l2.设l1与l2相交于点O.
(2)以点O为圆心,OA为半径画圆.
☉O即为所求.
l1
l2
O
获取新知
知识点二:三角形的外接圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
C
A
B
O
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
性质:三角形的外心到三角形三个顶点的距离相等.
作图:三角形三条边的垂直平分线的交点.
●O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
例2 下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;
②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内;
④三角形的外心到三角形三边的距离相等;
⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
例题讲解
B
1.三角形外心的性质:三角形的外心是它的外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各个顶点的距离相等;锐角三角形的外心在三角形的内部,直角三角形的外心是斜边的中点,钝角三角形的外心在三角形的外部.
2.三角形的外接圆有且只有一个;一个圆的内接三角形却有无数个,这些三角形的外心重合.
随堂演练
1.下列命题不正确的是( )
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
C
2.三角形的外心具有的性质是( )
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
B
C
4. 过两点A,B的圆有 个,这些圆的圆心都在线段AB的 上;过 _ 的三点的圆有且只有一个.
无数
垂直平分线
不在同一直线上
5. 如图,△ABC的外接圆的圆心坐标为 .
(6,2)
6.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
7.如图①是一个残破的圆轮,李师傅想要再浇铸一个同样大小的圆轮,你能想办法帮助李师傅吗?
解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所在的圆
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
28.2 过三点的圆
第二十八章 圆
知识回顾
问题 构成圆的基本要素有哪些
两个条件:
圆心
半径
o
r
情景导入
假如旋转木马真如短片所说,是中国发明的,你能将旋转木马破碎的圆形底座还原,以帮助考古学家画进行深入的研究吗?
想一想:要确定一个圆必须满足什么条件
获取新知
知识点一:确定圆的条件
探索一
经过一个已知点A能确定一个圆吗
A
●O1
●O2
●O3
●O5
●O4
经过一个已知点
能作无数个圆
因为圆心不定,
所以半径也就不定,
所以可以作无数个圆
探索二
经过两个已知点A,B能确定一个圆吗
A
B
●O1
●O2
●O3
●O4
到A和B距离相等的点,即圆心在线段AB的垂直平分线上,所以圆心和半径均不确定
经过两个已知点A,B能作无数个圆
过不在同一直线上的三点A,B,C能不能确定一个圆
探索三
假设经过A,B,C三点的⊙O存在.
(1)圆心O到A,B,C三点距离
(填“相等”或”不相等”).
(2) ⊙O要经过AB,则圆心应在AB的 上; ⊙O要经过AC,则圆心应在AC的 上;
(3)点O的位置应在 .
半径为___________________
相等
垂直平分线
垂直平分线
AB,AC垂直平分线的交点
OA或OB或OC的长度
N
M
F
E
O
A
B
C
过在同一直线上的三点能不能作圆 为什么
A
B
C
不能.因为圆心不存在
不在同一直线上的三点确定一个圆
位置关系
有且只有
例题讲解
例1 用尺规作过三角形三个顶点的圆.
已知:如图所示,△ABC.
求作:☉O,使它过三点A,B,C.
解:作法:如图所示.
(1)分别作线段AB和BC的垂直平分线l1和l2.设l1与l2相交于点O.
(2)以点O为圆心,OA为半径画圆.
☉O即为所求.
l1
l2
O
获取新知
知识点二:三角形的外接圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
C
A
B
O
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
性质:三角形的外心到三角形三个顶点的距离相等.
作图:三角形三条边的垂直平分线的交点.
●O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
例2 下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;
②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内;
④三角形的外心到三角形三边的距离相等;
⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
例题讲解
B
1.三角形外心的性质:三角形的外心是它的外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各个顶点的距离相等;锐角三角形的外心在三角形的内部,直角三角形的外心是斜边的中点,钝角三角形的外心在三角形的外部.
2.三角形的外接圆有且只有一个;一个圆的内接三角形却有无数个,这些三角形的外心重合.
随堂演练
1.下列命题不正确的是( )
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
C
2.三角形的外心具有的性质是( )
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
B
C
4. 过两点A,B的圆有 个,这些圆的圆心都在线段AB的 上;过 _ 的三点的圆有且只有一个.
无数
垂直平分线
不在同一直线上
5. 如图,△ABC的外接圆的圆心坐标为 .
(6,2)
6.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
7.如图①是一个残破的圆轮,李师傅想要再浇铸一个同样大小的圆轮,你能想办法帮助李师傅吗?
解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所在的圆
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
