冀教版数学九年级上册同步课件:28.3 第2课时 圆周角的概念和性质(共20张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:28.3 第2课时 圆周角的概念和性质(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 263.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 15:00:14 | ||
图片预览


文档简介
(共20张PPT)
28.3 第2课时 圆周角的概念和性质
第二十八章 圆
知识回顾
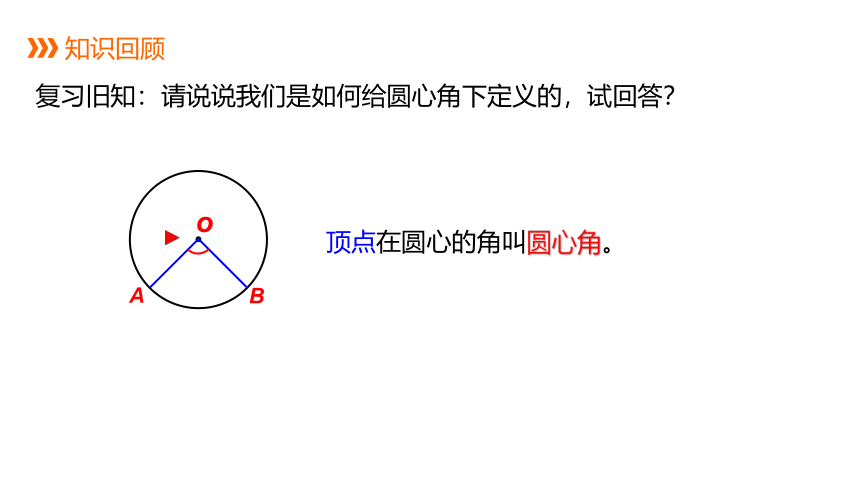
复习旧知:请说说我们是如何给圆心角下定义的,试回答?
顶点在圆心的角叫圆心角。
B
A
o
获取新知
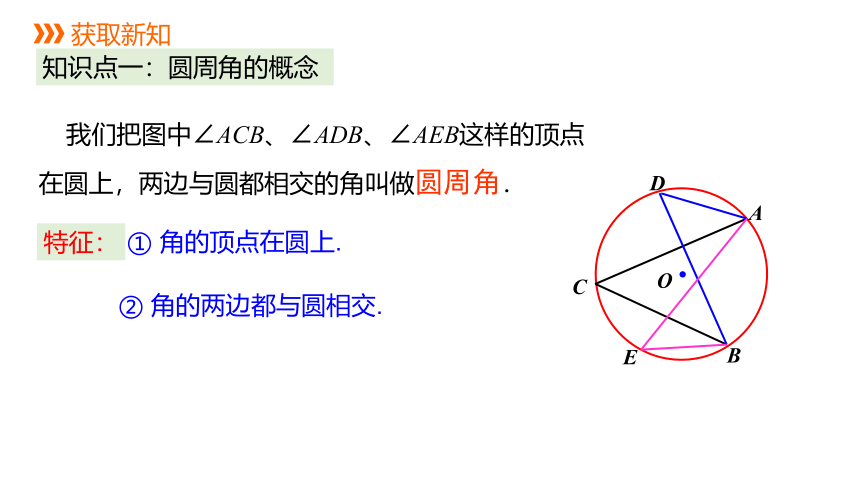
知识点一:圆周角的概念
我们把图中∠ACB、∠ADB、∠AEB这样的顶点在圆上,两边与圆都相交的角叫做圆周角.
·
A
B
C
D
E
O
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
(1)
(2)
(3)
(4)
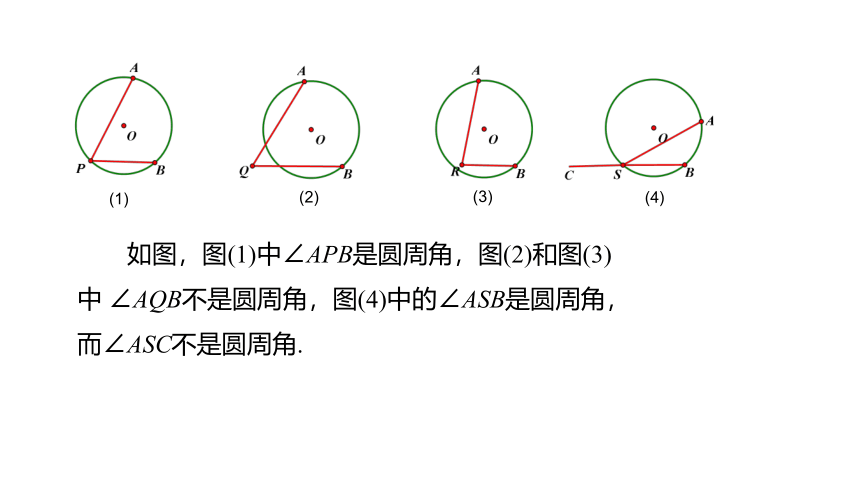
如图,图(1)中∠APB是圆周角,图(2)和图(3)中 ∠AQB不是圆周角,图(4)中的∠ASB是圆周角,而∠ASC不是圆周角.
知识点二:圆周角定理
如图,∠AOB和∠APB分别是AB所对的圆心角和圆周角.
(1)当点P在圆上按顺时针方向移动时(点P与点B不重合),按照圆心O和圆周角的位置关系,可以分为几种不同的情形?说出你的判断并画出相应的图形.
(2)当圆心O落在∠APB的一条边上时∠AOB与∠APB具有怎样的大小关系?说明理由.
(3)当圆心O在的内部和外部时,(2)中的结论还成立吗?和同学进行交流.
⌒
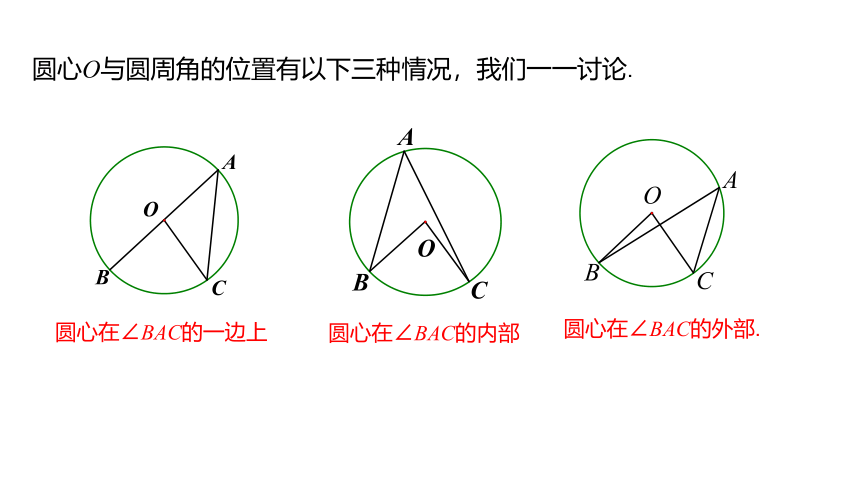
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
B
C
O
A
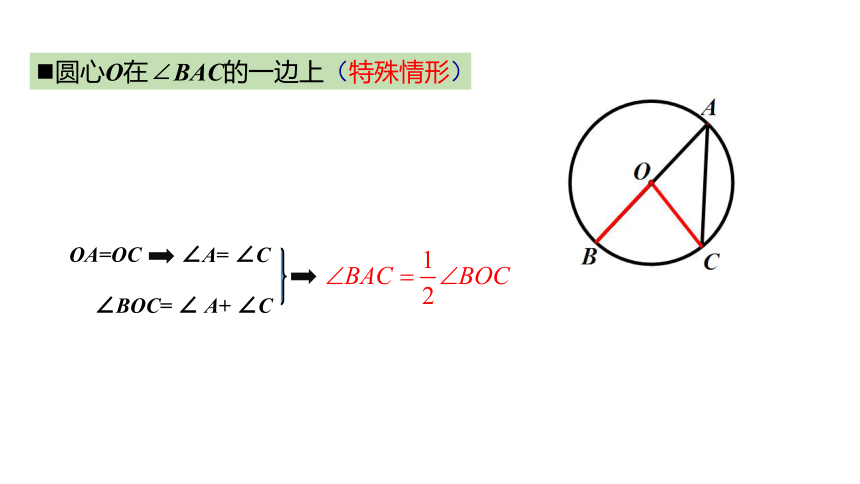
圆心在∠BAC的一边上
B
C
O
A
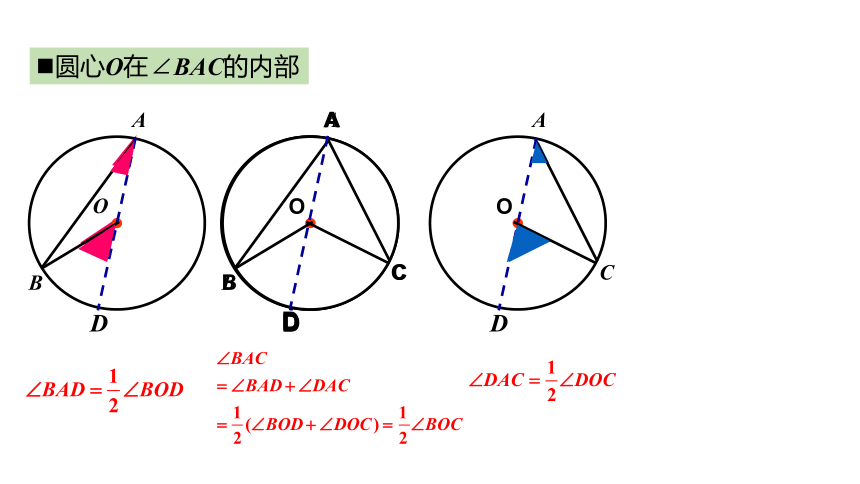
圆心在∠BAC的内部
B
C
O
A
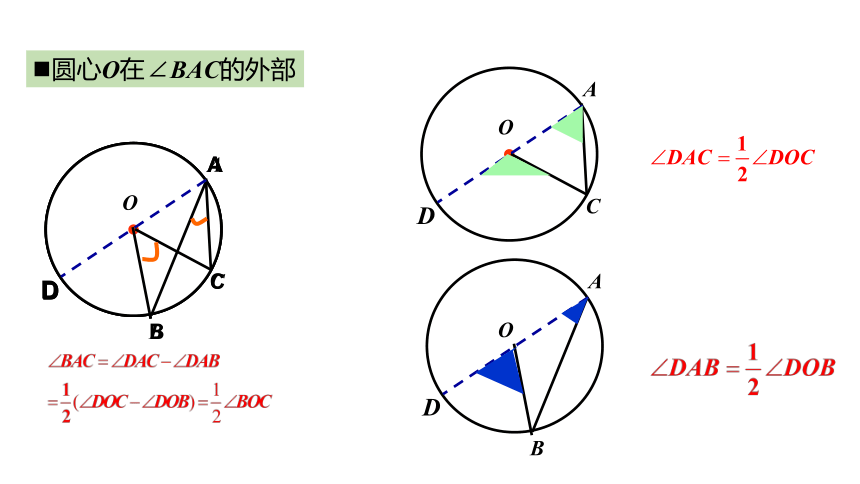
圆心在∠BAC的外部.
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
圆心O在∠BAC的内部
O
A
B
D
O
A
C
D
O
A
B
C
D
O
A
C
D
O
A
B
D
圆心O在∠BAC的外部
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
圆周角定理:
圆上一条弧所对的圆周角等于它所对的圆心角的一半
C
A
O
B
例题讲解
例1 如图 ,点 A,B,C 均在⊙O 上,∠OAB = 46°.
求∠ACB的度数.
解:如图,连接OB.
∵OA=OB,
∴∠OAB=∠OBA.
∵∠OAB =46°,
∴∠AOB= 180°-2∠OAB
=180°-2×46°= 88°.
∴∠ACB= ∠AOB= 44°.
获取新知
知识点三:圆周角与直径的关系
思考
如图,线段AB是⊙O的直径, 点C是⊙O上任意一点(除点A、B), 那么,∠ACB就是直径AB(或半圆AB)所对的圆周角.
想想看,∠ACB会是怎么样的角?
直径所对的圆周角等是直角。
反过来也是成立的,即
90°的圆周角所对的弦是直径。
理由:
1.直径所对的半圆所对的圆心角是180°;
2.圆心角是180°所对应的弦是直径;
3.圆周角等于所对弧上的圆心角的一半
圆周角定理的推论
例2 已知:如图,AB是⊙O的直径,D是圆上任意一点(不与A,B重合),连接BD并延长到点C,使BD=DC,连接AC,试判断△ABC的形状
解:如图,连接AD.
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC.
∵BD=DC,
∴AB=AC,
∴△ABC是等腰三角形.
例题讲解
随堂演练
1. 如图所示,∠BAC是圆周角的是( )
A
2.如图,△ABC是⊙O的内接三角形,若∠ABC =70°,则∠AOC的度数等于( )
A.140° B.130°
C.120° D.110°
A
O
C
B
A
3. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C. 45° D.30°
D
4.(1)将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB=_____.
25°
(2)如图所示,AB是⊙O的直径,AC、BC是⊙O的
两条弦,AB=10,∠A=30°,则BC=_____.
5
5. 如图,AB为☉O的直径,AB=AC,BC交☉O于点D,
AC交☉O于点E,∠BAC=50°,求∠EBC的度数.
解:∵AB为☉O的直径,
∴∠AEB=90°,
∴∠ABE=90°-∠BAC=90°-50°=40°.
∵AB=AC,
∴∠ABC= (180°-∠BAC)=65°,
∴∠EBC=∠ABC-∠ABE=25°.
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆上一条弧所对的圆周角等于它所对的圆心角的一半
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与
直径的关系
1.直径所对的圆周角是直角.
2.90°的圆周角所对的弦是直径;
28.3 第2课时 圆周角的概念和性质
第二十八章 圆
知识回顾
复习旧知:请说说我们是如何给圆心角下定义的,试回答?
顶点在圆心的角叫圆心角。
B
A
o
获取新知
知识点一:圆周角的概念
我们把图中∠ACB、∠ADB、∠AEB这样的顶点在圆上,两边与圆都相交的角叫做圆周角.
·
A
B
C
D
E
O
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
(1)
(2)
(3)
(4)
如图,图(1)中∠APB是圆周角,图(2)和图(3)中 ∠AQB不是圆周角,图(4)中的∠ASB是圆周角,而∠ASC不是圆周角.
知识点二:圆周角定理
如图,∠AOB和∠APB分别是AB所对的圆心角和圆周角.
(1)当点P在圆上按顺时针方向移动时(点P与点B不重合),按照圆心O和圆周角的位置关系,可以分为几种不同的情形?说出你的判断并画出相应的图形.
(2)当圆心O落在∠APB的一条边上时∠AOB与∠APB具有怎样的大小关系?说明理由.
(3)当圆心O在的内部和外部时,(2)中的结论还成立吗?和同学进行交流.
⌒
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
B
C
O
A
圆心在∠BAC的一边上
B
C
O
A
圆心在∠BAC的内部
B
C
O
A
圆心在∠BAC的外部.
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
圆心O在∠BAC的内部
O
A
B
D
O
A
C
D
O
A
B
C
D
O
A
C
D
O
A
B
D
圆心O在∠BAC的外部
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
圆周角定理:
圆上一条弧所对的圆周角等于它所对的圆心角的一半
C
A
O
B
例题讲解
例1 如图 ,点 A,B,C 均在⊙O 上,∠OAB = 46°.
求∠ACB的度数.
解:如图,连接OB.
∵OA=OB,
∴∠OAB=∠OBA.
∵∠OAB =46°,
∴∠AOB= 180°-2∠OAB
=180°-2×46°= 88°.
∴∠ACB= ∠AOB= 44°.
获取新知
知识点三:圆周角与直径的关系
思考
如图,线段AB是⊙O的直径, 点C是⊙O上任意一点(除点A、B), 那么,∠ACB就是直径AB(或半圆AB)所对的圆周角.
想想看,∠ACB会是怎么样的角?
直径所对的圆周角等是直角。
反过来也是成立的,即
90°的圆周角所对的弦是直径。
理由:
1.直径所对的半圆所对的圆心角是180°;
2.圆心角是180°所对应的弦是直径;
3.圆周角等于所对弧上的圆心角的一半
圆周角定理的推论
例2 已知:如图,AB是⊙O的直径,D是圆上任意一点(不与A,B重合),连接BD并延长到点C,使BD=DC,连接AC,试判断△ABC的形状
解:如图,连接AD.
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC.
∵BD=DC,
∴AB=AC,
∴△ABC是等腰三角形.
例题讲解
随堂演练
1. 如图所示,∠BAC是圆周角的是( )
A
2.如图,△ABC是⊙O的内接三角形,若∠ABC =70°,则∠AOC的度数等于( )
A.140° B.130°
C.120° D.110°
A
O
C
B
A
3. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C. 45° D.30°
D
4.(1)将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB=_____.
25°
(2)如图所示,AB是⊙O的直径,AC、BC是⊙O的
两条弦,AB=10,∠A=30°,则BC=_____.
5
5. 如图,AB为☉O的直径,AB=AC,BC交☉O于点D,
AC交☉O于点E,∠BAC=50°,求∠EBC的度数.
解:∵AB为☉O的直径,
∴∠AEB=90°,
∴∠ABE=90°-∠BAC=90°-50°=40°.
∵AB=AC,
∴∠ABC= (180°-∠BAC)=65°,
∴∠EBC=∠ABC-∠ABE=25°.
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆上一条弧所对的圆周角等于它所对的圆心角的一半
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与
直径的关系
1.直径所对的圆周角是直角.
2.90°的圆周角所对的弦是直径;
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
