冀教版数学九年级上册同步课件:28.5 弧长和扇形面积的计算 课件(共21张PPT)
文档属性
| 名称 | 冀教版数学九年级上册同步课件:28.5 弧长和扇形面积的计算 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 23.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 14:27:18 | ||
图片预览







文档简介
(共21张PPT)
28.5 弧长和扇形的面积的计算
第二十八章 圆
情景导入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为要保证这些弯道的“展直长度”是一样的.
问题2 怎样来计算弯道的“展直长度”?
获取新知
知识点一:弧长和扇形面积的计算
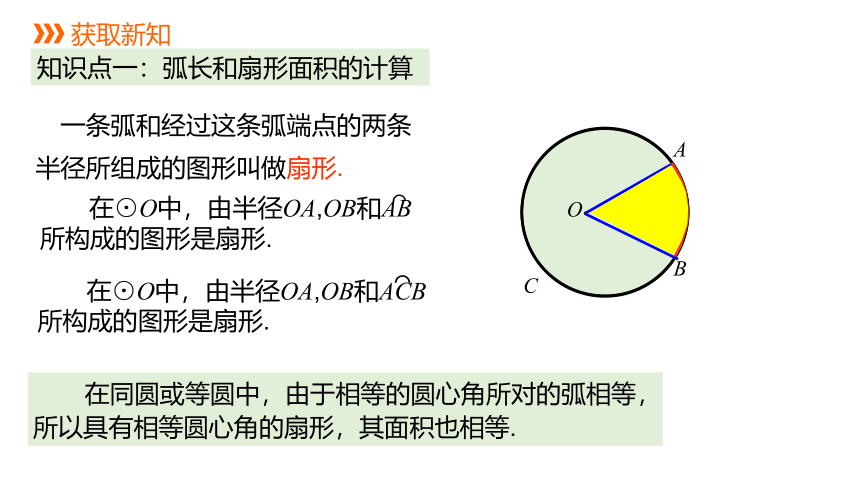
一条弧和经过这条弧端点的两条
半径所组成的图形叫做扇形.
A
B
O
C
在同圆或等圆中,由于相等的圆心角所对的弧相等,
所以具有相等圆心角的扇形,其面积也相等.
在⊙O中,由半径OA,OB和AB
所构成的图形是扇形.
⌒
在⊙O中,由半径OA,OB和ACB
所构成的图形是扇形.
⌒
弧是圆的一部分,弧长就是圆周长的一部分.在半径为R的圆中, 360 的圆心角所对的弧长就是____________.
圆周长
(1)1 的圆心角所对的弧长 l 是:
(2)n 的圆心角所对的弧长 l 是:
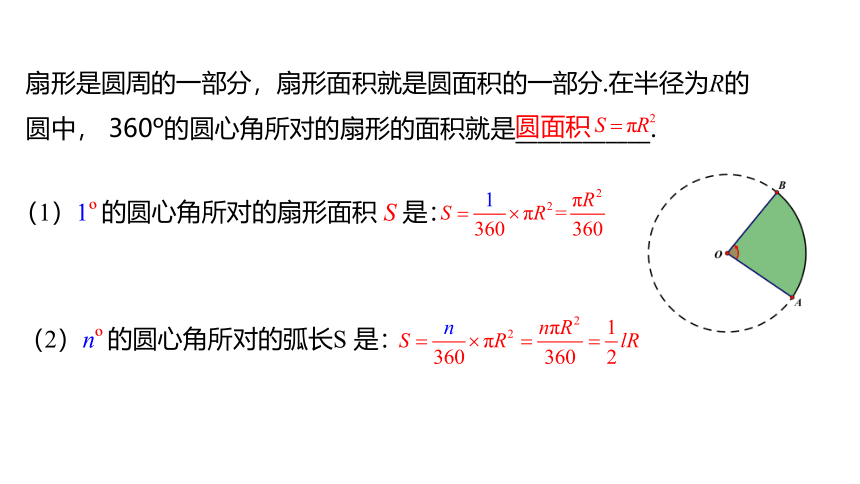
扇形是圆周的一部分,扇形面积就是圆面积的一部分.在半径为R的圆中, 360 的圆心角所对的扇形的面积就是____________.
圆面积
(1)1 的圆心角所对的扇形面积 S 是:
(2)n 的圆心角所对的弧长S 是:
弧长公式
扇形面积公式
①
②
注意:
公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;公式②也揭示弧长和扇形面积之间的关系
例题讲解
例1 如图,⊙O的半径为10 cm.
(1)如果∠AOB=100°,求AB的长及扇形AOB的面积.
(结果保留一位小数)
(2)已知BC=25 cm,求∠BOC的度数.(结果精确到1°)
⌒
⌒
解:(1) r=10 cm,∠AOB=100°,由弧长和扇形面积公式,
得
所以AB的长约为17. 4 cm,扇形AOB的面积约为87. 2 cm2.
(2)r=10 cm, =25 cm,由弧长公式,得
所以∠BOC约为143°.
⌒
获取新知
知识点二:圆锥的有关计算
圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,
侧面是一个曲面.
2.圆锥的母线(如图l)
把连接圆锥顶点和底面圆周上的任意一点的线段叫做圆锥的母线。
1.圆锥的高(如图h)
连接顶点与底面圆心的线段.
O ●
r
h
l
在△AOB中,有:__________.
l 2=r2+h2
顶点
母线
底面半径
侧面
高
圆锥的形成
把准备好的圆锥模型沿着母线剪开,观察圆锥的侧面展开图.
h
r
O
问题1:这个扇形的弧长与底面圆的周长有什么关系?
问题2:这个扇形的半径与圆锥中的哪一条线段相等
A
B
O
C
1.圆锥的侧面展开图是扇形
2.其侧面展开图扇形的半径R=母线的长l
r
h
l
3.侧面展开图扇形的弧长=底面周长
S侧=πrl(r表示圆锥底面的半径, l表示圆锥的母线长 )圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
S全=S侧+S底=πrl+πr2
L
例题讲解
例2 已知扇形的圆心角为120°,弧长为20πcm.如果用这个扇形围成一个圆锥,那么这个圆锥的侧面积是多少
∴圆锥的侧面积S= ×20π×30=300π(cm2).
解:设圆锥的母线长为l cm,由弧长公式可得:
,解得l=30.
随堂演练
1.在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π C.4π D.6π
B
2.如图,已知扇形AOB的半径为2,圆心角为90°,
连接AB,则图中阴影部分的面积是 ( )
A.π-2 B.π-4
C.4π-2 D.4π-4
A
3. 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
C
4.(1)在半径为6 cm的圆中,圆心角为60°的扇形的面积是_______;
(2)已知扇形的半径为2 cm,面积为2π cm2,则扇形的圆心角是_____;
(3)若扇形的弧长为10π cm,面积为20π cm2,则扇形的半径为_____;
(4)已知一个圆锥的底面半径为12 cm,母线长为20 cm,则这个圆锥的侧面积为______,全面积为_____.
(5)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为____.
180o
4cm
5.如图,⊙O的直径AB垂直弦CD于点E,连接BC,OC.
(1)求证:∠BCD= ∠COB;
(2)若OC=10,∠BCD=15°,求阴影部分的面积.
解:(1)证明:∵AB⊥CD,∴BC=BD.
如图,连接BD,则∠BCD=∠BDC.
∵∠COB=2∠BDC(圆周角定理),
∴∠COB=2∠BCD,
即∠BCD=∠COB.
(2)∵∠BCD=15°,∴∠COB=30°,
∴∠AOC=150°.
又∵OC=10,
6.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h.
解:由题意,得 ,而r=2cm,
∴l=6cm,
∴由勾股定理,得
即该圆锥的高h为
课堂小结
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
重要图形
重要结论
r2+h2=l2
S侧=πrl.
S 全= S侧+ S底= πrl+πr2
圆锥的高
母线
r
S
A
O
B
h
l
o
侧面
展开图
r
底面
①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
28.5 弧长和扇形的面积的计算
第二十八章 圆
情景导入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
因为要保证这些弯道的“展直长度”是一样的.
问题2 怎样来计算弯道的“展直长度”?
获取新知
知识点一:弧长和扇形面积的计算
一条弧和经过这条弧端点的两条
半径所组成的图形叫做扇形.
A
B
O
C
在同圆或等圆中,由于相等的圆心角所对的弧相等,
所以具有相等圆心角的扇形,其面积也相等.
在⊙O中,由半径OA,OB和AB
所构成的图形是扇形.
⌒
在⊙O中,由半径OA,OB和ACB
所构成的图形是扇形.
⌒
弧是圆的一部分,弧长就是圆周长的一部分.在半径为R的圆中, 360 的圆心角所对的弧长就是____________.
圆周长
(1)1 的圆心角所对的弧长 l 是:
(2)n 的圆心角所对的弧长 l 是:
扇形是圆周的一部分,扇形面积就是圆面积的一部分.在半径为R的圆中, 360 的圆心角所对的扇形的面积就是____________.
圆面积
(1)1 的圆心角所对的扇形面积 S 是:
(2)n 的圆心角所对的弧长S 是:
弧长公式
扇形面积公式
①
②
注意:
公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;公式②也揭示弧长和扇形面积之间的关系
例题讲解
例1 如图,⊙O的半径为10 cm.
(1)如果∠AOB=100°,求AB的长及扇形AOB的面积.
(结果保留一位小数)
(2)已知BC=25 cm,求∠BOC的度数.(结果精确到1°)
⌒
⌒
解:(1) r=10 cm,∠AOB=100°,由弧长和扇形面积公式,
得
所以AB的长约为17. 4 cm,扇形AOB的面积约为87. 2 cm2.
(2)r=10 cm, =25 cm,由弧长公式,得
所以∠BOC约为143°.
⌒
获取新知
知识点二:圆锥的有关计算
圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,
侧面是一个曲面.
2.圆锥的母线(如图l)
把连接圆锥顶点和底面圆周上的任意一点的线段叫做圆锥的母线。
1.圆锥的高(如图h)
连接顶点与底面圆心的线段.
O ●
r
h
l
在△AOB中,有:__________.
l 2=r2+h2
顶点
母线
底面半径
侧面
高
圆锥的形成
把准备好的圆锥模型沿着母线剪开,观察圆锥的侧面展开图.
h
r
O
问题1:这个扇形的弧长与底面圆的周长有什么关系?
问题2:这个扇形的半径与圆锥中的哪一条线段相等
A
B
O
C
1.圆锥的侧面展开图是扇形
2.其侧面展开图扇形的半径R=母线的长l
r
h
l
3.侧面展开图扇形的弧长=底面周长
S侧=πrl(r表示圆锥底面的半径, l表示圆锥的母线长 )圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
S全=S侧+S底=πrl+πr2
L
例题讲解
例2 已知扇形的圆心角为120°,弧长为20πcm.如果用这个扇形围成一个圆锥,那么这个圆锥的侧面积是多少
∴圆锥的侧面积S= ×20π×30=300π(cm2).
解:设圆锥的母线长为l cm,由弧长公式可得:
,解得l=30.
随堂演练
1.在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π C.4π D.6π
B
2.如图,已知扇形AOB的半径为2,圆心角为90°,
连接AB,则图中阴影部分的面积是 ( )
A.π-2 B.π-4
C.4π-2 D.4π-4
A
3. 圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径是( )
A.24 B.12 C.6 D.3
C
4.(1)在半径为6 cm的圆中,圆心角为60°的扇形的面积是_______;
(2)已知扇形的半径为2 cm,面积为2π cm2,则扇形的圆心角是_____;
(3)若扇形的弧长为10π cm,面积为20π cm2,则扇形的半径为_____;
(4)已知一个圆锥的底面半径为12 cm,母线长为20 cm,则这个圆锥的侧面积为______,全面积为_____.
(5)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为____.
180o
4cm
5.如图,⊙O的直径AB垂直弦CD于点E,连接BC,OC.
(1)求证:∠BCD= ∠COB;
(2)若OC=10,∠BCD=15°,求阴影部分的面积.
解:(1)证明:∵AB⊥CD,∴BC=BD.
如图,连接BD,则∠BCD=∠BDC.
∵∠COB=2∠BDC(圆周角定理),
∴∠COB=2∠BCD,
即∠BCD=∠COB.
(2)∵∠BCD=15°,∴∠COB=30°,
∴∠AOC=150°.
又∵OC=10,
6.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h.
解:由题意,得 ,而r=2cm,
∴l=6cm,
∴由勾股定理,得
即该圆锥的高h为
课堂小结
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
重要图形
重要结论
r2+h2=l2
S侧=πrl.
S 全= S侧+ S底= πrl+πr2
圆锥的高
母线
r
S
A
O
B
h
l
o
侧面
展开图
r
底面
①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
