冀教版数学八年级上册同步课件:13.3.3 利用“角边角”和“角角边”判定两个三角形全等(共34张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:13.3.3 利用“角边角”和“角角边”判定两个三角形全等(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 514.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 15:44:27 | ||
图片预览









文档简介
(共34张PPT)
第十三章 全等三角形
13.3.3 全等三角形的判定
利用“角边角”和“角角边”判定两个三角形全等
知识回顾
填一填
三sanbian相等
两边和它们夹角相等
两边和其中一边的对角相等
两角和它们的夹边相等
两角和一角的对边相等
三边对应相等
两边和它们的夹角对应相等
两边和其中一边的对角对应相等
两角和其中一角的对边对应相等
两角和它们的夹边对应相等
图形
条件
能否判定两个三角形全等
√
√
×
?
?
情景导入
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃吗?如果能,应该带哪一块去?为什么?
获取新知
知识点
判定两三角形全等的基本事实:“角边角“
1
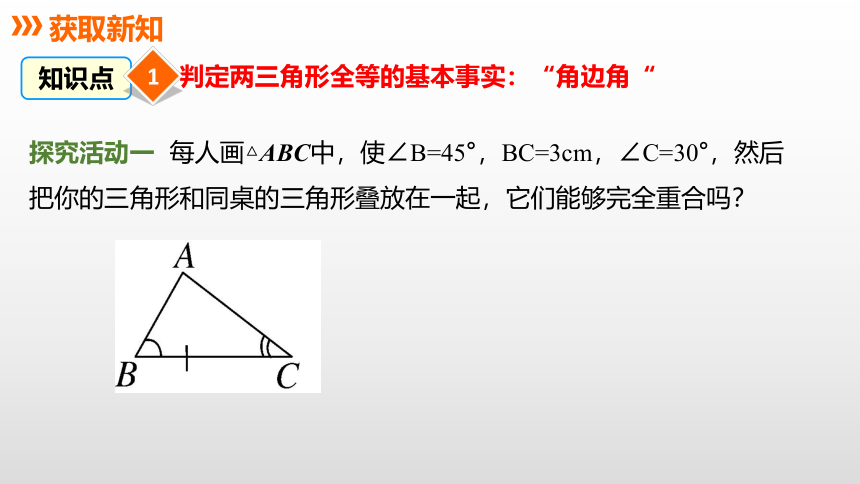
探究活动一 每人画△ABC中,使∠B=45°,BC=3cm,∠C=30°,然后把你的三角形和同桌的三角形叠放在一起,它们能够完全重合吗?
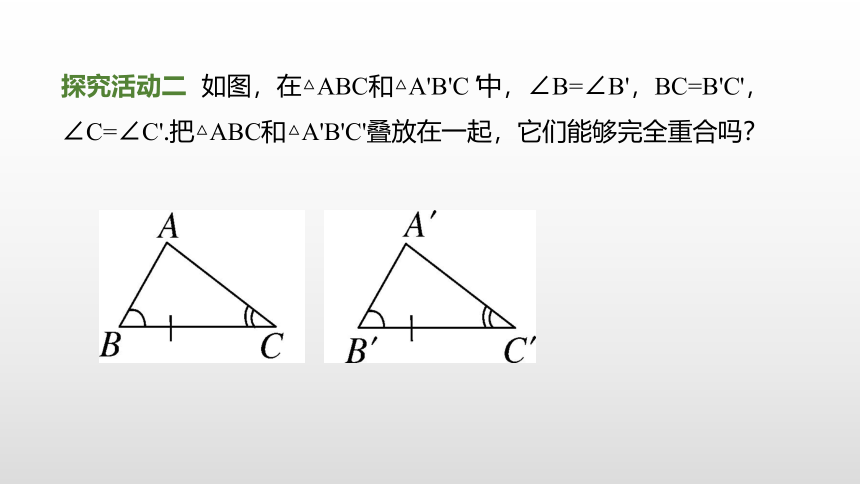
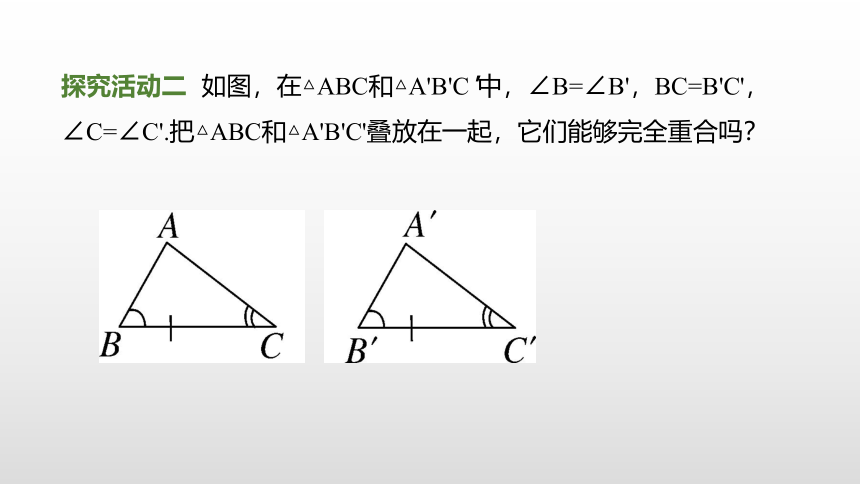
探究活动二 如图,在△ABC和△A'B'C'中,∠B=∠B',BC=B'C',∠C=∠C'.把△ABC和△A'B'C'叠放在一起,它们能够完全重合吗?
可以这样验证:
将△ABC叠放在△A′B′C′上,使边BC落在边B′C′上,顶点A与顶点A′在边B′C′的同侧.由BC=B′C′可得边BC与边B′C′完全重合.因为∠B=∠B′,∠C=∠C′ ,∠B的另一边BA落在边B′A′上, ∠C的另一边落在边C′A′上,所以∠B与∠B′完全重合, ∠C与∠C′完全重合.由于“两条直线相交只有一个交点”,所以点A与点A ′ 重合.所以, △ABC和△A′B′C′全等.
探究活动二 如图,在△ABC和△A'B'C'中,∠B=∠B',BC=B'C',∠C=∠C'.把△ABC和△A'B'C'叠放在一起,它们能够完全重合吗?
基本事实三 如果两个三角形的两个角和它们的夹边对应相等, 那么这两个三角形全等. (可简记为“角边角”或“ASA”).
归 纳
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
温馨提示:
(1)相等的元素:两角及它们的夹边;
(2)在书写两个三角形全等的条件角边角时,一定要把夹
边相等写在中间,以突出角边角的位置及对应关系.
例1 如图,AD∥BC,BE∥DF,AE=CF,
求证:△ADF≌△CBE.
解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用ASA可证明△ADF≌△CBE.
例题讲解
∴△ADF≌△CBE(ASA).
证明:∵AD∥BC,BE∥DF,(已知)
∴∠A=∠C,∠DFE=∠BEC.(两直线平行,内错角相等)
∵AE=CF,(已知)
∴AE+EF=CF+EF,即AF=CE.(等式的基本性质1)
在△ADF和△CBE中,
∠DFA=∠BEC,
AF=CE,
∠A=∠C,
已知:如图,AD=BE,∠A=∠FDE,BC∥EF.
求证:△ABC≌△DEF.
变式练习1
证明:∵ AD=BE(已知),
∴ AB=DE (等式的基本性质).
∵ BC∥EF(已知),
∴∠ABC=∠E(两直线平行,同位角相等).
在△ABC和△DEF中,
∵
∴ △ABC≌△DEF(ASA).
知识点
三角形全等的判定定理:“角角边“
2
1、如果两个三角形的两个角对应相等,那么它们的第三个角对应相等吗
2、由两个三角形的两个角和其中一个角的对边对应相等,能推出这两个三角形的全等吗?(小组讨论,并证明猜想)
探究活动三
已知:如图,在△ABC和△A′B′C′中,∠A =∠A′,∠B =∠B′, BC=B′C′.
求证: △ABC≌△A′B′C′.
证明:∵∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°,∠A=∠A′,∠B=∠B′,
∴∠A+∠B=∠A′+∠B′,∴∠C=∠C′.
∴ΔABC≌ΔA′B′C′(ASA)
在ΔABC和ΔA′B′C′中,
判定定理:如果两个三角形的两角和其中一个角的对边对应相等,那么这两个三角形全等(简记为“角角边”或“AAS”)
几何语言:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(AAS).
归纳
∠A =∠A′
∠C =∠C′
CB = C′B′
例2 如图,CA=CD,∠B=∠E,∠BCE= ∠ACD.
求证:AB=DE.
例题讲解
解析:由∠BCE=∠ACD推出∠BCA=∠ECD,然后由已知条件CA=CD,∠B=∠E,即可得出△ABC≌△DEC,即可得出AB=DE.
证明:∵∠BCE=∠ACD(已知),
∴∠BCE+∠ACE=∠ACD+∠ACE(等式的性质),
即∠BCA=∠ECD.
在△ABC和△DEC中,
∠B=∠E
∵ ∠BCA=∠ECD
CA=CD
∴△ABC≌△DEC(AAS).
∴AB=DE.
练一练 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于E.AD与BE交于F,若BF=AC,
求证:△ADC≌△BDF.
解析:先证明∠ADC=∠BDF,∠DAC=∠DBF,再由BF=AC,根据AAS即可得出两三角形全等.
∴△ADC≌△BDF(AAS).
证明:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BDF=∠BEA=90°(垂直的定义).
∵∠AFE=∠BFD(对顶角相等),
∠DAC+∠AEF+∠AFE=180°(三角形内角和定理),
∠BDF+∠BFD+∠DBF=180°(三角形内角和定理),
∴∠DAC=∠DBF.
在△ADC和△BDF中,
AC=BF,
∠DAC=∠DBF,
∠ADC=∠BDF,
证明三角形全等的“三类条件”:
(1)直接条件:即已知中直接给出的三角形的对应边或对应角.
(2)隐含条件:即已知没有给出,但通过读图得到的条件,如
公共边、公共角、对顶角.
(3)准备条件:即已知中所给条件不是三角形的对应边和对应
角,需要进一步推理.
证明三角形全等的思路:
思路一:已知两边对应相等
证明两个三角形全等,当已知两边对应相等时,通常采取下列方法:①找两边的夹角,利用“SAS”证明两个三角形全等;②找第三边,利用“SSS”证明两个三角形全等.
思路二:已知一边及其邻角对应相等
当已知一边及其邻角对应相等时:①找任意角,利用“AAS”或“ASA”证明两个三角形全等;②找夹这个角的另一条边,利用“SAS”证明两个三角形全等.切记不能用“SSA”证明两个三角形全等.
思路三 已知一边及其对角对应相等
当已知一边及其对角对应相等时,找任意角,利用“AAS”证明两个三角形全等.
思路四 已知两角对应相等
当已知两角对应相等时,通常采取下列方法:①找其中任意一角的对边,利用“AAS”证明两个三角形全等;②找两角的夹边,利用“ASA”证明两个三角形全等.
1.如图所示,亮亮书上的三角形被污染了一部分,很快他就根据所学知识画出了一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( )
A.SSS B.SAS C.AAS D.ASA
随堂演练
D
2.已知: △ABC和△ A′B′C′中,AB=A′B′, ∠A=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′的根据是( )
A. SAS B.ASA C.AAS D.都不对
B
3.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙
C.乙、丙 D.乙
C
4.如图,∠A=∠D,要使得△AOB≌△DOC,还需补充一个条件,不正确的是 ( )
A.OA=OD B.AB=DC
C.OB=OC D.∠ABO=∠DCO
D
5.如图,填空:(填“SSS”“SAS”“ASA”或“AAS”)
(1)已知BD=CE,CD=BE,利用 可以判定△BCD≌△CBE;
(2)已知AD=AE,∠ADB=∠AEC,利用 可以直接判定△ABD≌△ACE;
(3)已知OE=OD,OB=OC,利用 可以判定△BOE≌△COD;
(4)已知∠BEC=∠CDB,∠BCE=∠CBD,利用 可以直接判定△BCE≌△CBD.
SSS
ASA
ASA
AAS
6.如图,∠1=∠2,只需添加一个条件即可证明△ABC≌△BAD,这个条件可以是 (写出一个即可).
∠C=∠D或∠CAB=∠DBA或AD=BC(答案不唯一)
7.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB.
(2)若∠BDC=70°.求∠ADB的度数.
证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ABD和△ECB中,
∴△ABD≌△ECB(ASA);
(2)∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=∠CBD=40°.
8.(1)如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问(1)中的结论DE=BD+CE是否仍成立 若成立,请你给出证明;若不成立,请说明理由.
(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠AEC=90°.
∵∠BAC=90°, ∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
(2)结论DE=BD+CE仍成立.
证明:∵∠BDA=∠BAC=α,
∴∠ABD+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
课堂小结
全等三角形的判定(3)
应用
事实
定理
有两角及其中一个角的对边对应相等的两个三角形全等.
(简记为“角角边”或 “AAS”)
有两角及夹边对应相等的两个三角形全等.(简记为“角边角”或 “ASA”)
为证明线段和角的相等提供了新的方法
四种思路
第十三章 全等三角形
13.3.3 全等三角形的判定
利用“角边角”和“角角边”判定两个三角形全等
知识回顾
填一填
三sanbian相等
两边和它们夹角相等
两边和其中一边的对角相等
两角和它们的夹边相等
两角和一角的对边相等
三边对应相等
两边和它们的夹角对应相等
两边和其中一边的对角对应相等
两角和其中一角的对边对应相等
两角和它们的夹边对应相等
图形
条件
能否判定两个三角形全等
√
√
×
?
?
情景导入
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃吗?如果能,应该带哪一块去?为什么?
获取新知
知识点
判定两三角形全等的基本事实:“角边角“
1
探究活动一 每人画△ABC中,使∠B=45°,BC=3cm,∠C=30°,然后把你的三角形和同桌的三角形叠放在一起,它们能够完全重合吗?
探究活动二 如图,在△ABC和△A'B'C'中,∠B=∠B',BC=B'C',∠C=∠C'.把△ABC和△A'B'C'叠放在一起,它们能够完全重合吗?
可以这样验证:
将△ABC叠放在△A′B′C′上,使边BC落在边B′C′上,顶点A与顶点A′在边B′C′的同侧.由BC=B′C′可得边BC与边B′C′完全重合.因为∠B=∠B′,∠C=∠C′ ,∠B的另一边BA落在边B′A′上, ∠C的另一边落在边C′A′上,所以∠B与∠B′完全重合, ∠C与∠C′完全重合.由于“两条直线相交只有一个交点”,所以点A与点A ′ 重合.所以, △ABC和△A′B′C′全等.
探究活动二 如图,在△ABC和△A'B'C'中,∠B=∠B',BC=B'C',∠C=∠C'.把△ABC和△A'B'C'叠放在一起,它们能够完全重合吗?
基本事实三 如果两个三角形的两个角和它们的夹边对应相等, 那么这两个三角形全等. (可简记为“角边角”或“ASA”).
归 纳
几何语言:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
温馨提示:
(1)相等的元素:两角及它们的夹边;
(2)在书写两个三角形全等的条件角边角时,一定要把夹
边相等写在中间,以突出角边角的位置及对应关系.
例1 如图,AD∥BC,BE∥DF,AE=CF,
求证:△ADF≌△CBE.
解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用ASA可证明△ADF≌△CBE.
例题讲解
∴△ADF≌△CBE(ASA).
证明:∵AD∥BC,BE∥DF,(已知)
∴∠A=∠C,∠DFE=∠BEC.(两直线平行,内错角相等)
∵AE=CF,(已知)
∴AE+EF=CF+EF,即AF=CE.(等式的基本性质1)
在△ADF和△CBE中,
∠DFA=∠BEC,
AF=CE,
∠A=∠C,
已知:如图,AD=BE,∠A=∠FDE,BC∥EF.
求证:△ABC≌△DEF.
变式练习1
证明:∵ AD=BE(已知),
∴ AB=DE (等式的基本性质).
∵ BC∥EF(已知),
∴∠ABC=∠E(两直线平行,同位角相等).
在△ABC和△DEF中,
∵
∴ △ABC≌△DEF(ASA).
知识点
三角形全等的判定定理:“角角边“
2
1、如果两个三角形的两个角对应相等,那么它们的第三个角对应相等吗
2、由两个三角形的两个角和其中一个角的对边对应相等,能推出这两个三角形的全等吗?(小组讨论,并证明猜想)
探究活动三
已知:如图,在△ABC和△A′B′C′中,∠A =∠A′,∠B =∠B′, BC=B′C′.
求证: △ABC≌△A′B′C′.
证明:∵∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°,∠A=∠A′,∠B=∠B′,
∴∠A+∠B=∠A′+∠B′,∴∠C=∠C′.
∴ΔABC≌ΔA′B′C′(ASA)
在ΔABC和ΔA′B′C′中,
判定定理:如果两个三角形的两角和其中一个角的对边对应相等,那么这两个三角形全等(简记为“角角边”或“AAS”)
几何语言:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(AAS).
归纳
∠A =∠A′
∠C =∠C′
CB = C′B′
例2 如图,CA=CD,∠B=∠E,∠BCE= ∠ACD.
求证:AB=DE.
例题讲解
解析:由∠BCE=∠ACD推出∠BCA=∠ECD,然后由已知条件CA=CD,∠B=∠E,即可得出△ABC≌△DEC,即可得出AB=DE.
证明:∵∠BCE=∠ACD(已知),
∴∠BCE+∠ACE=∠ACD+∠ACE(等式的性质),
即∠BCA=∠ECD.
在△ABC和△DEC中,
∠B=∠E
∵ ∠BCA=∠ECD
CA=CD
∴△ABC≌△DEC(AAS).
∴AB=DE.
练一练 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于E.AD与BE交于F,若BF=AC,
求证:△ADC≌△BDF.
解析:先证明∠ADC=∠BDF,∠DAC=∠DBF,再由BF=AC,根据AAS即可得出两三角形全等.
∴△ADC≌△BDF(AAS).
证明:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BDF=∠BEA=90°(垂直的定义).
∵∠AFE=∠BFD(对顶角相等),
∠DAC+∠AEF+∠AFE=180°(三角形内角和定理),
∠BDF+∠BFD+∠DBF=180°(三角形内角和定理),
∴∠DAC=∠DBF.
在△ADC和△BDF中,
AC=BF,
∠DAC=∠DBF,
∠ADC=∠BDF,
证明三角形全等的“三类条件”:
(1)直接条件:即已知中直接给出的三角形的对应边或对应角.
(2)隐含条件:即已知没有给出,但通过读图得到的条件,如
公共边、公共角、对顶角.
(3)准备条件:即已知中所给条件不是三角形的对应边和对应
角,需要进一步推理.
证明三角形全等的思路:
思路一:已知两边对应相等
证明两个三角形全等,当已知两边对应相等时,通常采取下列方法:①找两边的夹角,利用“SAS”证明两个三角形全等;②找第三边,利用“SSS”证明两个三角形全等.
思路二:已知一边及其邻角对应相等
当已知一边及其邻角对应相等时:①找任意角,利用“AAS”或“ASA”证明两个三角形全等;②找夹这个角的另一条边,利用“SAS”证明两个三角形全等.切记不能用“SSA”证明两个三角形全等.
思路三 已知一边及其对角对应相等
当已知一边及其对角对应相等时,找任意角,利用“AAS”证明两个三角形全等.
思路四 已知两角对应相等
当已知两角对应相等时,通常采取下列方法:①找其中任意一角的对边,利用“AAS”证明两个三角形全等;②找两角的夹边,利用“ASA”证明两个三角形全等.
1.如图所示,亮亮书上的三角形被污染了一部分,很快他就根据所学知识画出了一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( )
A.SSS B.SAS C.AAS D.ASA
随堂演练
D
2.已知: △ABC和△ A′B′C′中,AB=A′B′, ∠A=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′的根据是( )
A. SAS B.ASA C.AAS D.都不对
B
3.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙
C.乙、丙 D.乙
C
4.如图,∠A=∠D,要使得△AOB≌△DOC,还需补充一个条件,不正确的是 ( )
A.OA=OD B.AB=DC
C.OB=OC D.∠ABO=∠DCO
D
5.如图,填空:(填“SSS”“SAS”“ASA”或“AAS”)
(1)已知BD=CE,CD=BE,利用 可以判定△BCD≌△CBE;
(2)已知AD=AE,∠ADB=∠AEC,利用 可以直接判定△ABD≌△ACE;
(3)已知OE=OD,OB=OC,利用 可以判定△BOE≌△COD;
(4)已知∠BEC=∠CDB,∠BCE=∠CBD,利用 可以直接判定△BCE≌△CBD.
SSS
ASA
ASA
AAS
6.如图,∠1=∠2,只需添加一个条件即可证明△ABC≌△BAD,这个条件可以是 (写出一个即可).
∠C=∠D或∠CAB=∠DBA或AD=BC(答案不唯一)
7.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB.
(2)若∠BDC=70°.求∠ADB的度数.
证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ABD和△ECB中,
∴△ABD≌△ECB(ASA);
(2)∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=∠CBD=40°.
8.(1)如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问(1)中的结论DE=BD+CE是否仍成立 若成立,请你给出证明;若不成立,请说明理由.
(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠AEC=90°.
∵∠BAC=90°, ∴∠BAD+∠CAE=90°.
∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
(2)结论DE=BD+CE仍成立.
证明:∵∠BDA=∠BAC=α,
∴∠ABD+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
课堂小结
全等三角形的判定(3)
应用
事实
定理
有两角及其中一个角的对边对应相等的两个三角形全等.
(简记为“角角边”或 “AAS”)
有两角及夹边对应相等的两个三角形全等.(简记为“角边角”或 “ASA”)
为证明线段和角的相等提供了新的方法
四种思路
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
