冀教版数学八年级上册同步课件:14.2 立方根(共28张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:14.2 立方根(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 15:57:59 | ||
图片预览








文档简介
(共28张PPT)
第十四章 实数
14.2 立方根
知识回顾
1.什么叫平方根?
2.平方根的性质有哪些?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果x2=a,那么x 叫做a的平方根.
(1)一个正数有两个平方根,它们互为相反数;
(2)0只有两平方根,是0本身;
(3)负数没有平方根.
情景导入
现在要做一个体积为8cm3的立方体魔方,它的棱要取多少长?你是怎样知道的?
体积为27cm3的立方体的棱又要取多少长?
体积为100cm3的立方体的棱又要取多少长?
思考
获取新知
知识点
立方根
1
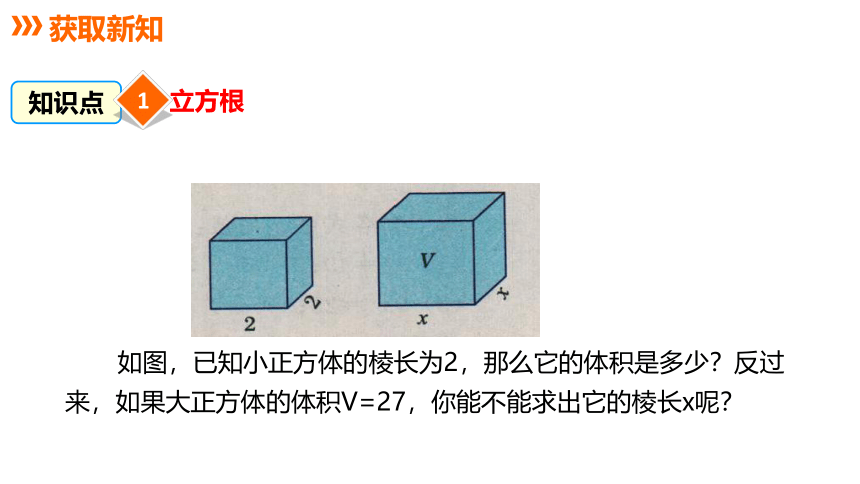
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
求满足下列各式的x的值:
(1)x3=-l;(2)x3=64;(3)x3=0.008;(4)x3 =-
小亮是这样想的:由已知小正方体的棱长为2,可
以求出它的体积为23 = 8;同样,根据正方体的体公式
以及立方运算,由大正方体的体积,也可以求出它的
棱长.
他是这样做的:因为33=27,所以,这个大正方体
的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么
做的?
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作 .
一个数a的立方根可以表示为:
根指数
被开方数
读作:三次根号 a
立方根的定义
立方根的表示
概念学习
a是被开方数,
3是根指数,
3不能省略.
-1的立方根为-1,记作
64的立方根为4,记作
0.008的立方根为0.2,记作
- 的立方根为 ,记作
例如
探究活动一
(1)根据立方根的意义填空:
因为 =8,所以8的立方根是( );
因为( )3 =0.125,所以0.125的立方是( );
因为 ( )3 =-8,所以-8的立方根是( );
因为( ) 3= ,所以 的立方( ).
0
2
-2
0
-2
(2)正数、0、负数的立方根各有什么特点?
因为( )3 =0,所以0的立方根是( );
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
立方根的性质
总结
任何有理数都有立方根,而且它的立方根是唯一的.
唯一性
同号性
平方根与立方根的区别和联系
平方根 立方根
区别 定义 一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根 一般地,如果一个数x的立方等于a,即x3=a,那么这个数x叫做a的立方根
性质 正数有两个平方根,它们互为相反数 正数有一个立方根,仍为正数
负数没有平方根 负数有一个立方根,仍为负数
表示法 ± (a≥0) (a为任意数)
联系 ①开平方与开立方都与相应的乘方运算互为逆运算 ②0的平方根和立方根都是0
例1 判断下列说法是否正确
(1) 2是8的立方根 ( )
(2)-9没有立方根 ( )
(3) ( )
(4) ( )
(5) ( )
(6)正数有两个立方根,负数没有立方根 ( )
×
×
×
√
√
√
例题讲解
知识点
求一个数的立方根
2
概念学习
类似开平方运算,求一个数的立方根的运算叫作开立方.
温馨提示:根据开立方与立方的互逆运算关系,我们可以借助立方运算求一个数的立方根.
开立方与立方互为逆运算.
例题讲解
例2 求下列各数的立方根:
(1) (2) -8; (3)-0.064.
(1)因为 ,所以 的立方根为 ,
即
(2)因为(-2)3 =-8,所以-8的立方根为-2,
即 =-2.
(3)因为(-0.4)3 =-0.064,所以-0.064的立方根
为-0.4,即 =-0. 4.
解:
因为 =____, =____,
所以 ____ ;
因为 =____, =____,
所以 ____ ;
– 2
– 2
=
– 3
– 3
=
填一填
归纳
探究活动二
例3 求下列各式的值:
解:
解析:求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.
变式练习
1 计算:
解:
例4.在做浮力实验时,小华用一根细线将一正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一量筒量得被铁块排开的水的体积为64立方厘米,小华又将铁块从烧杯中提起,量得烧杯中的水位下降了3厘米.请问烧杯内部的底面半径和铁块的棱长各是多少(π取3,结果保留整数)?
解:设正方体铁块的棱长是x厘米,烧杯内部的底面半径是r厘米,
根据题意列方程得x3=64,
解得x=4,
所以正方体铁块的棱长是4厘米.
设烧杯内部的底面半径是r厘米,根据题意列方程得
πr2×3=64,所以 .因为r>0,解得 .
所以烧杯内部的底面半径是厘米.
随堂演练
1.下列各式中,正确的是( )
A. =±2 B. =5
C. ±2 D.
2. 的算术平方根是( )
A.2 B.±2
C. D.±
C
B
3.有下列说法:①一个数的立方根有两个,它们互为相反数;②若x3=(-2)3,则x=-2;③15的立方根是 ;④任何有理数都有立方根,它不是正数就是负数.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
4.若一个数的立方根与它本身相同,则这个数是( )
A.0 B.0或1 C.0或-1 D.0或±1
B
D
5. 若 是5的立方根,则b=____,若 =-2,则a=_______.
6. 分析下列四句话:
①因为(-3)3=-27,所以-3是-27的立方根;
②因为43=64,所以64是4的立方根;
③把2立方与把8开立方互为逆运算;
④把4立方与把4开平方互为逆运算.
其中正确的是_________.(填序号)
1
-8
①③
7.填一填:
(1)1的平方根是____;立方根为____;算术平方根为____.
(2)平方根是它本身的数是____.
(3)算术平方根是其本身的数是____.
(4) 的立方根为 .
(5) 的平方根为 .
(6) 的立方根为 .
1
1
±1
0
0, 1
±2
-2
-2
(1) (2) (3)
8. 计算:
8.求下列各式的值.
(1)
(2)
(3)
(4)
= – 0.3
=
=
=
=
=
10.求下列各式中x的值:
(1)x3=-
;
(2)4(x-1)3=-256.
解:(1)x= =- .
(2)(x-1)3=-64,x-1=-4,x=-3.
11.若 =2, =4,求 的值.
解:∵ =2, =4.
∴x = 23,y2 = 16,
∴x = 8,y = ±4.
∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
∴ = = 4 或 = = 0.
课堂小结
立方根
规律
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a 的三次方根.
性质
正数的立方根是正数,
负数的立方根是负数;
0的立方根是0 .
定义
第十四章 实数
14.2 立方根
知识回顾
1.什么叫平方根?
2.平方根的性质有哪些?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果x2=a,那么x 叫做a的平方根.
(1)一个正数有两个平方根,它们互为相反数;
(2)0只有两平方根,是0本身;
(3)负数没有平方根.
情景导入
现在要做一个体积为8cm3的立方体魔方,它的棱要取多少长?你是怎样知道的?
体积为27cm3的立方体的棱又要取多少长?
体积为100cm3的立方体的棱又要取多少长?
思考
获取新知
知识点
立方根
1
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
求满足下列各式的x的值:
(1)x3=-l;(2)x3=64;(3)x3=0.008;(4)x3 =-
小亮是这样想的:由已知小正方体的棱长为2,可
以求出它的体积为23 = 8;同样,根据正方体的体公式
以及立方运算,由大正方体的体积,也可以求出它的
棱长.
他是这样做的:因为33=27,所以,这个大正方体
的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么
做的?
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作 .
一个数a的立方根可以表示为:
根指数
被开方数
读作:三次根号 a
立方根的定义
立方根的表示
概念学习
a是被开方数,
3是根指数,
3不能省略.
-1的立方根为-1,记作
64的立方根为4,记作
0.008的立方根为0.2,记作
- 的立方根为 ,记作
例如
探究活动一
(1)根据立方根的意义填空:
因为 =8,所以8的立方根是( );
因为( )3 =0.125,所以0.125的立方是( );
因为 ( )3 =-8,所以-8的立方根是( );
因为( ) 3= ,所以 的立方( ).
0
2
-2
0
-2
(2)正数、0、负数的立方根各有什么特点?
因为( )3 =0,所以0的立方根是( );
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
立方根的性质
总结
任何有理数都有立方根,而且它的立方根是唯一的.
唯一性
同号性
平方根与立方根的区别和联系
平方根 立方根
区别 定义 一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根 一般地,如果一个数x的立方等于a,即x3=a,那么这个数x叫做a的立方根
性质 正数有两个平方根,它们互为相反数 正数有一个立方根,仍为正数
负数没有平方根 负数有一个立方根,仍为负数
表示法 ± (a≥0) (a为任意数)
联系 ①开平方与开立方都与相应的乘方运算互为逆运算 ②0的平方根和立方根都是0
例1 判断下列说法是否正确
(1) 2是8的立方根 ( )
(2)-9没有立方根 ( )
(3) ( )
(4) ( )
(5) ( )
(6)正数有两个立方根,负数没有立方根 ( )
×
×
×
√
√
√
例题讲解
知识点
求一个数的立方根
2
概念学习
类似开平方运算,求一个数的立方根的运算叫作开立方.
温馨提示:根据开立方与立方的互逆运算关系,我们可以借助立方运算求一个数的立方根.
开立方与立方互为逆运算.
例题讲解
例2 求下列各数的立方根:
(1) (2) -8; (3)-0.064.
(1)因为 ,所以 的立方根为 ,
即
(2)因为(-2)3 =-8,所以-8的立方根为-2,
即 =-2.
(3)因为(-0.4)3 =-0.064,所以-0.064的立方根
为-0.4,即 =-0. 4.
解:
因为 =____, =____,
所以 ____ ;
因为 =____, =____,
所以 ____ ;
– 2
– 2
=
– 3
– 3
=
填一填
归纳
探究活动二
例3 求下列各式的值:
解:
解析:求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.
变式练习
1 计算:
解:
例4.在做浮力实验时,小华用一根细线将一正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一量筒量得被铁块排开的水的体积为64立方厘米,小华又将铁块从烧杯中提起,量得烧杯中的水位下降了3厘米.请问烧杯内部的底面半径和铁块的棱长各是多少(π取3,结果保留整数)?
解:设正方体铁块的棱长是x厘米,烧杯内部的底面半径是r厘米,
根据题意列方程得x3=64,
解得x=4,
所以正方体铁块的棱长是4厘米.
设烧杯内部的底面半径是r厘米,根据题意列方程得
πr2×3=64,所以 .因为r>0,解得 .
所以烧杯内部的底面半径是厘米.
随堂演练
1.下列各式中,正确的是( )
A. =±2 B. =5
C. ±2 D.
2. 的算术平方根是( )
A.2 B.±2
C. D.±
C
B
3.有下列说法:①一个数的立方根有两个,它们互为相反数;②若x3=(-2)3,则x=-2;③15的立方根是 ;④任何有理数都有立方根,它不是正数就是负数.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
4.若一个数的立方根与它本身相同,则这个数是( )
A.0 B.0或1 C.0或-1 D.0或±1
B
D
5. 若 是5的立方根,则b=____,若 =-2,则a=_______.
6. 分析下列四句话:
①因为(-3)3=-27,所以-3是-27的立方根;
②因为43=64,所以64是4的立方根;
③把2立方与把8开立方互为逆运算;
④把4立方与把4开平方互为逆运算.
其中正确的是_________.(填序号)
1
-8
①③
7.填一填:
(1)1的平方根是____;立方根为____;算术平方根为____.
(2)平方根是它本身的数是____.
(3)算术平方根是其本身的数是____.
(4) 的立方根为 .
(5) 的平方根为 .
(6) 的立方根为 .
1
1
±1
0
0, 1
±2
-2
-2
(1) (2) (3)
8. 计算:
8.求下列各式的值.
(1)
(2)
(3)
(4)
= – 0.3
=
=
=
=
=
10.求下列各式中x的值:
(1)x3=-
;
(2)4(x-1)3=-256.
解:(1)x= =- .
(2)(x-1)3=-64,x-1=-4,x=-3.
11.若 =2, =4,求 的值.
解:∵ =2, =4.
∴x = 23,y2 = 16,
∴x = 8,y = ±4.
∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
∴ = = 4 或 = = 0.
课堂小结
立方根
规律
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a 的三次方根.
性质
正数的立方根是正数,
负数的立方根是负数;
0的立方根是0 .
定义
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
