冀教版数学八年级上册同步课件:14.3.2 实数的分类 (共26张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:14.3.2 实数的分类 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 418.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 16:25:26 | ||
图片预览







文档简介
(共26张PPT)
第十四章 实数
14.3 实数
第2课时 实数的分类
知识回顾
1.什么叫做无理数?什么叫做实数?
无限不循环小数叫做无理数,有理数和无理数统称为实数.
绝对值相等,符号不同的两数叫做相反数,其中一个是另一个的相反数.
数轴上表示数a的点到原点的距离叫做数a的绝对值,用︱a︱表示.
如果两个数的积是1,则这两个数互为倒数 .
2.有理数中的几个重要概念:什么是相反数?什么是绝对值?什么是倒数?
思考:无理数也有相反数吗?怎么表示?有绝对值吗?怎么表示?有倒数吗?怎么表示?
情景导入
如图,图中每个小正方形的边长均为1,则图中阴影部分(正方形)的边长是多少?这是一个什么数?
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
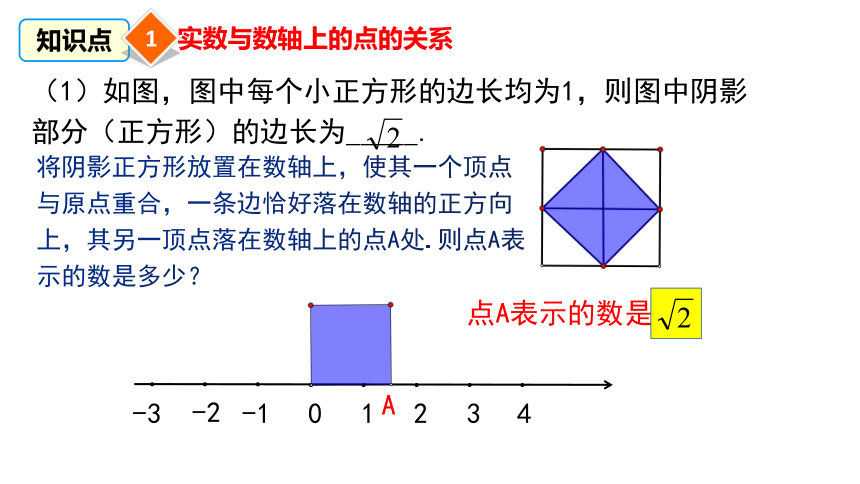
将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的正方向上,其另一顶点落在数轴上的点A处.则点A表示的数是多少?
A
(1)如图,图中每个小正方形的边长均为1,则图中阴影部分(正方形)的边长为_____.
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的正方向上,其另一顶点落在数轴上的点A处.则点A表示的数是多少?
A
点A表示的数是
知识点
实数与数轴上的点的关系
1
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
(2)若将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的负方向上,其另一顶点落在数轴上的点B处.则点B表示的数是多少?
B
点B表示的数是
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
(3)如图,设一枚5角硬币的直径为1个单位长度,将这枚硬币放置在一个数轴上,使硬币边缘上的一点P与原点重合.让这枚硬币沿数轴的正方向无滑动滚动一周.这时点P转到数轴上的点P处.则线段OP′的长是 ;点P′表示的数是 .
●
P(O)
P′
●
π
π
通过以上几个问题,你有什么发现?说说你的看法.
事实上,每个有理数或无理数都可以用数轴上的一个点来表示;反过来,数轴上的点表示的数是有理数或无理数.
实数与数轴间的关系:
实数和数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
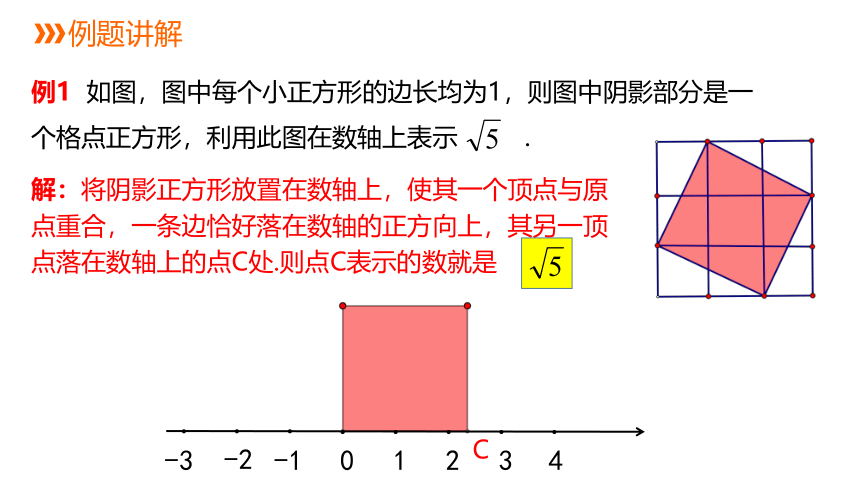
例1 如图,图中每个小正方形的边长均为1,则图中阴影部分是一个格点正方形,利用此图在数轴上表示 .
解:将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的正方向上,其另一顶点落在数轴上的点C处.则点C表示的数就是 .
C
例题讲解
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
变式练习1 如图,数轴上点A表示的数最可能是( )
A.﹣x B.﹣ C.﹣ D.﹣
C
绝对值
知识点
实数的性质
2
在有理数范围内的一些基本概念(如绝对值、相反数、倒数)在实数范围内依然适用.
一个正实数的绝对值是它本身.
一个负实数的绝对值是它的相反数.
0的绝对值是0.
即:|a|=
相反数
实数a的相反数为-a,若a,b互为相反数,则a+b=0.
0的相反数是0.
0没有倒数.
乘积为1的两个实数互为倒数.
倒数
非零实数a的倒数为 ,若a,b互为倒数,则ab=1.
例题讲解
例2 分别求下列各数的相反数、倒数和绝对值.
解:(1)∵ =-4,
∴ 的相反数是4,倒数是 ,绝对值是4.
(2) 的相反数是- ,倒数是 ,绝对值是 .
(3) 3.14-π的相反数是-(3.14-π),即π-3.14.
3.14-π的倒数是 .
∵3.14-π<0,∴|3.14-π|=-(3.14-π)=π-3.14.
变式练习2
知识点
实数的分类
3
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
或 有理数
整数
分数
(无限不循环小数)
(有限小数或无限循环小数)
按概念分类:
按正负性分类:
例3 把下列各数填入相应的集合内.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
注意:1.0既不是正数,也不是负数;
2.按从前往后的顺序找,做到不重不漏.
随堂演练
D
1.下列说法正确的是( )
A.正实数和负实数统称实数
B.正数、零和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
2.下列各组数中,互为相反数的是( )
A.-3与 B.|-3|与
C.|-3|与 D.-3与
D
3.2- 的绝对值是( )
A.2- B. -2
C.2+ D.±(2- )
B
4.下列说法正确的是__________.
①-a的绝对值是a;
②实数分为正实数和负实数;
③实数与数轴上的点具有一一对应的关系;
④实数a一定有倒数 ;
⑤π-1与1-π互为相反数;
③⑤
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
a
●
2-a
7.(1)求 的相反数和倒数;
(2)已知 = ,求a.
解:(1)因为 ,3的相反数是-3,所以 的相反数是-3,倒数是 .
(2)因为 , ,所以a的值是 和 .
8.把下列各数填到相应的位置.
正实数
负实数
.把下列各数填到相应的位置.
有理数
无理数
10.求下列各数的相反数、倒数和绝对值:
;
;
.
解:
对于题目:实数a,b,c的大小如图中数轴所示,化简:|a﹣c|﹣|a﹣b|+|c﹣b|+2c.
张皓程的解法如图所示:
(1)张皓程从第 步开始出错.
(2)请你写出正确的解答过程.
①
解:(1)因为c<0<a<b,且|b|>|a|>|c|,
所以a﹣c>0,a﹣b<0,c﹣b<0,
所以|a﹣c|﹣|a﹣b|+|c﹣b|+2c=(a﹣c)+(a﹣b)﹣(c﹣b)+2c
所以是第①步出错,原因是去绝对值符号时,负数没有变号;
故答案为:①;
(2)因为c<0<a<b,且|b|>|a|>|c|,
所以a﹣c>0,a﹣b<0,c﹣b<0,
|a﹣c|﹣|a﹣b|+|c﹣b|+2c
=(a﹣c)+(a﹣b)﹣(c﹣b)+2c
=a﹣c+a﹣b﹣c+b+2c
=2a.
课堂小结
实数
实数的分类
相反数
实数与数轴上的点的关系
实数的性质
倒数
按正负性分类
绝对值
按概念分类
一一对应
第十四章 实数
14.3 实数
第2课时 实数的分类
知识回顾
1.什么叫做无理数?什么叫做实数?
无限不循环小数叫做无理数,有理数和无理数统称为实数.
绝对值相等,符号不同的两数叫做相反数,其中一个是另一个的相反数.
数轴上表示数a的点到原点的距离叫做数a的绝对值,用︱a︱表示.
如果两个数的积是1,则这两个数互为倒数 .
2.有理数中的几个重要概念:什么是相反数?什么是绝对值?什么是倒数?
思考:无理数也有相反数吗?怎么表示?有绝对值吗?怎么表示?有倒数吗?怎么表示?
情景导入
如图,图中每个小正方形的边长均为1,则图中阴影部分(正方形)的边长是多少?这是一个什么数?
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的正方向上,其另一顶点落在数轴上的点A处.则点A表示的数是多少?
A
(1)如图,图中每个小正方形的边长均为1,则图中阴影部分(正方形)的边长为_____.
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的正方向上,其另一顶点落在数轴上的点A处.则点A表示的数是多少?
A
点A表示的数是
知识点
实数与数轴上的点的关系
1
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
(2)若将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的负方向上,其另一顶点落在数轴上的点B处.则点B表示的数是多少?
B
点B表示的数是
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
(3)如图,设一枚5角硬币的直径为1个单位长度,将这枚硬币放置在一个数轴上,使硬币边缘上的一点P与原点重合.让这枚硬币沿数轴的正方向无滑动滚动一周.这时点P转到数轴上的点P处.则线段OP′的长是 ;点P′表示的数是 .
●
P(O)
P′
●
π
π
通过以上几个问题,你有什么发现?说说你的看法.
事实上,每个有理数或无理数都可以用数轴上的一个点来表示;反过来,数轴上的点表示的数是有理数或无理数.
实数与数轴间的关系:
实数和数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
例1 如图,图中每个小正方形的边长均为1,则图中阴影部分是一个格点正方形,利用此图在数轴上表示 .
解:将阴影正方形放置在数轴上,使其一个顶点与原点重合,一条边恰好落在数轴的正方向上,其另一顶点落在数轴上的点C处.则点C表示的数就是 .
C
例题讲解
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
变式练习1 如图,数轴上点A表示的数最可能是( )
A.﹣x B.﹣ C.﹣ D.﹣
C
绝对值
知识点
实数的性质
2
在有理数范围内的一些基本概念(如绝对值、相反数、倒数)在实数范围内依然适用.
一个正实数的绝对值是它本身.
一个负实数的绝对值是它的相反数.
0的绝对值是0.
即:|a|=
相反数
实数a的相反数为-a,若a,b互为相反数,则a+b=0.
0的相反数是0.
0没有倒数.
乘积为1的两个实数互为倒数.
倒数
非零实数a的倒数为 ,若a,b互为倒数,则ab=1.
例题讲解
例2 分别求下列各数的相反数、倒数和绝对值.
解:(1)∵ =-4,
∴ 的相反数是4,倒数是 ,绝对值是4.
(2) 的相反数是- ,倒数是 ,绝对值是 .
(3) 3.14-π的相反数是-(3.14-π),即π-3.14.
3.14-π的倒数是 .
∵3.14-π<0,∴|3.14-π|=-(3.14-π)=π-3.14.
变式练习2
知识点
实数的分类
3
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
或 有理数
整数
分数
(无限不循环小数)
(有限小数或无限循环小数)
按概念分类:
按正负性分类:
例3 把下列各数填入相应的集合内.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
注意:1.0既不是正数,也不是负数;
2.按从前往后的顺序找,做到不重不漏.
随堂演练
D
1.下列说法正确的是( )
A.正实数和负实数统称实数
B.正数、零和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
2.下列各组数中,互为相反数的是( )
A.-3与 B.|-3|与
C.|-3|与 D.-3与
D
3.2- 的绝对值是( )
A.2- B. -2
C.2+ D.±(2- )
B
4.下列说法正确的是__________.
①-a的绝对值是a;
②实数分为正实数和负实数;
③实数与数轴上的点具有一一对应的关系;
④实数a一定有倒数 ;
⑤π-1与1-π互为相反数;
③⑤
●
●
●
●
●
●
●
3
2
1
0
-2
-1
4
●
-3
a
●
2-a
7.(1)求 的相反数和倒数;
(2)已知 = ,求a.
解:(1)因为 ,3的相反数是-3,所以 的相反数是-3,倒数是 .
(2)因为 , ,所以a的值是 和 .
8.把下列各数填到相应的位置.
正实数
负实数
.把下列各数填到相应的位置.
有理数
无理数
10.求下列各数的相反数、倒数和绝对值:
;
;
.
解:
对于题目:实数a,b,c的大小如图中数轴所示,化简:|a﹣c|﹣|a﹣b|+|c﹣b|+2c.
张皓程的解法如图所示:
(1)张皓程从第 步开始出错.
(2)请你写出正确的解答过程.
①
解:(1)因为c<0<a<b,且|b|>|a|>|c|,
所以a﹣c>0,a﹣b<0,c﹣b<0,
所以|a﹣c|﹣|a﹣b|+|c﹣b|+2c=(a﹣c)+(a﹣b)﹣(c﹣b)+2c
所以是第①步出错,原因是去绝对值符号时,负数没有变号;
故答案为:①;
(2)因为c<0<a<b,且|b|>|a|>|c|,
所以a﹣c>0,a﹣b<0,c﹣b<0,
|a﹣c|﹣|a﹣b|+|c﹣b|+2c
=(a﹣c)+(a﹣b)﹣(c﹣b)+2c
=a﹣c+a﹣b﹣c+b+2c
=2a.
课堂小结
实数
实数的分类
相反数
实数与数轴上的点的关系
实数的性质
倒数
按正负性分类
绝对值
按概念分类
一一对应
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
