冀教版数学八年级上册同步课件:14.4 近似数(共26张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:14.4 近似数(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 519.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 16:11:05 | ||
图片预览








文档简介
(共26张PPT)
第十四章 实数
14.4 近似数
知识回顾
2.你对实数怎么进行分类?快速画一画,然后跟同学分享一下吧.
1.什么叫做无理数?什么叫做实数?
无限不循环小数叫做无理数,有理数和无理数统称为实数.
情景导入
周末,舅妈一家4口人来小明家做客,小明的妈妈从超市买了2.4千克水果、1.8千克蔬菜、1.2千克大虾、2.1千克排骨……你知道这些数字怎么得到的吗?
实际生活中,有时候不可能得到准确值,有时候没必要得到准确值,这时往往取数据的近似值就可以了.
获取新知
知识点
近似数的定义
1
在进行实数的计算时,有时需要估计实数的范围或者按一定的精确度取近似的数,这就是我们将要学习的近似数.
我们知道
= 1. 414 213 562 373 095 048 801 688 724 209 698 078 569 …,
π=3. 141 592 653 589 793 238 462 643 383 279 502 884 197 ….
概念学习
在实际计算中,不可能(也没必要)将它们所有数位上的数字都写出来,往往取它的一个近似的数值即可.
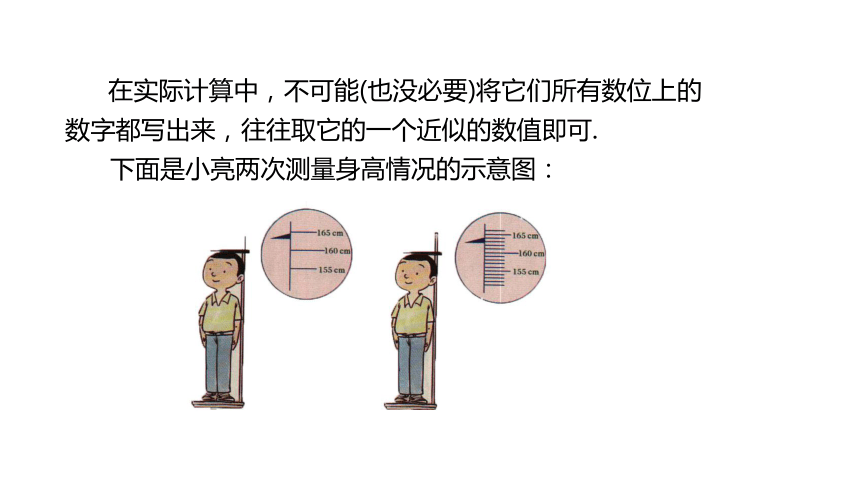
下面是小亮两次测量身高情况的示意图:
1. 根据上面左图读出的数据,小亮的身高是1.63 m;根据上面右图读出的数据,小亮的身高是1.628 m.这两个数据都是准确的吗?
2. 1.63中的三个数字,哪些数字是准确的,哪个数字不一定准确?对于1.628中的四个数字,哪些数字是准确的,哪个数字不一定准确?
通常,我们用1. 63 m来表示小亮的身高就足够了.
例如 ,根据计算要求,一般取1.4,1.414,…作为它的近似值.又如π,一般取它的近似值3, 3.14, 3.141 6,等等.
定义: 像这样,接近实际的数或在计算中按要求所取的与某个准确数接近的数,我们把它叫做近似数.
近似数产生的原因
①“计算”产生近似数,如除不尽,有圆周率π参与计算的结果;
②用测量工具测出的一般都是近似数,如长度、质量、时间等;
③不容易得到或不可能得到准确数,如人口普查的结果、星球的年龄,就只能是一个近似数.
在日常生活中,你遇到的近似数有哪些?谈一下吧......
例1 下列语句中,那些数据是精确的,哪些数据是近似的?
(1)我国的国土面积是960万平方千米.
(2)小民与小李买了 2 瓶水,4 根黄瓜,6 袋香巴拉牛肉干,花了 20 元,然后骑车去大约 3.5 km外去郊游,大约玩了 4.5 小时回家.
(3)检查一双没洗过的手,发现带有各种细菌约80 000万个.
解:精确数:2,4,6;
近似数:960,20,3.5,80000,4.5.
例题讲解
变式练习1
(课本80页“大家谈谈”)在下列问题中,哪些是准确数,哪些是近似数?
(1)妈妈花10元钱买了2kg香蕉.
(2)某教学楼共有5层,每层的楼梯都是28级台阶,经测量,每级台阶的高是12cm.从而教学楼的高度是5×28×0.12=16.8(m).
(3)小亮用直尺测量一本数学课本的厚度是1.05cm,由此,他认为10本这样的数学课本摞起来的高度就是10.5cm.
由测量产生的数据,一般都有误差,这些数都是近似数.
知识点
近似数的精确度
2
精准度
近似数与准确数的接近程度,其表述形式多样,如:精确到个位、精确到0.001、保留两位小数等.
一般地,一个近似数四舍五入到哪一位,就说这个数精确到哪一位.
确定方法:一个近似数的取值需要它精确到的位数的下一位,若下一位小于五,则“四舍”,得到的近似数比原数小.若下一位大于或等于五,则“五入”,得到的近似数比原数大.
例2 将圆周率π按下列要求取近似数:
(1)精确到个位; (2)精确到十分位.
解:(1) π的十分位(即小数点后面第一位)上是“1”,按四舍五入法应舍去,所以π=3.
(2)π的百分位(即小数点后面第二位)上是“4”,按四舍五入法应舍去,所以π≈3.1.
例题讲解
π≈3(精确到个位),
π≈3.1(精确到0.1,或叫做精确到十分位),
π≈3.14(精确到0.01,或叫精确到百分位),
π≈3.140(精确到0.001,或叫做精确到千分位 ),
π≈3.1416(精确到0.0001,或叫做精确到万分位),
……
按四舍五入法对圆周率π取近似数,有
变式练习2 用四舍五入法写出下列各数的近似数:
(1)4.357(精确到0.01);
(2)472 086(精确到万位);
(3)0.473 954(精确到千分位);
(4)5.328 06(保留两位小数).
解:(1)4.357≈4.36.
(2)472 086≈47万.
(3)0.473 954≈0.474.
(4)5.328 06≈5.33.
变式练习3 资阳市2012年财政收入取得重大突破,地方公共财政收入用四舍五入法取近 似值后为27.39亿元,那么这个数值( )
A.精确到亿位 B.精确到百分位
C.精确到千万位 D.精确到百万位
D
归纳
确定近似数的精确度就是确定近似数的末位数字所在的数.对于a×10n的精确度,应由还原后的数中数a的末位数字所在的数位决定;对于带单位的近似数(如:6万),精确度也是由还原后的数中近似数的末位数字所在的数位决定.
知识点
近似数的取值范围
3
例3 近似数1.70所表示的准确数x的取值范围是( )
A.1.695≤x<1.705 B.1.65≤x<1.75
C.1.7≤x<1.75 D.1.695≤x≤1.705
解析:近似数1.70精确到百分位,应由千分位上的数字四舍五入得到.故当百分位上为9时,千分位上的数应不小于5;当百分位上为0时,千分位上的数应小于5.
A
方法归纳
由近似数确定准确数的范围时,只需在近似数的最后一位之后再取一位,数值记为0,再在这一位上加减5即可.如a≈1.70,可取1.700,用1.700-0.005=1.695,1.700+0.005=1.705,同时注意“含小不含大”,即1.695≤a<1.705.
变式练习3 由四舍五入得到的近似数是3.75,那么原数不可能是( )
A.3.751 4 B.3.749 3
C.3.750 4 D.3.755
D
随堂演练
1.下列语句中出现的数,是近似数的是( )
A.小明同学买了6支铅笔 B.一星期有7天
C.一本书共有180页 D.小华的身高为1.6 m
2. 下列数据中,是准确数的是( )
A.小轩体重51.2 kg
B.七(3)班有64名学生
C.珠穆朗玛峰高出海平面8 844.43 m
D.太平洋最深处低于海平面11 034 m
D
B
4.下列说法正确的是 ( )
A.近似数0.010精确到百分位
B.近似数4.3万精确到千位
C.近似数2.8和2.80表示的意义相同
D.近似数43.0精确到个位
B
3.按括号内的要求用四舍五入法取近似数,正确的是( )
A.403.53≈403(精确到个位) B.1.604≈1.60(精确到十分位)
C.0.02984≈0.030(精确到0.001) D.0.0136≈0.014(精确到0.0001)
C
5.判断下列各数,哪些是近似数,哪些是准确数
⑴某歌星在体育馆举办音乐会,大约有一万二千人参加;( )
⑵检查一双没洗过的手,发现带有各种细菌800000万个; ( )
⑶张明家里养了5只鸡; ( )
⑷据统计,2017年全国初中在校生人数为4311.95万. ( )
近似数
近似数
近似数
准确数
6.如果实数a由四舍五入得到的近似数为38,那么a的取值范围是_____________.
37.5≤a<38.5
7.小红量得课桌长为1.036米,请按下列要求取这个数的近似数.
(1)四舍五入到百分位;
(2)四舍五入到十分位;
(3)四舍五入到个位.
1.04米
1.0米
1米
8.下列由四舍五入得到的近似数,各精确到哪一位?
(1) 600万 ; (2) 7.03万;
(3) 5.8亿 ; (4)3.30×105.
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
(1)2.605(精确到十分位)
(2)2.605(精确0.01)
(3)170.543(精确到个位)
(4)1602108(精确到千位)
2.605≈2.6
2.605≈2.61
170.543≈171
1602108≈160.2万
9.用四舍五入法写出下列各数的近似数.
解:
10.向月球发射无线电波,无线电波到月球并返回地面需要2.57s,已知无线电波每秒传播3×105km,求地球和月球之间的距离(结果精确到千位).
解:
答:地球和月球之间的距离约为
11.车工小王加工生产了两根轴,当他把轴交给质检员验收时,质检员说:“不合格,作废!”小王不服气地说:“图纸要求精确到2.60m,我的一根为2.56m,一根为2.62m,怎么不合格?”
你认为是小王加工的轴不合格,还是质检员故意刁难小王?
解:近似数2.60m的要求是精确到0.01m,所以轴的范围是2.595≤x<2.605.小王的两根轴2.56m、2.62m没有在轴要求的范围之内,因此小王加工的轴不合格.
小王误以为2.6m和2.60m的精确度相同.
课堂小结
实际生活中的数
近似数
准群数:一般可数
按要求取近似值(四舍五入)
精确度(最右边数所占的数位)
精确到个位、精确到0.001、保留两位小数等
第十四章 实数
14.4 近似数
知识回顾
2.你对实数怎么进行分类?快速画一画,然后跟同学分享一下吧.
1.什么叫做无理数?什么叫做实数?
无限不循环小数叫做无理数,有理数和无理数统称为实数.
情景导入
周末,舅妈一家4口人来小明家做客,小明的妈妈从超市买了2.4千克水果、1.8千克蔬菜、1.2千克大虾、2.1千克排骨……你知道这些数字怎么得到的吗?
实际生活中,有时候不可能得到准确值,有时候没必要得到准确值,这时往往取数据的近似值就可以了.
获取新知
知识点
近似数的定义
1
在进行实数的计算时,有时需要估计实数的范围或者按一定的精确度取近似的数,这就是我们将要学习的近似数.
我们知道
= 1. 414 213 562 373 095 048 801 688 724 209 698 078 569 …,
π=3. 141 592 653 589 793 238 462 643 383 279 502 884 197 ….
概念学习
在实际计算中,不可能(也没必要)将它们所有数位上的数字都写出来,往往取它的一个近似的数值即可.
下面是小亮两次测量身高情况的示意图:
1. 根据上面左图读出的数据,小亮的身高是1.63 m;根据上面右图读出的数据,小亮的身高是1.628 m.这两个数据都是准确的吗?
2. 1.63中的三个数字,哪些数字是准确的,哪个数字不一定准确?对于1.628中的四个数字,哪些数字是准确的,哪个数字不一定准确?
通常,我们用1. 63 m来表示小亮的身高就足够了.
例如 ,根据计算要求,一般取1.4,1.414,…作为它的近似值.又如π,一般取它的近似值3, 3.14, 3.141 6,等等.
定义: 像这样,接近实际的数或在计算中按要求所取的与某个准确数接近的数,我们把它叫做近似数.
近似数产生的原因
①“计算”产生近似数,如除不尽,有圆周率π参与计算的结果;
②用测量工具测出的一般都是近似数,如长度、质量、时间等;
③不容易得到或不可能得到准确数,如人口普查的结果、星球的年龄,就只能是一个近似数.
在日常生活中,你遇到的近似数有哪些?谈一下吧......
例1 下列语句中,那些数据是精确的,哪些数据是近似的?
(1)我国的国土面积是960万平方千米.
(2)小民与小李买了 2 瓶水,4 根黄瓜,6 袋香巴拉牛肉干,花了 20 元,然后骑车去大约 3.5 km外去郊游,大约玩了 4.5 小时回家.
(3)检查一双没洗过的手,发现带有各种细菌约80 000万个.
解:精确数:2,4,6;
近似数:960,20,3.5,80000,4.5.
例题讲解
变式练习1
(课本80页“大家谈谈”)在下列问题中,哪些是准确数,哪些是近似数?
(1)妈妈花10元钱买了2kg香蕉.
(2)某教学楼共有5层,每层的楼梯都是28级台阶,经测量,每级台阶的高是12cm.从而教学楼的高度是5×28×0.12=16.8(m).
(3)小亮用直尺测量一本数学课本的厚度是1.05cm,由此,他认为10本这样的数学课本摞起来的高度就是10.5cm.
由测量产生的数据,一般都有误差,这些数都是近似数.
知识点
近似数的精确度
2
精准度
近似数与准确数的接近程度,其表述形式多样,如:精确到个位、精确到0.001、保留两位小数等.
一般地,一个近似数四舍五入到哪一位,就说这个数精确到哪一位.
确定方法:一个近似数的取值需要它精确到的位数的下一位,若下一位小于五,则“四舍”,得到的近似数比原数小.若下一位大于或等于五,则“五入”,得到的近似数比原数大.
例2 将圆周率π按下列要求取近似数:
(1)精确到个位; (2)精确到十分位.
解:(1) π的十分位(即小数点后面第一位)上是“1”,按四舍五入法应舍去,所以π=3.
(2)π的百分位(即小数点后面第二位)上是“4”,按四舍五入法应舍去,所以π≈3.1.
例题讲解
π≈3(精确到个位),
π≈3.1(精确到0.1,或叫做精确到十分位),
π≈3.14(精确到0.01,或叫精确到百分位),
π≈3.140(精确到0.001,或叫做精确到千分位 ),
π≈3.1416(精确到0.0001,或叫做精确到万分位),
……
按四舍五入法对圆周率π取近似数,有
变式练习2 用四舍五入法写出下列各数的近似数:
(1)4.357(精确到0.01);
(2)472 086(精确到万位);
(3)0.473 954(精确到千分位);
(4)5.328 06(保留两位小数).
解:(1)4.357≈4.36.
(2)472 086≈47万.
(3)0.473 954≈0.474.
(4)5.328 06≈5.33.
变式练习3 资阳市2012年财政收入取得重大突破,地方公共财政收入用四舍五入法取近 似值后为27.39亿元,那么这个数值( )
A.精确到亿位 B.精确到百分位
C.精确到千万位 D.精确到百万位
D
归纳
确定近似数的精确度就是确定近似数的末位数字所在的数.对于a×10n的精确度,应由还原后的数中数a的末位数字所在的数位决定;对于带单位的近似数(如:6万),精确度也是由还原后的数中近似数的末位数字所在的数位决定.
知识点
近似数的取值范围
3
例3 近似数1.70所表示的准确数x的取值范围是( )
A.1.695≤x<1.705 B.1.65≤x<1.75
C.1.7≤x<1.75 D.1.695≤x≤1.705
解析:近似数1.70精确到百分位,应由千分位上的数字四舍五入得到.故当百分位上为9时,千分位上的数应不小于5;当百分位上为0时,千分位上的数应小于5.
A
方法归纳
由近似数确定准确数的范围时,只需在近似数的最后一位之后再取一位,数值记为0,再在这一位上加减5即可.如a≈1.70,可取1.700,用1.700-0.005=1.695,1.700+0.005=1.705,同时注意“含小不含大”,即1.695≤a<1.705.
变式练习3 由四舍五入得到的近似数是3.75,那么原数不可能是( )
A.3.751 4 B.3.749 3
C.3.750 4 D.3.755
D
随堂演练
1.下列语句中出现的数,是近似数的是( )
A.小明同学买了6支铅笔 B.一星期有7天
C.一本书共有180页 D.小华的身高为1.6 m
2. 下列数据中,是准确数的是( )
A.小轩体重51.2 kg
B.七(3)班有64名学生
C.珠穆朗玛峰高出海平面8 844.43 m
D.太平洋最深处低于海平面11 034 m
D
B
4.下列说法正确的是 ( )
A.近似数0.010精确到百分位
B.近似数4.3万精确到千位
C.近似数2.8和2.80表示的意义相同
D.近似数43.0精确到个位
B
3.按括号内的要求用四舍五入法取近似数,正确的是( )
A.403.53≈403(精确到个位) B.1.604≈1.60(精确到十分位)
C.0.02984≈0.030(精确到0.001) D.0.0136≈0.014(精确到0.0001)
C
5.判断下列各数,哪些是近似数,哪些是准确数
⑴某歌星在体育馆举办音乐会,大约有一万二千人参加;( )
⑵检查一双没洗过的手,发现带有各种细菌800000万个; ( )
⑶张明家里养了5只鸡; ( )
⑷据统计,2017年全国初中在校生人数为4311.95万. ( )
近似数
近似数
近似数
准确数
6.如果实数a由四舍五入得到的近似数为38,那么a的取值范围是_____________.
37.5≤a<38.5
7.小红量得课桌长为1.036米,请按下列要求取这个数的近似数.
(1)四舍五入到百分位;
(2)四舍五入到十分位;
(3)四舍五入到个位.
1.04米
1.0米
1米
8.下列由四舍五入得到的近似数,各精确到哪一位?
(1) 600万 ; (2) 7.03万;
(3) 5.8亿 ; (4)3.30×105.
解:(1)600万,精确到万位;
(2)7.03万,精确到百位;
(3)5.8亿,精确到千万位;
(4)3.30×105,精确到千位.
(1)2.605(精确到十分位)
(2)2.605(精确0.01)
(3)170.543(精确到个位)
(4)1602108(精确到千位)
2.605≈2.6
2.605≈2.61
170.543≈171
1602108≈160.2万
9.用四舍五入法写出下列各数的近似数.
解:
10.向月球发射无线电波,无线电波到月球并返回地面需要2.57s,已知无线电波每秒传播3×105km,求地球和月球之间的距离(结果精确到千位).
解:
答:地球和月球之间的距离约为
11.车工小王加工生产了两根轴,当他把轴交给质检员验收时,质检员说:“不合格,作废!”小王不服气地说:“图纸要求精确到2.60m,我的一根为2.56m,一根为2.62m,怎么不合格?”
你认为是小王加工的轴不合格,还是质检员故意刁难小王?
解:近似数2.60m的要求是精确到0.01m,所以轴的范围是2.595≤x<2.605.小王的两根轴2.56m、2.62m没有在轴要求的范围之内,因此小王加工的轴不合格.
小王误以为2.6m和2.60m的精确度相同.
课堂小结
实际生活中的数
近似数
准群数:一般可数
按要求取近似值(四舍五入)
精确度(最右边数所占的数位)
精确到个位、精确到0.001、保留两位小数等
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
