冀教版数学八年级上册同步课件:15.2 二次根式的乘除运算(共29张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:15.2 二次根式的乘除运算(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 771.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览








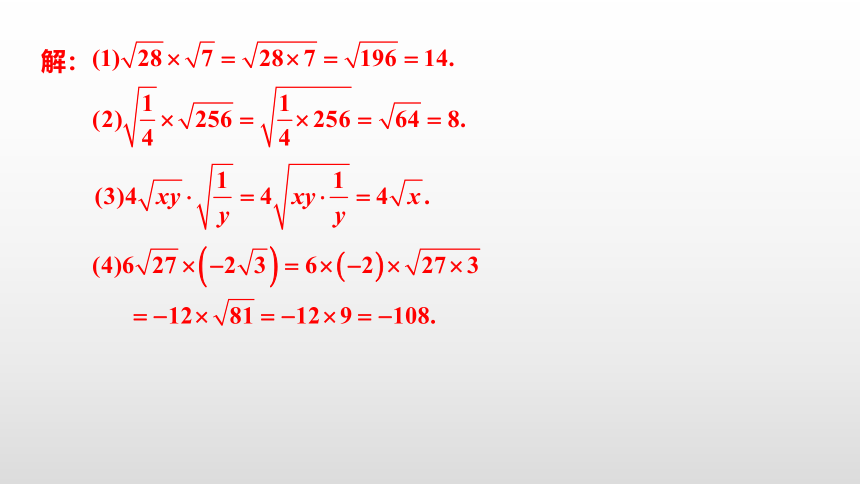
文档简介
(共29张PPT)
第十五章 二次根式
15.2 二次根式的乘除运算
知识回顾
我们学过二次根式的哪些性质?
情景导入
×
学校教学楼前有一矩形花坛(长宽如图所示),现在学校根据需要,要把它改建为草坪.若全部铺满,请同学们预算一下:需购买多少平方米的草皮呢?
获取新知
知识点
二次根式的乘法
1
(1) =_______, =_______;
(2) =_______, =_______;
(3) =_______, =_______.
6
6
20
20
30
30
做一做 计算下列各式, 观察计算结果,试着归纳其中规律.
发现
归纳
注意:(1)a≥0,b≥0是公式成立的必要条件;
(2)公式中的a、b既可以是数,也可以是代数式,但都必须是非负的;
(3)此法则也可以推广为
二次根式的乘法法则:两个二次根式相乘,将它们的被开方数相乘.
注意:二次根式的乘法与积的算术平方根是互逆运算关系.
例1 计算下列各式:
解:
例题讲解
1. 两个二次根式相乘,被开方数的积能开方的一定要开方;
2. 当二次根式根号外有因数(式)时,可类比单项式乘单项式的法则进行运算,如 (b≥0,d≥0),即将根号外的因数(式)与根号外的因数(式)相乘的积作为积的系数,被开方数与被开方数相乘的积作为积的被开方数.
温馨提示:
变式练习1 计算:
解析:(1)(2)两题直接利用公式 (a≥0,b≥0)计算;(3)(4)两题要利用乘法交换律和结合律,将二次根式根号外的因数(式)和两个二次根式分别相乘,同时注意确定积的符号.
解:
(a≥0,b≥0)
根号外的系数与系数相乘,积为结果的系数.
根式和根式按公式相乘.
图解
知识点
二次根式的除法
2
做一做 下列各式,观察计算结果,你能发现什么规律?
发现:
=
_______;
_______;
(2)
_______;
_______;
(3)
_______.
_______;
=
=
(a≥0,b>0).
归纳
二次根式的除法法则:二次根式相除,把被开方数相除,根指数不变.
例2 下列各式:
解:
温馨提示:利用二次根式的除法法则进行计算,被开方数相除时,可以用“除以一个不为零的数等于乘这个数的倒数”进行约分、化简.
变式练习2 计算:
(a>1,b>0).
解析:(1)直接利用二次根式的除法法则进行计算;(2)(4)要注意根号外的因数与因数相除,同时要注意结果的符号;(3)进行计算时需先把带分数化成假分数.
解:
在本例的解答过程中,将 分别化成了也就是将分母中含二次根式的式子化为 分母中不含二次根式的式子. 像这样,把分母中的二次根式化去,叫做分母有理化.
温馨提示:要想将分母有理化,其实质是将分子、分母同乘一个适当的数(式),
使分母转化为 的形式.
知识点
分母有理化
3
概念学习
例3 去掉下列各式分母中的二次根式:
(2)有多种方法:可以先运用二次根式的除法法则,再把被开方数进行化简,最后进行开方运算,也可以先分别把分子、分母进行化简,再将分子、分母同乘一个适当的数(式),化去分母中的根式;
(3)分子、分母同乘 .
解析:(1)分子、分母同乘
解:
分母有理化的一般步骤:
“一移”,即将分子、分母中能开得尽方的因数(式)开方后移到根号外;
“ 二乘”,即将分子、分母同乘分母的有理化因数(式);
“ 三化”,即化简计算.
归纳
变式练习3 如果a= +2,b= ,则( )
A.a>b B.a=b C.a<b D.a=
B
解析:直接将b分母有理化,∵b= = = +2,∴a=b.
小明的做法(先运算后化简)
解:
大刚的做法(先化简后运算)
解:
请就小明和大刚分别计算
的做法给予评价,并谈谈你的想法.
大家谈谈
解:
变式练习4 将下列各式中的根号化去:
随堂演练
1.计算 的结果是( )
A. B.4 C. D.2
B
2.计算 的结果是( )
A. B. C. D.
C
3.化简 的结果是( )
A. B. C. D.
D
4.下列计算正确的是( )
D
5.将下列各式分母中的二次根式去掉:
(1) (2)
(3) (4)
解:
6.计算下列各式.
多个二次根式乘除的
一般步骤:
1.确定符号;
2.根号内外分别作计算;
3.化简结果.
课堂小结
二次根式的乘除运算
分母有理化
二次根式的乘法
“ 二乘”,即将分子、分母同乘分母的有理化因数(式)
二次根式的除法
“ 三化”,即化简计算.
“一移”,即将分子、分母中能开得尽方的因数(式)开方后移到根号外
(a≥0,b>0)
第十五章 二次根式
15.2 二次根式的乘除运算
知识回顾
我们学过二次根式的哪些性质?
情景导入
×
学校教学楼前有一矩形花坛(长宽如图所示),现在学校根据需要,要把它改建为草坪.若全部铺满,请同学们预算一下:需购买多少平方米的草皮呢?
获取新知
知识点
二次根式的乘法
1
(1) =_______, =_______;
(2) =_______, =_______;
(3) =_______, =_______.
6
6
20
20
30
30
做一做 计算下列各式, 观察计算结果,试着归纳其中规律.
发现
归纳
注意:(1)a≥0,b≥0是公式成立的必要条件;
(2)公式中的a、b既可以是数,也可以是代数式,但都必须是非负的;
(3)此法则也可以推广为
二次根式的乘法法则:两个二次根式相乘,将它们的被开方数相乘.
注意:二次根式的乘法与积的算术平方根是互逆运算关系.
例1 计算下列各式:
解:
例题讲解
1. 两个二次根式相乘,被开方数的积能开方的一定要开方;
2. 当二次根式根号外有因数(式)时,可类比单项式乘单项式的法则进行运算,如 (b≥0,d≥0),即将根号外的因数(式)与根号外的因数(式)相乘的积作为积的系数,被开方数与被开方数相乘的积作为积的被开方数.
温馨提示:
变式练习1 计算:
解析:(1)(2)两题直接利用公式 (a≥0,b≥0)计算;(3)(4)两题要利用乘法交换律和结合律,将二次根式根号外的因数(式)和两个二次根式分别相乘,同时注意确定积的符号.
解:
(a≥0,b≥0)
根号外的系数与系数相乘,积为结果的系数.
根式和根式按公式相乘.
图解
知识点
二次根式的除法
2
做一做 下列各式,观察计算结果,你能发现什么规律?
发现:
=
_______;
_______;
(2)
_______;
_______;
(3)
_______.
_______;
=
=
(a≥0,b>0).
归纳
二次根式的除法法则:二次根式相除,把被开方数相除,根指数不变.
例2 下列各式:
解:
温馨提示:利用二次根式的除法法则进行计算,被开方数相除时,可以用“除以一个不为零的数等于乘这个数的倒数”进行约分、化简.
变式练习2 计算:
(a>1,b>0).
解析:(1)直接利用二次根式的除法法则进行计算;(2)(4)要注意根号外的因数与因数相除,同时要注意结果的符号;(3)进行计算时需先把带分数化成假分数.
解:
在本例的解答过程中,将 分别化成了也就是将分母中含二次根式的式子化为 分母中不含二次根式的式子. 像这样,把分母中的二次根式化去,叫做分母有理化.
温馨提示:要想将分母有理化,其实质是将分子、分母同乘一个适当的数(式),
使分母转化为 的形式.
知识点
分母有理化
3
概念学习
例3 去掉下列各式分母中的二次根式:
(2)有多种方法:可以先运用二次根式的除法法则,再把被开方数进行化简,最后进行开方运算,也可以先分别把分子、分母进行化简,再将分子、分母同乘一个适当的数(式),化去分母中的根式;
(3)分子、分母同乘 .
解析:(1)分子、分母同乘
解:
分母有理化的一般步骤:
“一移”,即将分子、分母中能开得尽方的因数(式)开方后移到根号外;
“ 二乘”,即将分子、分母同乘分母的有理化因数(式);
“ 三化”,即化简计算.
归纳
变式练习3 如果a= +2,b= ,则( )
A.a>b B.a=b C.a<b D.a=
B
解析:直接将b分母有理化,∵b= = = +2,∴a=b.
小明的做法(先运算后化简)
解:
大刚的做法(先化简后运算)
解:
请就小明和大刚分别计算
的做法给予评价,并谈谈你的想法.
大家谈谈
解:
变式练习4 将下列各式中的根号化去:
随堂演练
1.计算 的结果是( )
A. B.4 C. D.2
B
2.计算 的结果是( )
A. B. C. D.
C
3.化简 的结果是( )
A. B. C. D.
D
4.下列计算正确的是( )
D
5.将下列各式分母中的二次根式去掉:
(1) (2)
(3) (4)
解:
6.计算下列各式.
多个二次根式乘除的
一般步骤:
1.确定符号;
2.根号内外分别作计算;
3.化简结果.
课堂小结
二次根式的乘除运算
分母有理化
二次根式的乘法
“ 二乘”,即将分子、分母同乘分母的有理化因数(式)
二次根式的除法
“ 三化”,即化简计算.
“一移”,即将分子、分母中能开得尽方的因数(式)开方后移到根号外
(a≥0,b>0)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
