冀教版数学八年级上册同步课件:15.3 二次根式的加减运算(共22张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:15.3 二次根式的加减运算(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 413.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 16:18:25 | ||
图片预览







文档简介
(共22张PPT)
第十五章 二次根式
15.3 二次根式的加减运算
知识回顾
1.实数的加减运算法则是什么?
2.合并同类项的实质是什么?
乘法分配律的逆向运用.
加法法则:(1)同号两数相加,取相同的符号,并把它们的绝对值相加;(2)异号两数相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值.
减法法则:减去一个数等于加上这个数的相反数.
3.最简二次根式的两个条件是什么?
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式.
情景导入
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
思考:能截出两块正方形木板的条件是什么?
能用数学式子表示这个条件么
7.5dm
5dm
现在把问题转化为 是否成立,因此要计算
获取新知
知识点
被开方数相同的最简二次根式
1
下列3组二次根式,各有什么共同特征
要把它化成们最简二次根式再比较哦!
(1)二次根式的被开方数相同,都是
(2)二次根式的被开方数相同,都是
(3)化简后二次根式的被开方数相同,都是
可合并的二次根式的条件:
(1)最简二次根式;(2)被开方数相同.
详解:
(1)可合并的二次根式必须同时满足:最简二次根式和被开方数相同这两个条件;它与根号前面的数字因数无关;
(2)“可合并的二次根式”在习惯上及相关课外读物上都称为“同类二次根式”.
归纳
解析:化简各选项,得 , , , , 可以看出与 被开方数相同的选项是B.
例1 下列二次根式与 可以合并的是 ( )
A. B. C. D.
B
例题讲解
总结:解决本题的关键就是“一化二比”,“化”就是将二次根式化为最简二次根式,“比”就是比较化简后的被开方数.
变式练习1 如果最简二次根式 可以合并,求a、b的值.
解:∵最简二次根式 可以合并,
∴
知识点
二次根式的加减运算
2
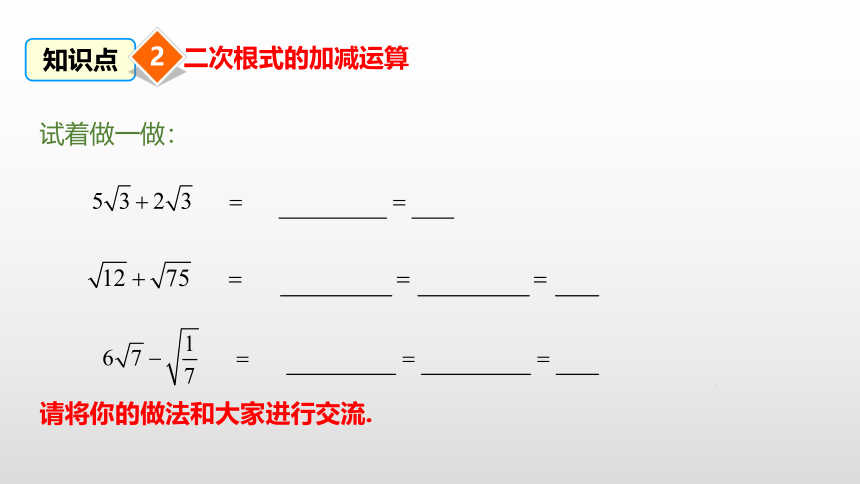
试着做一做:
请将你的做法和大家进行交流.
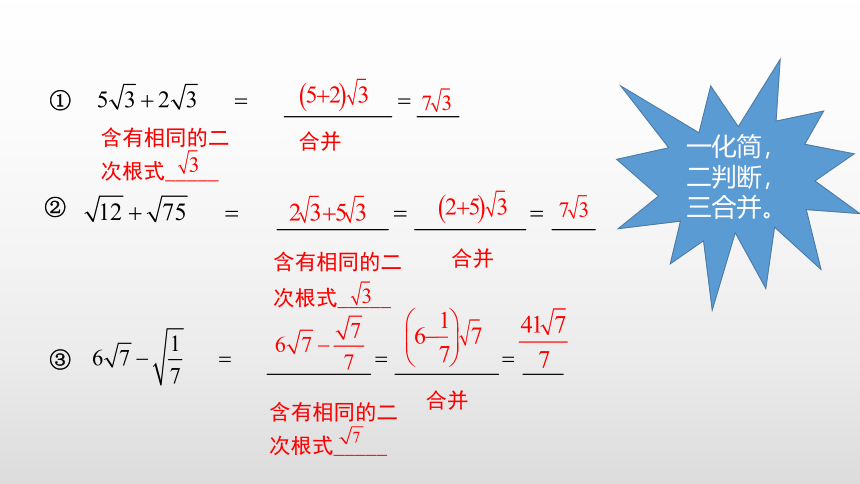
①
②
③
含有相同的二
次根式_____
合并
含有相同的二
次根式_____
含有相同的二
次根式_____
合并
合并
一化简,二判断,三合并。
归纳
二次根式的加减法
二次根式的加减运算,其实是将被开方数相同的项进行合并.为此,首先应将每个二次根式化简为最简二次根式,然后将被开方数相同的最简二次根式进行合并.
判定下列计算是否正确?
(1)
(4)
(3)
(2)
(1)(2)错误,
(3)(4)正确.
火眼金睛
例题讲解
例2 下计算列各式:
解:
1.合并结果中容易漏掉二次根式部分;
2.合并后根号外的因数是分数的要
写成假分数形式,不能写成带分数形式.
变式练习2 计算 的结果是( )
A. 4 B.
C. D.
D
例3 计算下列各式:
解:
温馨提示:运算顺序和运算律同于整式的运算
二次根式的加减法运算的步骤:
(1)将每个二次根式都化为最简二次根式,若被开方数
中含有带分数,则要先化成假分数;若含有小数,
则要化成分数,进而化为最简二次根式;
(2)原式中若有括号,要先去括号,再应用加法交换律、
结合律将被开方数相同的最简二次根式进行合并.
归纳
变式练习3 计算下列各式:
解:
随堂演练
2. 计算 的结果是( )
A. B. C. D.6
A
3.已知最简二次根式 与 能合并成一项,则x的值为( )
A.5 B.2 C.3 D.4
C
1.二次根式: 中,与 能进行合并的是 ( )
A.
B .
C .
D .
C
4.已知等腰三角形的两边长分别为 和 ,则这个等腰三角形的周长为( )
A. B.
C. D. 或
B
5.计算:
6.计算:
解:
解:
课堂小结
法则
2.找:找出被开方数相同的二次根式
二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.即:
步骤
3.合:类比合并同类项,将被开方数相同的二次根式合并
1.化:将二次根式化成最简二次根式
二次根式加减运算
第十五章 二次根式
15.3 二次根式的加减运算
知识回顾
1.实数的加减运算法则是什么?
2.合并同类项的实质是什么?
乘法分配律的逆向运用.
加法法则:(1)同号两数相加,取相同的符号,并把它们的绝对值相加;(2)异号两数相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值.
减法法则:减去一个数等于加上这个数的相反数.
3.最简二次根式的两个条件是什么?
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式.
情景导入
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
思考:能截出两块正方形木板的条件是什么?
能用数学式子表示这个条件么
7.5dm
5dm
现在把问题转化为 是否成立,因此要计算
获取新知
知识点
被开方数相同的最简二次根式
1
下列3组二次根式,各有什么共同特征
要把它化成们最简二次根式再比较哦!
(1)二次根式的被开方数相同,都是
(2)二次根式的被开方数相同,都是
(3)化简后二次根式的被开方数相同,都是
可合并的二次根式的条件:
(1)最简二次根式;(2)被开方数相同.
详解:
(1)可合并的二次根式必须同时满足:最简二次根式和被开方数相同这两个条件;它与根号前面的数字因数无关;
(2)“可合并的二次根式”在习惯上及相关课外读物上都称为“同类二次根式”.
归纳
解析:化简各选项,得 , , , , 可以看出与 被开方数相同的选项是B.
例1 下列二次根式与 可以合并的是 ( )
A. B. C. D.
B
例题讲解
总结:解决本题的关键就是“一化二比”,“化”就是将二次根式化为最简二次根式,“比”就是比较化简后的被开方数.
变式练习1 如果最简二次根式 可以合并,求a、b的值.
解:∵最简二次根式 可以合并,
∴
知识点
二次根式的加减运算
2
试着做一做:
请将你的做法和大家进行交流.
①
②
③
含有相同的二
次根式_____
合并
含有相同的二
次根式_____
含有相同的二
次根式_____
合并
合并
一化简,二判断,三合并。
归纳
二次根式的加减法
二次根式的加减运算,其实是将被开方数相同的项进行合并.为此,首先应将每个二次根式化简为最简二次根式,然后将被开方数相同的最简二次根式进行合并.
判定下列计算是否正确?
(1)
(4)
(3)
(2)
(1)(2)错误,
(3)(4)正确.
火眼金睛
例题讲解
例2 下计算列各式:
解:
1.合并结果中容易漏掉二次根式部分;
2.合并后根号外的因数是分数的要
写成假分数形式,不能写成带分数形式.
变式练习2 计算 的结果是( )
A. 4 B.
C. D.
D
例3 计算下列各式:
解:
温馨提示:运算顺序和运算律同于整式的运算
二次根式的加减法运算的步骤:
(1)将每个二次根式都化为最简二次根式,若被开方数
中含有带分数,则要先化成假分数;若含有小数,
则要化成分数,进而化为最简二次根式;
(2)原式中若有括号,要先去括号,再应用加法交换律、
结合律将被开方数相同的最简二次根式进行合并.
归纳
变式练习3 计算下列各式:
解:
随堂演练
2. 计算 的结果是( )
A. B. C. D.6
A
3.已知最简二次根式 与 能合并成一项,则x的值为( )
A.5 B.2 C.3 D.4
C
1.二次根式: 中,与 能进行合并的是 ( )
A.
B .
C .
D .
C
4.已知等腰三角形的两边长分别为 和 ,则这个等腰三角形的周长为( )
A. B.
C. D. 或
B
5.计算:
6.计算:
解:
解:
课堂小结
法则
2.找:找出被开方数相同的二次根式
二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.即:
步骤
3.合:类比合并同类项,将被开方数相同的二次根式合并
1.化:将二次根式化成最简二次根式
二次根式加减运算
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
