冀教版数学八年级上册同步课件:16.2.2 线段垂直平分线性质定理的逆定理(共25张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:16.2.2 线段垂直平分线性质定理的逆定理(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 209.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 16:24:14 | ||
图片预览






文档简介
(共25张PPT)
第十六章 轴对称和中心对称
16.2 线段垂直平分线
第2课时 线段垂直平分线性质定理的逆定理
知识回顾
什么叫做线段的垂直平分线?线段垂直平分线的性质定理内容是什么?
垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
线段垂直平分线上的点到线段两端点的距离相等.
几何语言:∵直线l垂直平分AB,点P在直线l上,
∴PA=PB.
A
B
P
C
l
情景导入
动手操作:在练习本上以线段AB为底边做等腰△PAB.
不确定
可以作无数个
△PAB的形状和大小是确定的吗?
符合条件的△PAB能作几个?
观察:你所画出的所有点P的位置,有什么特征?
在一条直线上
推测:这条直线与线段AB的关系
这条直线是线段AB的中垂线
A
B
P
思考:当PA=PB时,点P一定在AB的中垂线上吗?
折一折
获取新知
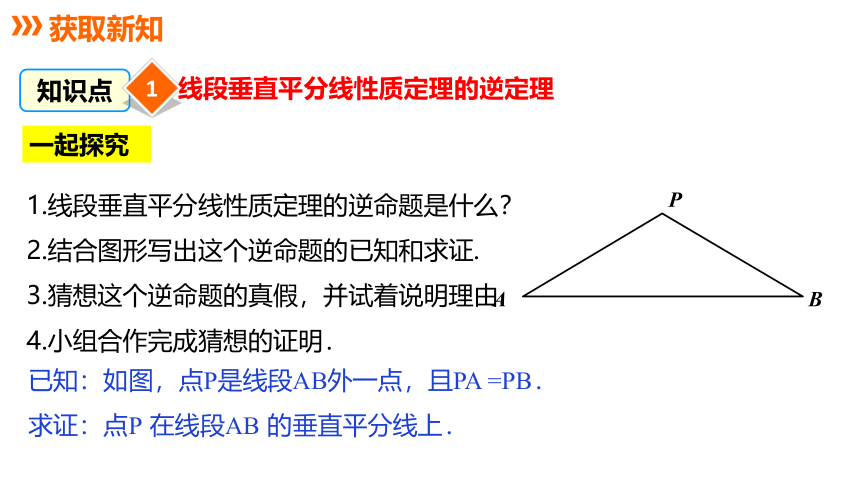
知识点
线段垂直平分线性质定理的逆定理
1
P
A
B
已知:如图,点P是线段AB外一点,且PA =PB.
求证:点P 在线段AB 的垂直平分线上.
一起探究
1.线段垂直平分线性质定理的逆命题是什么?
2.结合图形写出这个逆命题的已知和求证.
3.猜想这个逆命题的真假,并试着说明理由.
4.小组合作完成猜想的证明.
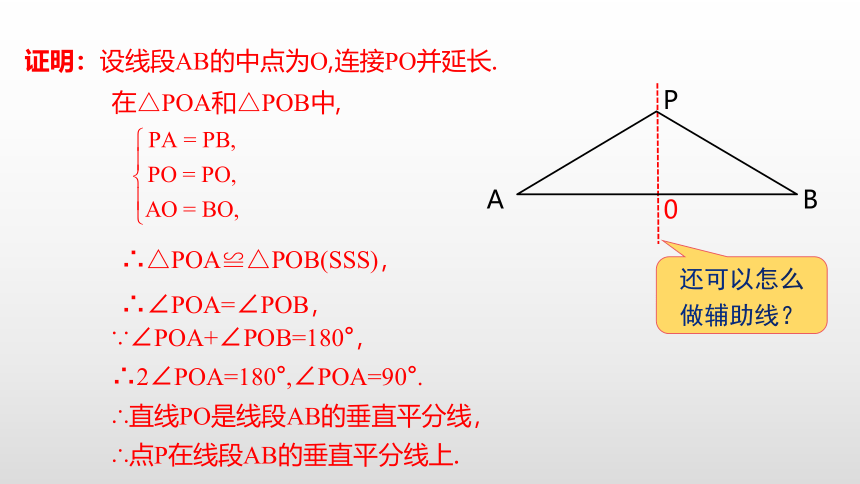
证明:设线段AB的中点为O,连接PO并延长.
在△POA和△POB中,
∴△POA≌△POB(SSS),
∴∠POA=∠POB,
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴直线PO是线段AB的垂直平分线,
∴点P在线段AB的垂直平分线上.
P
A
B
0
还可以怎么做辅助线?
证明:作∠APB的角平分线PO,交PO于点O.
在△POA 和△POB 中,
PA=PB,∠APO =∠BPO, PO =PO,
∴ △POA ≌△POB(SAS).
∴ ∠POA=∠POB
P
A
B
O
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴直线PO是线段AB的垂直平分线,
∴点P在线段AB的垂直平分线上.
证明:过点P 作AB 的垂线PO,垂足为点O.
则∠POA =∠POB =90°.
在Rt△P0A 和Rt△P0B 中,
PA =PB,PO=PO,
∴ Rt△POA ≌Rt△POB(HL).
∴ AO=BO.
又 PO⊥AB,
∴点P 在线段AB 的垂直平分线上.
P
A
B
O
这个方法下一章将要学.
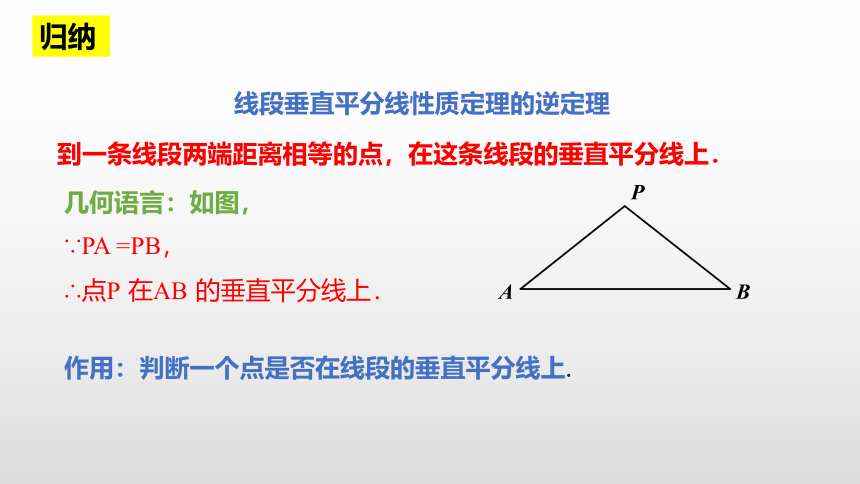
到一条线段两端距离相等的点,在这条线段的垂直平分线上.
几何语言:如图,
∵PA =PB,
∴点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
归纳
线段垂直平分线性质定理的逆定理
(2)若PA=PB,同时MA=MB,则直线PM是线段AB的中垂线吗?
P
A
B
l
不一定是.
理由:经过一点的直线有无数条.
思考:
(1)若PA=PB,过点P作直线l,则l是线段AB的中垂线吗?
是.
理由:两点确定一条直线.
M
归纳
几何语言:如图,
∵AB =AC,MB =MC,
∴点A、M均在线段BC的中垂线上
∴AM垂直平分BC
A
B
C
D
M
用线段垂直平分性质定理的逆定理判定线段垂直平分线的条件:必须有两个点到这条线段的两端距离相等.
判定线段垂直平分线的方法
1.用线段垂直平分线的定义.
2.用线段垂直平分线性质定理的逆定理,推出两个点都在线段的线段垂直平分线上,则过这两个点的直线就是这条线段的线段垂直平分线.
总结
例1 如图,在△ABC中,∠ACB=90°,AD平分 ∠BAC,DE⊥AB于E.
求证:直线AD是CE的垂直平分线.
分析:根据全等证CD=DE,所以点D 在CE的垂直平分线上,只要再证点A也在CE的垂直平分线上,就能解决问题.
证有两点在线段的垂直平分线上哦!
例题讲解
证明:∵AD平分∠BAC,
∴∠DAC=∠DAE,
∵DE⊥AB,
∴∠AED=∠ACB=90°,
在△ADC和△ADE中,
∠DAC=∠DAE,∠AED=∠ACB,AD=AD,
∴△ADC≌△ADE,
∴AC=AE,CD=ED,
∴点A、点D在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.
变式练习1 如图,四边形ABCD是一个“风筝”骨架,其中AB=AD,CB=CD.
C
B
A
D
E
(1)小明认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=EB,你同意他的说法吗?
解:同意,理由
∵AB=AD,CB=CD,
∴AC是BD的垂直平分线,
∴AC⊥BD,BE=EB.
C
B
A
D
E
(2)设对角线AC=a,BD=b,请用含a,b的式子表示四边形ABCD的面积.
知识点
线段垂直平分线性质定理和逆定理的综合运用
2
例2 已知:如图,△ABC的边AB、AC的垂直平分线相交于点P
求证:点P在BC的垂直平分线上
(1)由已知条件想到哪个定理?
线段垂直平分线的性质定理
(2)由结论想到哪个定理?
线段垂直平分线的性质的逆定理
A
B
P
C
D
E
证明:连接PA、PB、PC.
∵ 点P在AB、AC的垂直平分线上(已知)
∴ PA=PB,PA=PC
(线段垂直平分线上的点与线段两端距离相等)
∴ PB=PC(等量代换)
∴ 点P在BC的垂直平分线上(与线段两端距离相等的点在这条线段的垂直平分线上)
你发现了什么结论?
三角形的三边的中垂线相交于一点,这点到三角形三个顶点的距离相等.
归纳
A
B
P
C
D
E
变式练习2 如图,A,B,C表示三个居民小区,为丰富居民的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在( )
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边中垂线的交点处
D.∠A,∠B两内角平分线的交点处
C
B
A
C
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
A
2.已知线段AB,在平面上找到三个点D、E、F,使DA=DB,EA=EB,FA=FB,这样的点的组合共有( )种.
D
A.1 B.2 C.3 D.无数
随堂演练
3.如图,点D在△ABC的边BC上,且BC=BD+DA,则点D在线段( )的垂直平分线上.
A.AB
B.AC
C.BC
D.不能确定
B
D
C
B
A
4.下列说法:
①若点P、E是线段AB的垂直平分线上两点,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则经过点E的直线垂直平分线段AB.
其中正确的有 (填序号).
① ② ③
6.已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,∴∠DOE=∠COE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴△OED≌△OEC(AAS).
∴DO=CO,DE=CE.
∵EC⊥OA,ED⊥OB,∴∠EDO=∠ECO=90°.
课堂小结
线段的垂直平分的性质定理的逆定理
作用
内容
判断一个点是否在线段的垂直平分线上
到线段的两个端点距离相等的点在线段的垂直平分线上
第十六章 轴对称和中心对称
16.2 线段垂直平分线
第2课时 线段垂直平分线性质定理的逆定理
知识回顾
什么叫做线段的垂直平分线?线段垂直平分线的性质定理内容是什么?
垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
线段垂直平分线上的点到线段两端点的距离相等.
几何语言:∵直线l垂直平分AB,点P在直线l上,
∴PA=PB.
A
B
P
C
l
情景导入
动手操作:在练习本上以线段AB为底边做等腰△PAB.
不确定
可以作无数个
△PAB的形状和大小是确定的吗?
符合条件的△PAB能作几个?
观察:你所画出的所有点P的位置,有什么特征?
在一条直线上
推测:这条直线与线段AB的关系
这条直线是线段AB的中垂线
A
B
P
思考:当PA=PB时,点P一定在AB的中垂线上吗?
折一折
获取新知
知识点
线段垂直平分线性质定理的逆定理
1
P
A
B
已知:如图,点P是线段AB外一点,且PA =PB.
求证:点P 在线段AB 的垂直平分线上.
一起探究
1.线段垂直平分线性质定理的逆命题是什么?
2.结合图形写出这个逆命题的已知和求证.
3.猜想这个逆命题的真假,并试着说明理由.
4.小组合作完成猜想的证明.
证明:设线段AB的中点为O,连接PO并延长.
在△POA和△POB中,
∴△POA≌△POB(SSS),
∴∠POA=∠POB,
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴直线PO是线段AB的垂直平分线,
∴点P在线段AB的垂直平分线上.
P
A
B
0
还可以怎么做辅助线?
证明:作∠APB的角平分线PO,交PO于点O.
在△POA 和△POB 中,
PA=PB,∠APO =∠BPO, PO =PO,
∴ △POA ≌△POB(SAS).
∴ ∠POA=∠POB
P
A
B
O
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴直线PO是线段AB的垂直平分线,
∴点P在线段AB的垂直平分线上.
证明:过点P 作AB 的垂线PO,垂足为点O.
则∠POA =∠POB =90°.
在Rt△P0A 和Rt△P0B 中,
PA =PB,PO=PO,
∴ Rt△POA ≌Rt△POB(HL).
∴ AO=BO.
又 PO⊥AB,
∴点P 在线段AB 的垂直平分线上.
P
A
B
O
这个方法下一章将要学.
到一条线段两端距离相等的点,在这条线段的垂直平分线上.
几何语言:如图,
∵PA =PB,
∴点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
归纳
线段垂直平分线性质定理的逆定理
(2)若PA=PB,同时MA=MB,则直线PM是线段AB的中垂线吗?
P
A
B
l
不一定是.
理由:经过一点的直线有无数条.
思考:
(1)若PA=PB,过点P作直线l,则l是线段AB的中垂线吗?
是.
理由:两点确定一条直线.
M
归纳
几何语言:如图,
∵AB =AC,MB =MC,
∴点A、M均在线段BC的中垂线上
∴AM垂直平分BC
A
B
C
D
M
用线段垂直平分性质定理的逆定理判定线段垂直平分线的条件:必须有两个点到这条线段的两端距离相等.
判定线段垂直平分线的方法
1.用线段垂直平分线的定义.
2.用线段垂直平分线性质定理的逆定理,推出两个点都在线段的线段垂直平分线上,则过这两个点的直线就是这条线段的线段垂直平分线.
总结
例1 如图,在△ABC中,∠ACB=90°,AD平分 ∠BAC,DE⊥AB于E.
求证:直线AD是CE的垂直平分线.
分析:根据全等证CD=DE,所以点D 在CE的垂直平分线上,只要再证点A也在CE的垂直平分线上,就能解决问题.
证有两点在线段的垂直平分线上哦!
例题讲解
证明:∵AD平分∠BAC,
∴∠DAC=∠DAE,
∵DE⊥AB,
∴∠AED=∠ACB=90°,
在△ADC和△ADE中,
∠DAC=∠DAE,∠AED=∠ACB,AD=AD,
∴△ADC≌△ADE,
∴AC=AE,CD=ED,
∴点A、点D在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.
变式练习1 如图,四边形ABCD是一个“风筝”骨架,其中AB=AD,CB=CD.
C
B
A
D
E
(1)小明认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=EB,你同意他的说法吗?
解:同意,理由
∵AB=AD,CB=CD,
∴AC是BD的垂直平分线,
∴AC⊥BD,BE=EB.
C
B
A
D
E
(2)设对角线AC=a,BD=b,请用含a,b的式子表示四边形ABCD的面积.
知识点
线段垂直平分线性质定理和逆定理的综合运用
2
例2 已知:如图,△ABC的边AB、AC的垂直平分线相交于点P
求证:点P在BC的垂直平分线上
(1)由已知条件想到哪个定理?
线段垂直平分线的性质定理
(2)由结论想到哪个定理?
线段垂直平分线的性质的逆定理
A
B
P
C
D
E
证明:连接PA、PB、PC.
∵ 点P在AB、AC的垂直平分线上(已知)
∴ PA=PB,PA=PC
(线段垂直平分线上的点与线段两端距离相等)
∴ PB=PC(等量代换)
∴ 点P在BC的垂直平分线上(与线段两端距离相等的点在这条线段的垂直平分线上)
你发现了什么结论?
三角形的三边的中垂线相交于一点,这点到三角形三个顶点的距离相等.
归纳
A
B
P
C
D
E
变式练习2 如图,A,B,C表示三个居民小区,为丰富居民的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在( )
A.AC,BC两边高线的交点处
B.AC,BC两边中线的交点处
C.AC,BC两边中垂线的交点处
D.∠A,∠B两内角平分线的交点处
C
B
A
C
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
A
2.已知线段AB,在平面上找到三个点D、E、F,使DA=DB,EA=EB,FA=FB,这样的点的组合共有( )种.
D
A.1 B.2 C.3 D.无数
随堂演练
3.如图,点D在△ABC的边BC上,且BC=BD+DA,则点D在线段( )的垂直平分线上.
A.AB
B.AC
C.BC
D.不能确定
B
D
C
B
A
4.下列说法:
①若点P、E是线段AB的垂直平分线上两点,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则经过点E的直线垂直平分线段AB.
其中正确的有 (填序号).
① ② ③
6.已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,∴∠DOE=∠COE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴△OED≌△OEC(AAS).
∴DO=CO,DE=CE.
∵EC⊥OA,ED⊥OB,∴∠EDO=∠ECO=90°.
课堂小结
线段的垂直平分的性质定理的逆定理
作用
内容
判断一个点是否在线段的垂直平分线上
到线段的两个端点距离相等的点在线段的垂直平分线上
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
