冀教版数学八年级上册同步课件:16.3 角平分线(共29张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:16.3 角平分线(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 678.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
第十六章 轴对称和中心对称
16.3 角的平分线
知识回顾
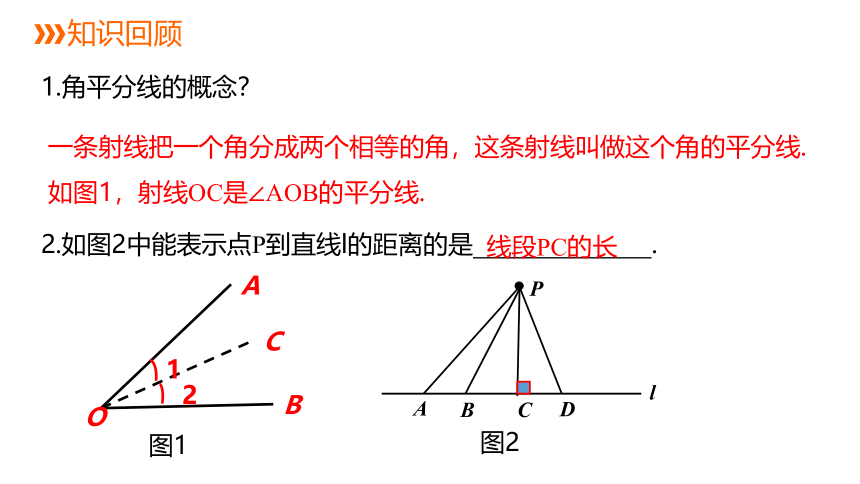
1.角平分线的概念?
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.如图1,射线OC是∠AOB的平分线.
O
B
C
A
1
2
2.如图2中能表示点P到直线l的距离的是 .
线段PC的长
P
l
A
B
C
D
图1
图2
情景导入
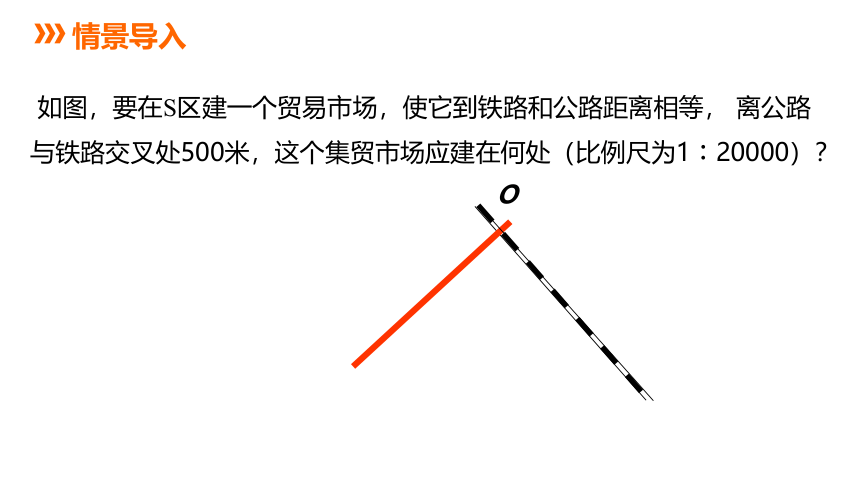
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
O
获取新知
知识点
角的平分线的性质定理
1
1.在一张半透明纸上画出一个角,将纸对折,使这个角的两边重合. 从中你能得出什么结论
一起探究
2.按图所示的过程,将你画出的∠AOB依上述办法对折后,设折痕为直线OC;再折纸,设折痕为直线n,直线n与边OA,OB分别交于点D,E,与折线OC交于点P;将纸展开铺平后,猜想线段PD与线段PE,线段OD与线段OE分别具有怎样的数量关系,并说明理由.
事实上,∠AOB是轴对称图形,它的平分线OC是对称轴.由折纸过程可知,PD=PE,特别地,当折痕n与OB垂直时,可得出:角平分线上的点到这个角的两边的距离相等.
下面就来证明折纸过程中发现的结论.
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
证明:在△PDO和△PEO中,
∵
∴ △PDO≌△PEO(AAS).
∴ PD=PE(全等三角形对应边相等).
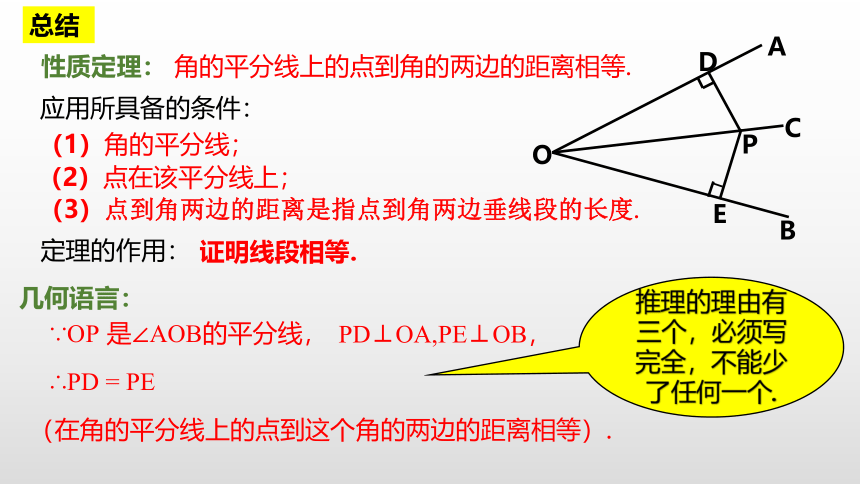
性质定理: 角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)点到角两边的距离是指点到角两边垂线段的长度.
定理的作用:
证明线段相等.
几何语言:
∵OP 是∠AOB的平分线,
∴PD = PE
(在角的平分线上的点到这个角的两边的距离相等).
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
总结
例1 已知:如图,在△ABC中,AD是它的角平分线且BD=CD∠B=∠C,DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE ≌ Rt△CDF.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
∴ Rt△BDE ≌ Rt△CDF.
∴ EB=FC.
BD=CD,
∠B=∠C,
∠DEB=∠DFC,
变式练习1 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )
A.1 B.2 C.4 D.8
B
解析:作PE⊥OA于E,如图,∵CP∥OB,∴∠ECP=∠AOB=30°,在Rt△EPC中,PE= PC= ×4=2,∵P是∠AOB平分线上一点,PE⊥OA,PD⊥OB,∴PD=PE=2.
温馨提示:1.求某点到一条直线的距离,若条件中有角平分线,则要想到角平分线的性质定理,转化为该点到另一边的距离.
2.过角平分线上一点作垂线段是解决有关角平分线问题最常用的作辅助线的方法.
知识点
角平分线性质定理的逆定理
2
1.写出角平分线的性质定理的逆命题.
2.根据这个逆命题的内容,画出图形.
3.结合图形,提出你对这个逆命题是否正确的猜想.
4.设法验证你的猜想.
做一做
思考:角平分线的性质定理的逆定理是真命题还是假命题呢?
角平分线的性质定理的逆定理
到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
几何语言:
∵ PD⊥OA,PE⊥OB,PD=PE,
∴点P 在∠AOB的平分线上.
例2 如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.
求证:AD平分∠BAC.
分析:要证AD平分∠BAC,已知条件中有两个垂直,即有点到角的两边的距离,再证这两个距离相等即可证明结论,证这两条垂线段相等,可通过证明△BDE和△CDF全等来完成.
∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,∵
∴△BDE≌△CDF(AAS),
∴DE=DF.
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC.
证明:
判定角平分线的两步:
(1)找出角的两边的垂线段;
(2)证明两条垂线段相等.
变式练习2 已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
D
E
F
A
B
C
P
N
M
思考:1.点P在∠A的平分线上吗?
点P在∠A的平分线上.
三角形的三条角平分线相交于一点,这一点到三角形三边的距离相等.
2.三角形的三条角平分线有什么关系?
获取新知
知识点
尺规作角的平分线
3
A
B
o
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
C
例3 如图,已知∠AOB.
求作:∠AOB的平分线.
A
B
M
N
C
思考:为什么OC是角平分线呢?
O
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
作图依据:作角平分线的理论根据是三角形全等的判定方法:SSS.
拓展:根据角平分线的作法可以作已知角的四等分线.
易错警示:作角平分线的最后一步“过两点作射线”时,不能简单地叙述为“连接两点”,连接两点是线段,角平分线是射线而不是线段.
1.作法中“以适当长为半径”的目的是为方便作图,不能太大或太小;“大于 EF的长为半径画弧”是因为若以小于或等于 EF的长为半径画弧时,画出的两弧不能相交或交点不明显.
归纳
例题讲解
变式练习3 如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
随堂演练
1.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .
60
BF
E
B
D
F
A
C
G
4.如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶ S△CAO=________________.
4∶5∶6
5.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠CDA的度数为________.
65°
6.如图,AP,CP分别是△ABC的外角∠MAC和∠NCA的平分线,它们交于点P,PD⊥BM于D,PF⊥BN于F.
求证:BP为∠MBN的平分线.
证明:
过P作PE⊥AC于点E,如图所示.
∵AP平分∠MAC,PD⊥AM,PE⊥AC,
∴PD=PE,
∵CP平分∠ACN,PF⊥CN,PE⊥AC,
∴PE=PF,∴PD=PF,
∴P在∠MBN的平分线上,
即BP为∠MBN的平分线.
7.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解:AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,即直线AD垂直平分线段EF.
A
B
C
D
E
F
课堂小结
角的平分线
尺规作图
性质定理
逆定理
到角的两边距离相等的点在角平分线上.
角平分线上的点到这个角的两边的距离相等.
第十六章 轴对称和中心对称
16.3 角的平分线
知识回顾
1.角平分线的概念?
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.如图1,射线OC是∠AOB的平分线.
O
B
C
A
1
2
2.如图2中能表示点P到直线l的距离的是 .
线段PC的长
P
l
A
B
C
D
图1
图2
情景导入
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
O
获取新知
知识点
角的平分线的性质定理
1
1.在一张半透明纸上画出一个角,将纸对折,使这个角的两边重合. 从中你能得出什么结论
一起探究
2.按图所示的过程,将你画出的∠AOB依上述办法对折后,设折痕为直线OC;再折纸,设折痕为直线n,直线n与边OA,OB分别交于点D,E,与折线OC交于点P;将纸展开铺平后,猜想线段PD与线段PE,线段OD与线段OE分别具有怎样的数量关系,并说明理由.
事实上,∠AOB是轴对称图形,它的平分线OC是对称轴.由折纸过程可知,PD=PE,特别地,当折痕n与OB垂直时,可得出:角平分线上的点到这个角的两边的距离相等.
下面就来证明折纸过程中发现的结论.
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
证明:在△PDO和△PEO中,
∵
∴ △PDO≌△PEO(AAS).
∴ PD=PE(全等三角形对应边相等).
性质定理: 角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)点到角两边的距离是指点到角两边垂线段的长度.
定理的作用:
证明线段相等.
几何语言:
∵OP 是∠AOB的平分线,
∴PD = PE
(在角的平分线上的点到这个角的两边的距离相等).
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
总结
例1 已知:如图,在△ABC中,AD是它的角平分线且BD=CD∠B=∠C,DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
分析:先利用角平分线的性质定理得到DE=DF,再利用全等证明Rt△BDE ≌ Rt△CDF.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
∴ Rt△BDE ≌ Rt△CDF.
∴ EB=FC.
BD=CD,
∠B=∠C,
∠DEB=∠DFC,
变式练习1 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )
A.1 B.2 C.4 D.8
B
解析:作PE⊥OA于E,如图,∵CP∥OB,∴∠ECP=∠AOB=30°,在Rt△EPC中,PE= PC= ×4=2,∵P是∠AOB平分线上一点,PE⊥OA,PD⊥OB,∴PD=PE=2.
温馨提示:1.求某点到一条直线的距离,若条件中有角平分线,则要想到角平分线的性质定理,转化为该点到另一边的距离.
2.过角平分线上一点作垂线段是解决有关角平分线问题最常用的作辅助线的方法.
知识点
角平分线性质定理的逆定理
2
1.写出角平分线的性质定理的逆命题.
2.根据这个逆命题的内容,画出图形.
3.结合图形,提出你对这个逆命题是否正确的猜想.
4.设法验证你的猜想.
做一做
思考:角平分线的性质定理的逆定理是真命题还是假命题呢?
角平分线的性质定理的逆定理
到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
几何语言:
∵ PD⊥OA,PE⊥OB,PD=PE,
∴点P 在∠AOB的平分线上.
例2 如图,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D.
求证:AD平分∠BAC.
分析:要证AD平分∠BAC,已知条件中有两个垂直,即有点到角的两边的距离,再证这两个距离相等即可证明结论,证这两条垂线段相等,可通过证明△BDE和△CDF全等来完成.
∵DF⊥AC于点F,DE⊥AB于点E,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,∵
∴△BDE≌△CDF(AAS),
∴DE=DF.
又∵DF⊥AC于点F,DE⊥AB于点E,
∴AD平分∠BAC.
证明:
判定角平分线的两步:
(1)找出角的两边的垂线段;
(2)证明两条垂线段相等.
变式练习2 已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
D
E
F
A
B
C
P
N
M
思考:1.点P在∠A的平分线上吗?
点P在∠A的平分线上.
三角形的三条角平分线相交于一点,这一点到三角形三边的距离相等.
2.三角形的三条角平分线有什么关系?
获取新知
知识点
尺规作角的平分线
3
A
B
o
M
N
C
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
C
例3 如图,已知∠AOB.
求作:∠AOB的平分线.
A
B
M
N
C
思考:为什么OC是角平分线呢?
O
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
作图依据:作角平分线的理论根据是三角形全等的判定方法:SSS.
拓展:根据角平分线的作法可以作已知角的四等分线.
易错警示:作角平分线的最后一步“过两点作射线”时,不能简单地叙述为“连接两点”,连接两点是线段,角平分线是射线而不是线段.
1.作法中“以适当长为半径”的目的是为方便作图,不能太大或太小;“大于 EF的长为半径画弧”是因为若以小于或等于 EF的长为半径画弧时,画出的两弧不能相交或交点不明显.
归纳
例题讲解
变式练习3 如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
随堂演练
1.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .
60
BF
E
B
D
F
A
C
G
4.如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶ S△CAO=________________.
4∶5∶6
5.如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠CDA的度数为________.
65°
6.如图,AP,CP分别是△ABC的外角∠MAC和∠NCA的平分线,它们交于点P,PD⊥BM于D,PF⊥BN于F.
求证:BP为∠MBN的平分线.
证明:
过P作PE⊥AC于点E,如图所示.
∵AP平分∠MAC,PD⊥AM,PE⊥AC,
∴PD=PE,
∵CP平分∠ACN,PF⊥CN,PE⊥AC,
∴PE=PF,∴PD=PF,
∴P在∠MBN的平分线上,
即BP为∠MBN的平分线.
7.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解:AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,即直线AD垂直平分线段EF.
A
B
C
D
E
F
课堂小结
角的平分线
尺规作图
性质定理
逆定理
到角的两边距离相等的点在角平分线上.
角平分线上的点到这个角的两边的距离相等.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
