冀教版数学八年级上册同步课件:17.2 直角三角形(共28张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:17.2 直角三角形(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 16:31:46 | ||
图片预览







文档简介
(共28张PPT)
第十七章 特殊三角形
17.2 直角三角形
下面几幅图都是用七巧板拼成的,你能从中找出多少个直角三角形呢?
1.问题:什么叫做直角三角形?
2.请同学们交流、合作完成本题。
情景导入
3x+5y+2z
x2+2x+18
t-5
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
获取新知
一起探究
定 义:
像这由单项式相加组成的代数式叫做多项式.
直角三角形的性质与判定
问题1 已知一个直角三角形,有一个角为直角,根据三角形内角和定理我们可以得到什么结论?
A
B
C
提示:三角形的三个内角和为180°,已知一个角为直角,可以得到另外两个角的数量关系
获取新知
一起探究
直角三角形的性质与判定
A
B
C
在直角三角形ABC中,∠C=90°由三角形内角和定理,得∠A +∠B+∠C=180°,
即∠A +∠B=90°.
归纳:直角三角形的性质定理:
直角三角形的两个锐角互余.
直角三角形性质的应用格式:
在直角三角形ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =____.
直角三角形的表示方法:
直角三角形可以用符号“______”表示,直角三角形ABC 可以写成___ ____ .
90°
Rt△
Rt△ABC
归 纳
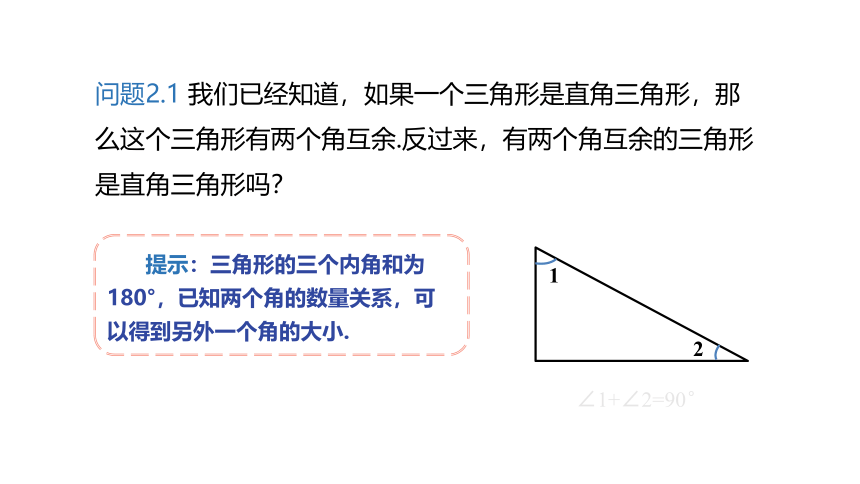
问题2.1 我们已经知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?
1
2
∠1+∠2=90°
提示:三角形的三个内角和为180°,已知两个角的数量关系,可以得到另外一个角的大小.
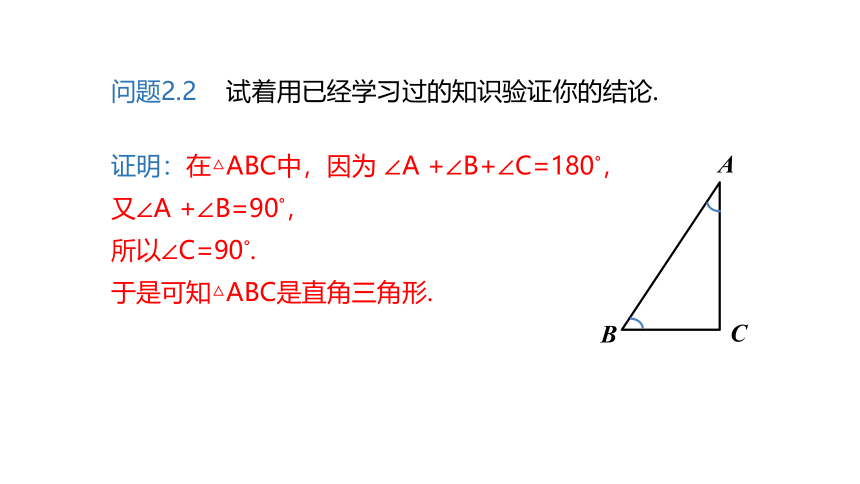
问题2.2 试着用已经学习过的知识验证你的结论.
证明:在△ABC中,因为 ∠A +∠B+∠C=180°,
又∠A +∠B=90°,
所以∠C=90°.
于是可知△ABC是直角三角形.
A
B
C
直角三角形的判定定理:
如果一个三角形的两个角_____,那么这个三角形是直 角三角形.
直角三角形判定定理的应用格式:
在三角形ABC 中,
∵∠A +∠B =____,
∴三角形ABC 是___________ .
互余
90°
直角三角形
归 纳
直角三角形斜边上的中线性质
问题1 在一张半透明的纸上画出Rt△ABC,∠C=90°,如图(1);
B
A
C
E
F
(B)
将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE, 如图(2);
将纸展开,如图(3) .
B
A
C
(1)
(2)
B
A
C
E
F
(3)
获取新知
问题2 (1)∠ECF与∠B有怎样的关系?线段EC与线段EB有怎样的关系?
∠ECF=∠B
EC=EB
(2)由发现的上述关系以及∠A+∠B=∠ACB,∠ACE+∠ECF=∠ACB,你能判断∠ACE与∠A的大小关系吗?线段AE与线段CE呢
∠ACE=∠A
AE=CE
(3)由发现的上述关系,你能猜想线段CE与线段AB的关系吗
猜想:CE=AE=EB,即CE是AB的中线,且CE= AB.
问题3 试着运用所学知识,验证你的猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD 是斜边AB上的中线.
求证:CD= AB.
B
A
C
D
证明:如图,过点D,作DE∥BC,交AC于点E;
作DF∥AC,交BC于点F.
在△AED 和△DFB 中,
∠A=∠FDB(两直线平行,同位角相等),
∵ AD=DB(中线的概念),
∠ADE=∠B(两直线平行,同位角相等),
∴△AED≌△DFB (ASA).
∴QE=DF,ED=FB. (全等三角形的对应边相等)
F
E
B
A
C
D
F
E
B
A
C
D
同理可证,△CDE≌△DCF.
从而,ED=FC,EC=FD.
∴ AE=EC,CF=FB.(等量代换)
又∵DE⊥AC,DF⊥BC,(两直线平行,同位角相等)
∴DE为AC的垂直平分线,
DF为BC的垂直平分线.
∴AD=CD=BD(线段垂直平分线的性质定理).
CD= AB.
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
数学语言表述为:
在Rt△ABC中
∵CD是斜边AB上的中线
∴CD=AD=BD= AB
(直角三角形斜边上的中线等于斜边的一半)
同学们能用语言表达刚才的发现吗?请同学们试着说一说。
含30°角的直角三角形的性质
问题1:
用刻度尺测量含30°角的直角三角形斜边和短直角边,比较它们之间的数量关系.
短直角边= ×斜边
获取新知
问题2 如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
分离
拼接
问题3 将做好的等边三角形纸片,沿一边上的高对折,如图所示:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
∴ BC = AB.
1.具备下列条件的△ABC中,不是直角三角形的是 ( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
随堂演练
2.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=26°,则∠BDC的度数是( )
A.26°
B.38°
C.42°
D.52°
D
3.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
B
4.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.20
B.18
C.14
D.13
C
5.如图:在Rt△ABC中∠A=300,AB+BC=12cm,则AB=_____cm
C
B
A
300
8
6.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,BD=____, BE=____ .
A
C
E
B
D
4cm
2cm
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
8.如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由.
证明:相等.理由如下∵AD⊥BD,AC⊥BC,
∴∠ADB=∠BCA=90°,
∵E为AB的中点,
∴DE=CE.
∴DE= AB,CE= AB.
直角三角形
性质定理
直角三角形的两个锐角互余
判定定理
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半
在直角三角形中,30°角所对的直角边等于斜边的一半
课堂小结
第十七章 特殊三角形
17.2 直角三角形
下面几幅图都是用七巧板拼成的,你能从中找出多少个直角三角形呢?
1.问题:什么叫做直角三角形?
2.请同学们交流、合作完成本题。
情景导入
3x+5y+2z
x2+2x+18
t-5
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
获取新知
一起探究
定 义:
像这由单项式相加组成的代数式叫做多项式.
直角三角形的性质与判定
问题1 已知一个直角三角形,有一个角为直角,根据三角形内角和定理我们可以得到什么结论?
A
B
C
提示:三角形的三个内角和为180°,已知一个角为直角,可以得到另外两个角的数量关系
获取新知
一起探究
直角三角形的性质与判定
A
B
C
在直角三角形ABC中,∠C=90°由三角形内角和定理,得∠A +∠B+∠C=180°,
即∠A +∠B=90°.
归纳:直角三角形的性质定理:
直角三角形的两个锐角互余.
直角三角形性质的应用格式:
在直角三角形ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =____.
直角三角形的表示方法:
直角三角形可以用符号“______”表示,直角三角形ABC 可以写成___ ____ .
90°
Rt△
Rt△ABC
归 纳
问题2.1 我们已经知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?
1
2
∠1+∠2=90°
提示:三角形的三个内角和为180°,已知两个角的数量关系,可以得到另外一个角的大小.
问题2.2 试着用已经学习过的知识验证你的结论.
证明:在△ABC中,因为 ∠A +∠B+∠C=180°,
又∠A +∠B=90°,
所以∠C=90°.
于是可知△ABC是直角三角形.
A
B
C
直角三角形的判定定理:
如果一个三角形的两个角_____,那么这个三角形是直 角三角形.
直角三角形判定定理的应用格式:
在三角形ABC 中,
∵∠A +∠B =____,
∴三角形ABC 是___________ .
互余
90°
直角三角形
归 纳
直角三角形斜边上的中线性质
问题1 在一张半透明的纸上画出Rt△ABC,∠C=90°,如图(1);
B
A
C
E
F
(B)
将∠B折叠,使点B与点C重合,折痕为EF,沿BE画出虚线CE, 如图(2);
将纸展开,如图(3) .
B
A
C
(1)
(2)
B
A
C
E
F
(3)
获取新知
问题2 (1)∠ECF与∠B有怎样的关系?线段EC与线段EB有怎样的关系?
∠ECF=∠B
EC=EB
(2)由发现的上述关系以及∠A+∠B=∠ACB,∠ACE+∠ECF=∠ACB,你能判断∠ACE与∠A的大小关系吗?线段AE与线段CE呢
∠ACE=∠A
AE=CE
(3)由发现的上述关系,你能猜想线段CE与线段AB的关系吗
猜想:CE=AE=EB,即CE是AB的中线,且CE= AB.
问题3 试着运用所学知识,验证你的猜想.
已知:如图,在Rt△ABC中,∠ACB=90°,CD 是斜边AB上的中线.
求证:CD= AB.
B
A
C
D
证明:如图,过点D,作DE∥BC,交AC于点E;
作DF∥AC,交BC于点F.
在△AED 和△DFB 中,
∠A=∠FDB(两直线平行,同位角相等),
∵ AD=DB(中线的概念),
∠ADE=∠B(两直线平行,同位角相等),
∴△AED≌△DFB (ASA).
∴QE=DF,ED=FB. (全等三角形的对应边相等)
F
E
B
A
C
D
F
E
B
A
C
D
同理可证,△CDE≌△DCF.
从而,ED=FC,EC=FD.
∴ AE=EC,CF=FB.(等量代换)
又∵DE⊥AC,DF⊥BC,(两直线平行,同位角相等)
∴DE为AC的垂直平分线,
DF为BC的垂直平分线.
∴AD=CD=BD(线段垂直平分线的性质定理).
CD= AB.
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
数学语言表述为:
在Rt△ABC中
∵CD是斜边AB上的中线
∴CD=AD=BD= AB
(直角三角形斜边上的中线等于斜边的一半)
同学们能用语言表达刚才的发现吗?请同学们试着说一说。
含30°角的直角三角形的性质
问题1:
用刻度尺测量含30°角的直角三角形斜边和短直角边,比较它们之间的数量关系.
短直角边= ×斜边
获取新知
问题2 如图,将两个含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
分离
拼接
问题3 将做好的等边三角形纸片,沿一边上的高对折,如图所示:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
∴ BC = AB.
1.具备下列条件的△ABC中,不是直角三角形的是 ( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
随堂演练
2.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=26°,则∠BDC的度数是( )
A.26°
B.38°
C.42°
D.52°
D
3.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
B
4.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.20
B.18
C.14
D.13
C
5.如图:在Rt△ABC中∠A=300,AB+BC=12cm,则AB=_____cm
C
B
A
300
8
6.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,BD=____, BE=____ .
A
C
E
B
D
4cm
2cm
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
8.如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由.
证明:相等.理由如下∵AD⊥BD,AC⊥BC,
∴∠ADB=∠BCA=90°,
∵E为AB的中点,
∴DE=CE.
∴DE= AB,CE= AB.
直角三角形
性质定理
直角三角形的两个锐角互余
判定定理
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半
在直角三角形中,30°角所对的直角边等于斜边的一半
课堂小结
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
