冀教版数学八年级上册同步课件:16.1 轴对称(共34张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:16.1 轴对称(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
第十六章 轴对称和中心对称
16.1 轴对称
知识回顾
1.如图,把一张纸对折,根据自己的喜好剪出图案(折痕处不要完全剪断),打开这张纸,得到一个美丽的窗花,多做几个这样的窗花,你能发现这些窗花有什么共同特点吗?
能够完全重合的两个图形叫做图形.
它们是全等图形.
2.什么叫做全等形?
情景导入
图片欣赏
这些图形有什么共同的特点?
这些图形有什么共同的特点?
图片欣赏
观察
每幅图形沿着虚线折叠,虚线两旁的部分能够完全重合.
a
m
获取新知
概念学习
知识点
轴对称图形和轴对称
1
1.轴对称图形: 一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.
轴对称给我们带来美的感受,对称现象无处不在,从自然景观到艺术品,从建筑到交通标志,从汉字到英语字母,还有生活用品,都可以找到轴对称的现象.
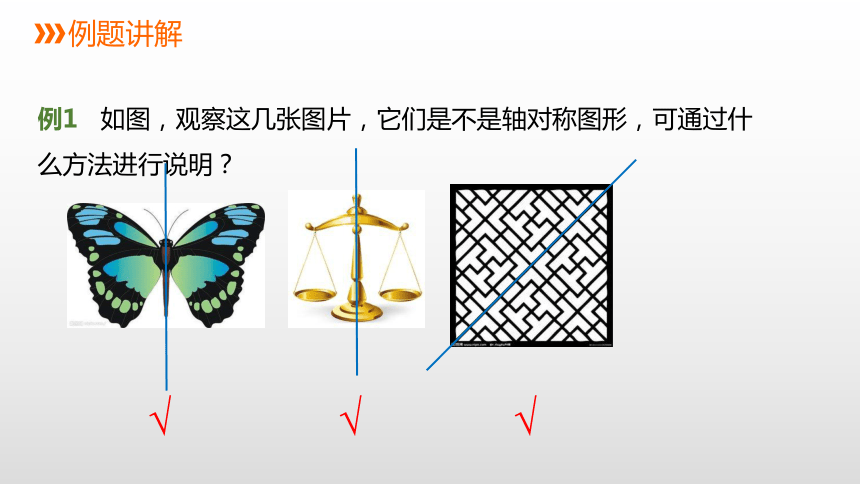
例1 如图,观察这几张图片,它们是不是轴对称图形,可通过什么方法进行说明?
√
√
√
例题讲解
判断轴对称图形的方法:
根据图形的特征,尝试找到一条直线,沿着这条直线对折,如果直线两边的部分能够重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
注意:尝试多角度来观察图形和对折图形.
归纳
变式练习1 汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性.在下列四个汉字中,不是轴对称图形的是( )
D
2.轴对称:一般地,如果两个图形沿某条直线对折后,这两个图形能够完全重合,那么我们就说这两个图形成轴对称,这条直线叫做对称轴.
关于对称轴对称的点、对称的线段、对称的角分别叫做对应点、
对应线段、对应角.
轴对称的定义包含两层含义:
(1)有两个图形,且形状、大小完全相同.
(2)两个图形的位置必须满足沿一条直线对折后能完全重合.
A
C'
B'
A'
C
B
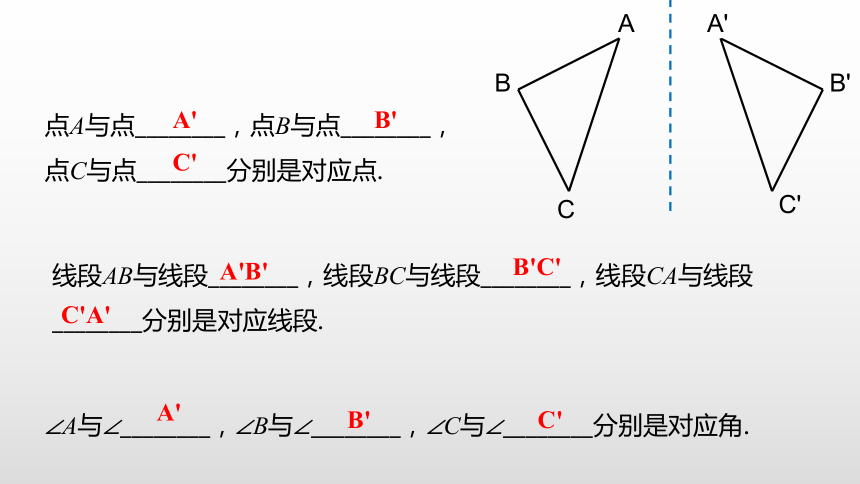
点A与点________,点B与点________,点C与点________分别是对应点.
A'
B'
C'
线段AB与线段________,线段BC与线段________,线段CA与线段________分别是对应线段.
A'B'
B'C'
C'A'
∠A与∠________,∠B与∠________,∠C与∠________分别是对应角.
A'
B'
C'
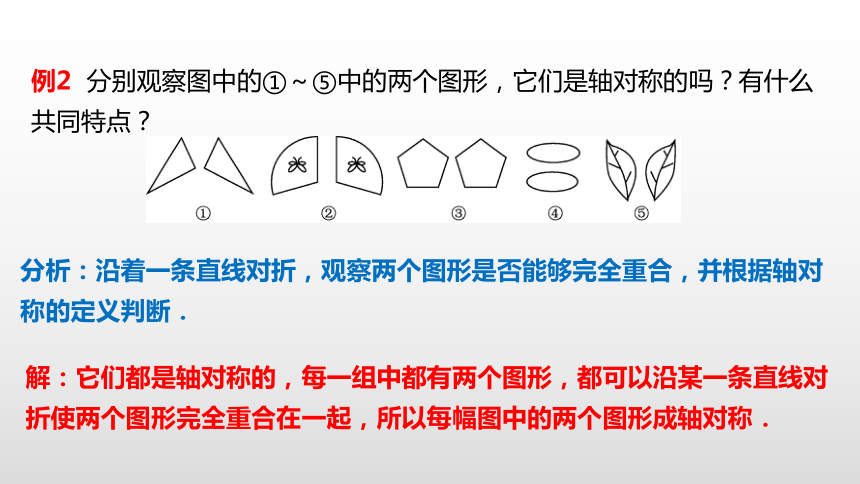
例2 分别观察图中的①~⑤中的两个图形,它们是轴对称的吗?有什么共同特点?
分析:沿着一条直线对折,观察两个图形是否能够完全重合,并根据轴对称的定义判断.
解:它们都是轴对称的,每一组中都有两个图形,都可以沿某一条直线对折使两个图形完全重合在一起,所以每幅图中的两个图形成轴对称.
变式练习2 下列说法正确的是( ).
A.能够完全重合的两个图形成轴对称.
B.全等的两个图形成轴对称.
C.形状一样的两个图形成轴对称.
D.沿着一条直线对折能够重合的两个图形成轴对称.
D
识别轴对称的方法:
判断两个图形是否关于某条直线成轴对称,先观察两个图形的形状、大小,如果形状、大小相同,再看能否找到一条直线且将两个图形沿这条直线对折,如果能够重合,则这两个图形成轴对称,否则不成轴对称.
归纳
3.轴对称图形与轴对称的区别与联系
轴对称图形 轴对称
区别 本质不同 具有特殊形状的图形 两个图形之间的对称关系
对象不同 一个图形 两个图形
对称轴的位置不同 过图形的某条直线 在两个图形之间
对称轴的数量不同 不一定只有一条 只有一条对称轴
联 系 (1)沿对称轴折叠,图形的两部分重合 (2)如果把轴对称图形对称轴两边的部分看作两个图形,那么这两个图形成轴对称 (1)沿对称轴折叠,两个图形重合
(2)如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形
名 称
关 系
如图,当我们把两扇门看做一个图形的时候,整个图形是一个轴对称图形,当我们把两扇门看做两个图形的时候,这两个扇门关于中间的一条线成轴对称.
知识点
轴对称的性质
2
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点.
(1)线段AA′,BB′,CC′与直线MN有什么位置关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
(2)线段AB与A′B′,BC与B′C′,AC与A′C′有什么数量关系?
(3)∠A与∠A'有什么关系?∠B与∠B'呢?∠C与∠C'呢?
AB =A′B′,BC=B′C′,AC=A′C′.
∠A=∠A',∠B=∠B',∠C=∠C'.
A
B
C
A′
B′
C′
N
M
(4)△ABC和△A′B′C′全等吗?
△ABC≌△A'B'C'
归纳
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
成轴对称图形的性质对于轴对称图形同样适用.
垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
线段是轴对称图形,线段的中垂线是它的对称轴.
概念学习
例3 如图是轴对称图形,图中直线l是它的对称轴.
(1)∠3和∠4有什么关系?AB与A′B′呢?为什么?
(2)DD′与直线l 有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
解:(1)∠3=∠4,AB=A′B′,因为轴对称图形中对应角相等,对应线段相等.
(2)直线l是DD′的垂直平分线,因为轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(3)AD=A′D′,∠1=∠2,DC=D′C′等.
变式练习3 如图,正方形ABCD的边长为4cm,则图中阴影部分
的面积为( )
A.4cm2 B.8cm2
C.12cm2 D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).
B
【名师点睛】正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
知识点
轴对称作图
3
例4 如图,已知线段AB和直线l,画出线段AB关于直线l的对称线段.
解:如图 .
(1)分别过点A和点B画直线l的垂线段AO和BO′,垂足分别为 O和O′ .
(2)分别延长AO到点A′,BO′到点B′,使AO′= AO,B′O′=BO′.
(3)连接A′B′.
线段A′B′即为所求.
作一个图形的对称图形就是作各个顶点关于对称轴的对称点,把作对称图形的问题可以转化为作点的对称点的问题.
归纳
变式练习4 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
作法:(1)过点A画直线l的垂线,垂足为点
O,在垂线上截取OA′=OA,A′就是点A关于
直线l的对称点.
(2)同理,分别画出点B,C关于直线l的
对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
A
B
C
A′
B′
C′
O
试一试:画好后,用折叠的办法验证一下你的结果.
随堂演练
2.下列各组图形:①任意两个半径相等的圆;②正方形的一条对角线把一个正方形分成的两个三角形;③长方形的一条对角线把长方形分成的两个三角形;④两个全等的三角形.其中,一定成轴对称的图形有( )
A.1组 B.2组 C.3组 D.4组
B
在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
B
3.把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后的图形是( )
C
4.如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
5.如图,将长方形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=50°,则∠CFD的度数为( )
A.20°
B.30°
C.40°
D.50°
C
【名师点睛】折叠是一种轴对称变换,折叠前后的图形形状和大小不变,对应边和对应角相等.
7.如图,画△ABC关于直线m的对称图形.
m
A
B
C
(A ′)
C ′
B ′
6.一辆汽车的车牌号在水中的倒影是: ,那么它的实际车牌号
是: .
K62897
解:如图.
8.如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴.
整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
9.请你利用一个等腰三角形、两个长方形、三个圆,设计一些具有轴对称特征的图案, 并用简练的文字说明你的创意.
华灯初上
小女孩
课堂小结
沿直线对
折重合
轴对称图形与
轴对称的联系
一般地,如果两个图形沿某条直线对折后,这两个图形能完全重合,那么我们就说这两个图形成轴对称
轴对称图形
如果两个图形关于某一条直线成轴对称,那么这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
轴对称
把成轴对称的两个图形看成一整体,它就是一个轴对称图形。把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形
第十六章 轴对称和中心对称
16.1 轴对称
知识回顾
1.如图,把一张纸对折,根据自己的喜好剪出图案(折痕处不要完全剪断),打开这张纸,得到一个美丽的窗花,多做几个这样的窗花,你能发现这些窗花有什么共同特点吗?
能够完全重合的两个图形叫做图形.
它们是全等图形.
2.什么叫做全等形?
情景导入
图片欣赏
这些图形有什么共同的特点?
这些图形有什么共同的特点?
图片欣赏
观察
每幅图形沿着虚线折叠,虚线两旁的部分能够完全重合.
a
m
获取新知
概念学习
知识点
轴对称图形和轴对称
1
1.轴对称图形: 一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.
轴对称给我们带来美的感受,对称现象无处不在,从自然景观到艺术品,从建筑到交通标志,从汉字到英语字母,还有生活用品,都可以找到轴对称的现象.
例1 如图,观察这几张图片,它们是不是轴对称图形,可通过什么方法进行说明?
√
√
√
例题讲解
判断轴对称图形的方法:
根据图形的特征,尝试找到一条直线,沿着这条直线对折,如果直线两边的部分能够重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
注意:尝试多角度来观察图形和对折图形.
归纳
变式练习1 汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性.在下列四个汉字中,不是轴对称图形的是( )
D
2.轴对称:一般地,如果两个图形沿某条直线对折后,这两个图形能够完全重合,那么我们就说这两个图形成轴对称,这条直线叫做对称轴.
关于对称轴对称的点、对称的线段、对称的角分别叫做对应点、
对应线段、对应角.
轴对称的定义包含两层含义:
(1)有两个图形,且形状、大小完全相同.
(2)两个图形的位置必须满足沿一条直线对折后能完全重合.
A
C'
B'
A'
C
B
点A与点________,点B与点________,点C与点________分别是对应点.
A'
B'
C'
线段AB与线段________,线段BC与线段________,线段CA与线段________分别是对应线段.
A'B'
B'C'
C'A'
∠A与∠________,∠B与∠________,∠C与∠________分别是对应角.
A'
B'
C'
例2 分别观察图中的①~⑤中的两个图形,它们是轴对称的吗?有什么共同特点?
分析:沿着一条直线对折,观察两个图形是否能够完全重合,并根据轴对称的定义判断.
解:它们都是轴对称的,每一组中都有两个图形,都可以沿某一条直线对折使两个图形完全重合在一起,所以每幅图中的两个图形成轴对称.
变式练习2 下列说法正确的是( ).
A.能够完全重合的两个图形成轴对称.
B.全等的两个图形成轴对称.
C.形状一样的两个图形成轴对称.
D.沿着一条直线对折能够重合的两个图形成轴对称.
D
识别轴对称的方法:
判断两个图形是否关于某条直线成轴对称,先观察两个图形的形状、大小,如果形状、大小相同,再看能否找到一条直线且将两个图形沿这条直线对折,如果能够重合,则这两个图形成轴对称,否则不成轴对称.
归纳
3.轴对称图形与轴对称的区别与联系
轴对称图形 轴对称
区别 本质不同 具有特殊形状的图形 两个图形之间的对称关系
对象不同 一个图形 两个图形
对称轴的位置不同 过图形的某条直线 在两个图形之间
对称轴的数量不同 不一定只有一条 只有一条对称轴
联 系 (1)沿对称轴折叠,图形的两部分重合 (2)如果把轴对称图形对称轴两边的部分看作两个图形,那么这两个图形成轴对称 (1)沿对称轴折叠,两个图形重合
(2)如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形
名 称
关 系
如图,当我们把两扇门看做一个图形的时候,整个图形是一个轴对称图形,当我们把两扇门看做两个图形的时候,这两个扇门关于中间的一条线成轴对称.
知识点
轴对称的性质
2
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点.
(1)线段AA′,BB′,CC′与直线MN有什么位置关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
(2)线段AB与A′B′,BC与B′C′,AC与A′C′有什么数量关系?
(3)∠A与∠A'有什么关系?∠B与∠B'呢?∠C与∠C'呢?
AB =A′B′,BC=B′C′,AC=A′C′.
∠A=∠A',∠B=∠B',∠C=∠C'.
A
B
C
A′
B′
C′
N
M
(4)△ABC和△A′B′C′全等吗?
△ABC≌△A'B'C'
归纳
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
成轴对称图形的性质对于轴对称图形同样适用.
垂直且平分一条线段的直线,叫做这条线段的垂直平分线,简称中垂线.
线段是轴对称图形,线段的中垂线是它的对称轴.
概念学习
例3 如图是轴对称图形,图中直线l是它的对称轴.
(1)∠3和∠4有什么关系?AB与A′B′呢?为什么?
(2)DD′与直线l 有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
解:(1)∠3=∠4,AB=A′B′,因为轴对称图形中对应角相等,对应线段相等.
(2)直线l是DD′的垂直平分线,因为轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线.
(3)AD=A′D′,∠1=∠2,DC=D′C′等.
变式练习3 如图,正方形ABCD的边长为4cm,则图中阴影部分
的面积为( )
A.4cm2 B.8cm2
C.12cm2 D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).
B
【名师点睛】正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
知识点
轴对称作图
3
例4 如图,已知线段AB和直线l,画出线段AB关于直线l的对称线段.
解:如图 .
(1)分别过点A和点B画直线l的垂线段AO和BO′,垂足分别为 O和O′ .
(2)分别延长AO到点A′,BO′到点B′,使AO′= AO,B′O′=BO′.
(3)连接A′B′.
线段A′B′即为所求.
作一个图形的对称图形就是作各个顶点关于对称轴的对称点,把作对称图形的问题可以转化为作点的对称点的问题.
归纳
变式练习4 如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
作法:(1)过点A画直线l的垂线,垂足为点
O,在垂线上截取OA′=OA,A′就是点A关于
直线l的对称点.
(2)同理,分别画出点B,C关于直线l的
对称点B′,C′ .
(3)连接A′B′,B′C′,C′A′,得到△A′B′C′即为所求.
A
B
C
A′
B′
C′
O
试一试:画好后,用折叠的办法验证一下你的结果.
随堂演练
2.下列各组图形:①任意两个半径相等的圆;②正方形的一条对角线把一个正方形分成的两个三角形;③长方形的一条对角线把长方形分成的两个三角形;④两个全等的三角形.其中,一定成轴对称的图形有( )
A.1组 B.2组 C.3组 D.4组
B
在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )
B
3.把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后的图形是( )
C
4.如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
5.如图,将长方形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=50°,则∠CFD的度数为( )
A.20°
B.30°
C.40°
D.50°
C
【名师点睛】折叠是一种轴对称变换,折叠前后的图形形状和大小不变,对应边和对应角相等.
7.如图,画△ABC关于直线m的对称图形.
m
A
B
C
(A ′)
C ′
B ′
6.一辆汽车的车牌号在水中的倒影是: ,那么它的实际车牌号
是: .
K62897
解:如图.
8.如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴.
整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
9.请你利用一个等腰三角形、两个长方形、三个圆,设计一些具有轴对称特征的图案, 并用简练的文字说明你的创意.
华灯初上
小女孩
课堂小结
沿直线对
折重合
轴对称图形与
轴对称的联系
一般地,如果两个图形沿某条直线对折后,这两个图形能完全重合,那么我们就说这两个图形成轴对称
轴对称图形
如果两个图形关于某一条直线成轴对称,那么这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
轴对称
把成轴对称的两个图形看成一整体,它就是一个轴对称图形。把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
