冀教版数学八年级上册同步课件:17.3.1 勾股定理(共24张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:17.3.1 勾股定理(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 16:54:28 | ||
图片预览



文档简介
(共24张PPT)
第十七章 有理数
课堂小结
例题讲解
获取新知
随堂演练
情景导入
17.3.1 勾股定理
大会会标
情景导入
北京欢迎你
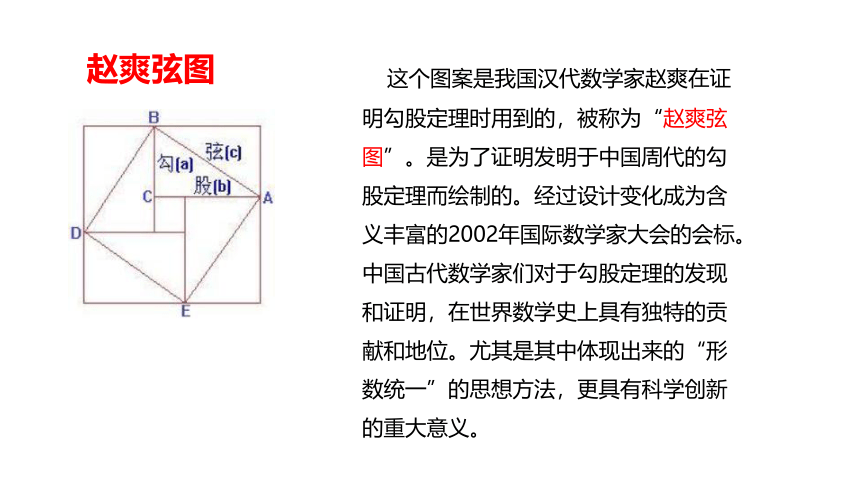
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”。是为了证明发明于中国周代的勾股定理而绘制的。经过设计变化成为含义丰富的2002年国际数学家大会的会标。中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位。尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。
赵爽弦图
3
5
4
9
16
25
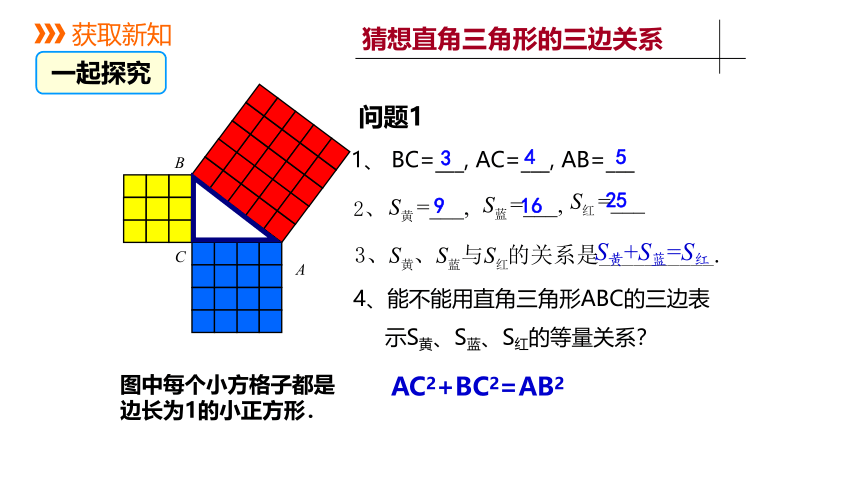
问题1
1、 BC=___, AC=___, AB=___
2、
4、能不能用直角三角形ABC的三边表
示S黄、S蓝、S红的等量关系?
S黄+S蓝=S红
AC2+BC2=AB2
图中每个小方格子都是边长为1的小正方形.
B
C
A
猜想直角三角形的三边关系
获取新知
一起探究
A
C
B
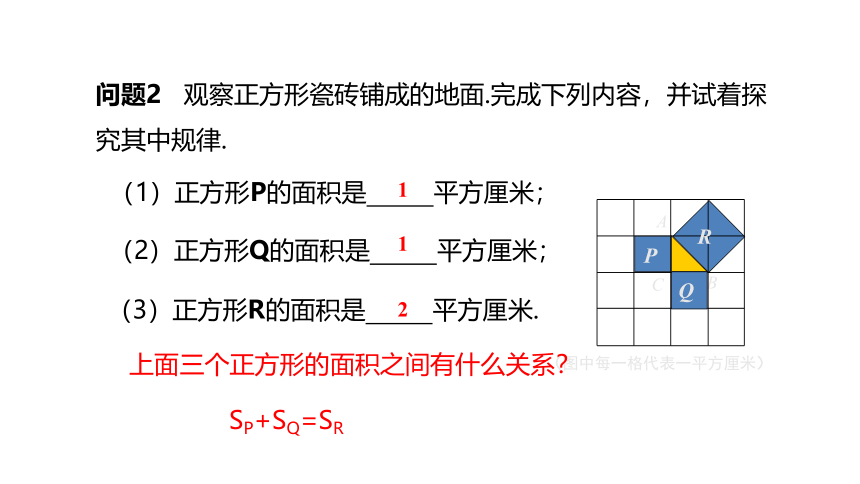
问题2 观察正方形瓷砖铺成的地面.完成下列内容,并试着探究其中规律.
(图中每一格代表一平方厘米)
P
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
上面三个正方形的面积之间有什么关系?
Q
R
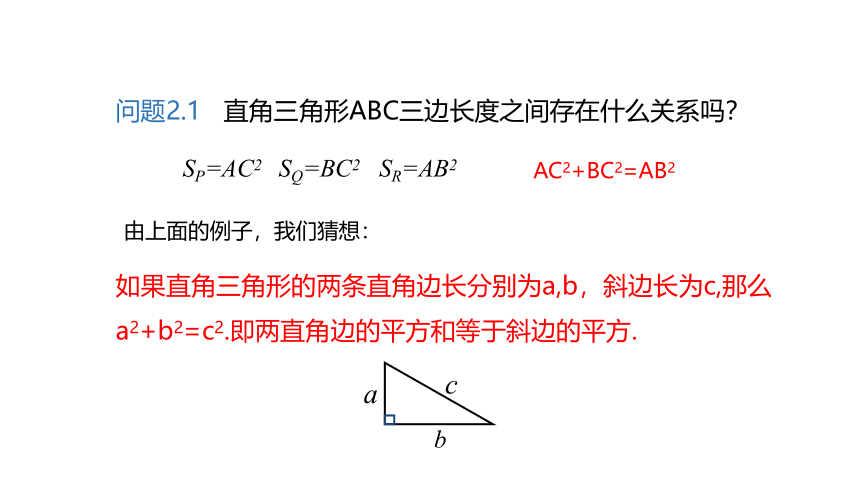
问题2.1 直角三角形ABC三边长度之间存在什么关系吗?
AC2+BC2=AB2
SP=AC2 SQ=BC2 SR=AB2
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.即两直角边的平方和等于斜边的平方.
由上面的例子,我们猜想:
a
b
c
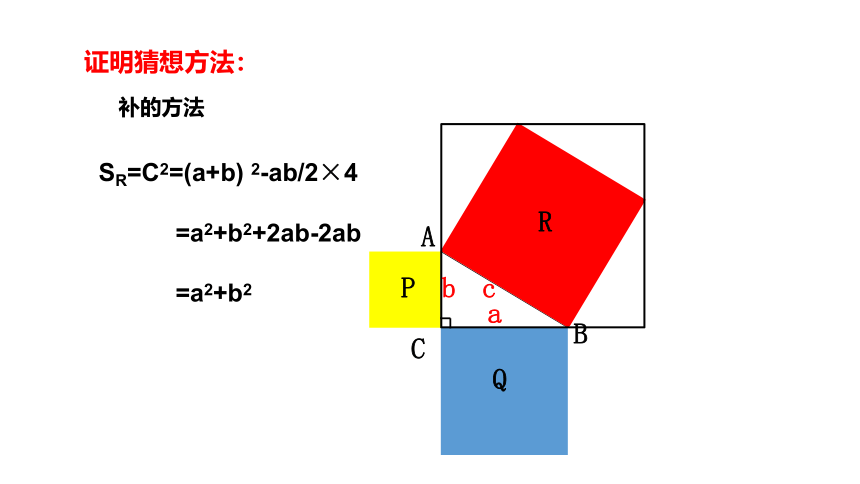
证明猜想方法:
A
B
C
补的方法
P
Q
R
SR=C2=(a+b) 2-ab/2×4
=a2+b2+2ab-2ab
=a2+b2
b
a
c
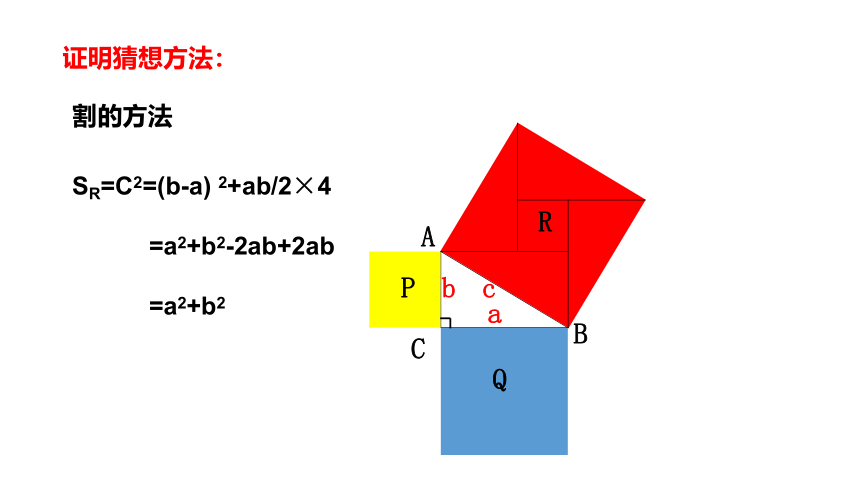
证明猜想方法:
A
B
C
割的方法
P
Q
R
SR=C2=(b-a) 2+ab/2×4
=a2+b2-2ab+2ab
=a2+b2
b
a
c
勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
A
B
C
勾
股
弦
归纳:如图,我国古代把直角三角形较短的直角边叫做“勾”,较长的直角边叫做“股”,斜边叫做“弦”.因此,直角三角形三边之间的关系称为勾股定理 .
由前面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a,b,斜边为c,那么一定有a2+b2=c2.
a
A
B
C
b
c
∟
几何语言:
∴a2+b2=c2(勾股定理).
∵在Rt△ABC中 ,∠C=90°,
勾股定理揭示了直角三角形三边之间的关系.
例 1 观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P 的面积为9,正方形Q 的面积为15,则正方形M 的面积为______;
(2)如图②,分别以直角三角形ABC 的
三边长为直径向三角形外作三个半圆,
则这三个半圆形的面积之间的关系式是
.(用图中字母表示)
例题讲解
勾股定理与图形面积
归纳:
与直角三角形三边相连的正方形、半圆及正多边形、圆都具有相同的结论:
两直角边上图形面积的和等于斜边上图形的面积.
本例考查了勾股定理及半圆面积的求法,解答此类题目的关键是仔细观察所给图形,面积与边长、直径有平方关系,就很容易联想到勾股定理.
【跟踪训练】
求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144=x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5
例2 如图,在Rt△ABC中, ∠C=90°.
C
A
B
(1)若a=1,b=2,求c.
(2)若a=15,c=17,求b.
解:
(1)据勾股定理,得
∵c>0
(2)据勾股定理得
∵b>0
【变式题】 在Rt△ABC中,AB=4,AC=3,求BC的长.
4
3
C
A
B
图
4
3
A
C
B
图
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
方法点拨:已知直角三角形的两边求第三边,关键是先明确所求的边是直角边还是斜边,再应用勾股定理.
1.直角三角形ABC的两直角边BC=12,AC=16,则
△ABC的斜边AB的长是 ( )
A.20 B.10 C.9.6 D.8
A
随堂演练
2.下图中,不能用来证明勾股定理的是( )
D
3.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
4.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
5.若直角三角形中,有两边长是5和7,则第三边长的平方为_________.
17
5
74或24
6.已知∠ACB=90°,CD⊥AB,AC=3,BC=4. 求CD的长.
A
D
B
C
3
4
解:因为∠ACB=90°,AC=3,BC=4,
所以AB2=AC2+BC2=25,即AB=5.
根据三角形面积公式,
AC×BC= AB×CD.
所以CD= .
7. 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16;
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.
∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
总结:题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.
课堂小结
第十七章 有理数
课堂小结
例题讲解
获取新知
随堂演练
情景导入
17.3.1 勾股定理
大会会标
情景导入
北京欢迎你
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”。是为了证明发明于中国周代的勾股定理而绘制的。经过设计变化成为含义丰富的2002年国际数学家大会的会标。中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位。尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。
赵爽弦图
3
5
4
9
16
25
问题1
1、 BC=___, AC=___, AB=___
2、
4、能不能用直角三角形ABC的三边表
示S黄、S蓝、S红的等量关系?
S黄+S蓝=S红
AC2+BC2=AB2
图中每个小方格子都是边长为1的小正方形.
B
C
A
猜想直角三角形的三边关系
获取新知
一起探究
A
C
B
问题2 观察正方形瓷砖铺成的地面.完成下列内容,并试着探究其中规律.
(图中每一格代表一平方厘米)
P
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
上面三个正方形的面积之间有什么关系?
Q
R
问题2.1 直角三角形ABC三边长度之间存在什么关系吗?
AC2+BC2=AB2
SP=AC2 SQ=BC2 SR=AB2
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.即两直角边的平方和等于斜边的平方.
由上面的例子,我们猜想:
a
b
c
证明猜想方法:
A
B
C
补的方法
P
Q
R
SR=C2=(a+b) 2-ab/2×4
=a2+b2+2ab-2ab
=a2+b2
b
a
c
证明猜想方法:
A
B
C
割的方法
P
Q
R
SR=C2=(b-a) 2+ab/2×4
=a2+b2-2ab+2ab
=a2+b2
b
a
c
勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
A
B
C
勾
股
弦
归纳:如图,我国古代把直角三角形较短的直角边叫做“勾”,较长的直角边叫做“股”,斜边叫做“弦”.因此,直角三角形三边之间的关系称为勾股定理 .
由前面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a,b,斜边为c,那么一定有a2+b2=c2.
a
A
B
C
b
c
∟
几何语言:
∴a2+b2=c2(勾股定理).
∵在Rt△ABC中 ,∠C=90°,
勾股定理揭示了直角三角形三边之间的关系.
例 1 观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P 的面积为9,正方形Q 的面积为15,则正方形M 的面积为______;
(2)如图②,分别以直角三角形ABC 的
三边长为直径向三角形外作三个半圆,
则这三个半圆形的面积之间的关系式是
.(用图中字母表示)
例题讲解
勾股定理与图形面积
归纳:
与直角三角形三边相连的正方形、半圆及正多边形、圆都具有相同的结论:
两直角边上图形面积的和等于斜边上图形的面积.
本例考查了勾股定理及半圆面积的求法,解答此类题目的关键是仔细观察所给图形,面积与边长、直径有平方关系,就很容易联想到勾股定理.
【跟踪训练】
求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144=x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5
例2 如图,在Rt△ABC中, ∠C=90°.
C
A
B
(1)若a=1,b=2,求c.
(2)若a=15,c=17,求b.
解:
(1)据勾股定理,得
∵c>0
(2)据勾股定理得
∵b>0
【变式题】 在Rt△ABC中,AB=4,AC=3,求BC的长.
4
3
C
A
B
图
4
3
A
C
B
图
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
方法点拨:已知直角三角形的两边求第三边,关键是先明确所求的边是直角边还是斜边,再应用勾股定理.
1.直角三角形ABC的两直角边BC=12,AC=16,则
△ABC的斜边AB的长是 ( )
A.20 B.10 C.9.6 D.8
A
随堂演练
2.下图中,不能用来证明勾股定理的是( )
D
3.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
4.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
5.若直角三角形中,有两边长是5和7,则第三边长的平方为_________.
17
5
74或24
6.已知∠ACB=90°,CD⊥AB,AC=3,BC=4. 求CD的长.
A
D
B
C
3
4
解:因为∠ACB=90°,AC=3,BC=4,
所以AB2=AC2+BC2=25,即AB=5.
根据三角形面积公式,
AC×BC= AB×CD.
所以CD= .
7. 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16;
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.
∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
总结:题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.
课堂小结
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
