苏科版七年级上册数学 6.4平行线复习教案
文档属性
| 名称 | 苏科版七年级上册数学 6.4平行线复习教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 182.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览

文档简介
平行线复习教案
教学目标:
1.复习巩固平行线的条件和性质,使学生会用条件或性质进行简单的推理或计算。
2.使学生所学知识条理化、系统化。
3.使学生进一步熟悉和掌握几何语言及推理证明。
教学重点: 使学生进一步掌握平行线的条件和性质,并能用它们进行简单的推理或计算。
教学难点: 使学生将知识条理化、系统化,能正确地、灵活地运用。
教学过程:
一、课前预习:
1.如图1,在所标识的角中,同位角是( )
A.∠1和∠5 B.∠3和∠5 C.∠4和∠5 D.∠1和∠8
2.已知∠1与∠2是内错角,∠1=40°,则( )
A.∠2=40° B.∠2=140° C.∠2=40°或∠2=140° D.∠2的大小不确定
3.如图2,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
4.如图3,下列条件中,不能判断直线∥的是( ).
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=1800
4.如图,填空
(1)∵∠B=∠1(已知) ∴____//____( )
(2)∵CG // DF(已知) ∴∠2= ( )
(3)∵∠3=∠A(已知) ∴____//____( )
(4)∵AG // DF(已知) ∴∠3=_____( )
(5)∵∠B+∠4=180°(已知) ∴____//____( )
(6)∵CG // DF(已知) ∴∠F+ =180°( )
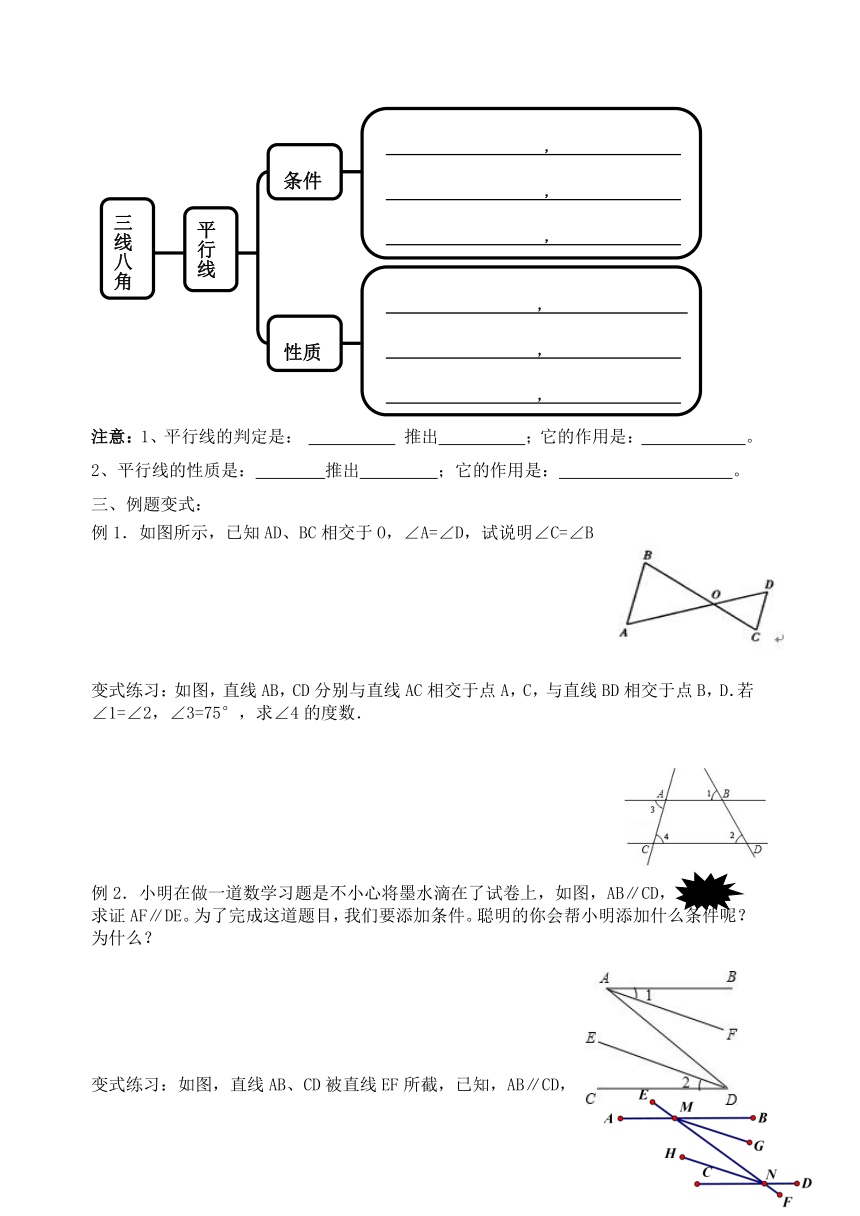
二、知识点梳理
注意:1、平行线的判定是: 推出 ;它的作用是: 。
2、平行线的性质是: 推出 ;它的作用是: 。
三、例题变式:
例1.如图所示,已知AD、BC相交于O,∠A=∠D,试说明∠C=∠B
变式练习:如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
例2.小明在做一道数学习题是不小心将墨水滴在了试卷上,如图,AB∥CD,
求证AF∥DE。为了完成这道题目,我们要添加条件。聪明的你会帮小明添加什么条件呢?为什么?
变式练习:如图,直线AB、CD被直线EF所截,已知,AB∥CD,MG平分∠BMN,NH平分∠CNM.将下列证明MG∥NH的过程及理由填写完整.
证明:∵AB∥CD,(已知)
∴∠BMN =∠CNM,( )
∵MG平分∠BMN,NH平分∠CNM,(已知)
∴∠GMN = ,∠HNM = ,( )
∴ = ,(等量代换)
∴MG∥NH( ).
小结:如果两条平行线被第三条直线所截,那么一对内错角的平分线互相 ;
四、拓展应用:出现转折角,巧作辅助线
例3.已知:如图,AB//CD,∠A=100° ∠C=110°求∠AEC的度数
变式应用:如图,某市二环路修到长虹家电城区时,需拐弯绕城区而过.如果第一次拐的角A是130°,第二次拐的角B是150°,而第三次拐的角是C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C等于( )
A.130° B.140° C.150° D.160°
五、反思小结
六、达标检测
一、选择题
1.如图1,AB∥CD,则与∠1相等的角(∠1除外)共有( )
A.5个 B.4个 C.3个 D.2个
2.如果两条平行线被第三条直线所截,那么一对内错角的平分线互相( ).
A.平行 B.垂直 C.重合 D.不能确定
3.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°D.第一次向左拐50°,第二次向左拐120°
二、填空题
4.如图:已知∠A+∠D=180°,则 ∥ ;已知∠C+∠D=180°,则 ∥ ;理由是 。
5.如图,已知AB∥CD,∠BAE=135°,∠AED =80°,∠EDC的度数是
三、解答题
6.已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
证明:∵ EF⊥AB,CD⊥AB( 已知 )
∴∠FEB= ∠CDB=90°( )
∴ CD∥EF( )
∴ ∠EFB= (两直线平行,同位角相等)
∵ ∠EFB=∠GDC( 已知 )
∴ =∠GDC( )
∴ DG∥BC( )
∴ ∠AGD=∠ACB( )
7.如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
8.如图,直线AB、CD被直线EF所截,已知,AB∥CD,MG平分∠BMN,NH平分∠DNF.证明MG∥NH.提示:(仿照例二的变式完成)
小结:如果两条平行线被第三条直线所截,那么一对同位角的平分线互相 ;
推测:如果两条平行线被第三条直线所截,那么一对同旁内角的平分线互相 。
四、实验探究
9.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜上,被a反射到平面镜b上,又被b镜反射,若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=_____________°,∠3=_____________°;
(2)在(1)中,若∠1=55°,则∠3=_____________°,若∠1=40°,则∠3=_____________°;
(3)由(1)、(2)请你猜想:当两平面镜a、b的夹角∠3=__________°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行,请说明理由.
平行线
三线八角
,
,
,
D
B
条件
性质
,
,
,
C
A
E
C
2
1
B
D
A
E
教学目标:
1.复习巩固平行线的条件和性质,使学生会用条件或性质进行简单的推理或计算。
2.使学生所学知识条理化、系统化。
3.使学生进一步熟悉和掌握几何语言及推理证明。
教学重点: 使学生进一步掌握平行线的条件和性质,并能用它们进行简单的推理或计算。
教学难点: 使学生将知识条理化、系统化,能正确地、灵活地运用。
教学过程:
一、课前预习:
1.如图1,在所标识的角中,同位角是( )
A.∠1和∠5 B.∠3和∠5 C.∠4和∠5 D.∠1和∠8
2.已知∠1与∠2是内错角,∠1=40°,则( )
A.∠2=40° B.∠2=140° C.∠2=40°或∠2=140° D.∠2的大小不确定
3.如图2,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
4.如图3,下列条件中,不能判断直线∥的是( ).
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=1800
4.如图,填空
(1)∵∠B=∠1(已知) ∴____//____( )
(2)∵CG // DF(已知) ∴∠2= ( )
(3)∵∠3=∠A(已知) ∴____//____( )
(4)∵AG // DF(已知) ∴∠3=_____( )
(5)∵∠B+∠4=180°(已知) ∴____//____( )
(6)∵CG // DF(已知) ∴∠F+ =180°( )
二、知识点梳理
注意:1、平行线的判定是: 推出 ;它的作用是: 。
2、平行线的性质是: 推出 ;它的作用是: 。
三、例题变式:
例1.如图所示,已知AD、BC相交于O,∠A=∠D,试说明∠C=∠B
变式练习:如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.
例2.小明在做一道数学习题是不小心将墨水滴在了试卷上,如图,AB∥CD,
求证AF∥DE。为了完成这道题目,我们要添加条件。聪明的你会帮小明添加什么条件呢?为什么?
变式练习:如图,直线AB、CD被直线EF所截,已知,AB∥CD,MG平分∠BMN,NH平分∠CNM.将下列证明MG∥NH的过程及理由填写完整.
证明:∵AB∥CD,(已知)
∴∠BMN =∠CNM,( )
∵MG平分∠BMN,NH平分∠CNM,(已知)
∴∠GMN = ,∠HNM = ,( )
∴ = ,(等量代换)
∴MG∥NH( ).
小结:如果两条平行线被第三条直线所截,那么一对内错角的平分线互相 ;
四、拓展应用:出现转折角,巧作辅助线
例3.已知:如图,AB//CD,∠A=100° ∠C=110°求∠AEC的度数
变式应用:如图,某市二环路修到长虹家电城区时,需拐弯绕城区而过.如果第一次拐的角A是130°,第二次拐的角B是150°,而第三次拐的角是C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C等于( )
A.130° B.140° C.150° D.160°
五、反思小结
六、达标检测
一、选择题
1.如图1,AB∥CD,则与∠1相等的角(∠1除外)共有( )
A.5个 B.4个 C.3个 D.2个
2.如果两条平行线被第三条直线所截,那么一对内错角的平分线互相( ).
A.平行 B.垂直 C.重合 D.不能确定
3.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°D.第一次向左拐50°,第二次向左拐120°
二、填空题
4.如图:已知∠A+∠D=180°,则 ∥ ;已知∠C+∠D=180°,则 ∥ ;理由是 。
5.如图,已知AB∥CD,∠BAE=135°,∠AED =80°,∠EDC的度数是
三、解答题
6.已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
证明:∵ EF⊥AB,CD⊥AB( 已知 )
∴∠FEB= ∠CDB=90°( )
∴ CD∥EF( )
∴ ∠EFB= (两直线平行,同位角相等)
∵ ∠EFB=∠GDC( 已知 )
∴ =∠GDC( )
∴ DG∥BC( )
∴ ∠AGD=∠ACB( )
7.如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
8.如图,直线AB、CD被直线EF所截,已知,AB∥CD,MG平分∠BMN,NH平分∠DNF.证明MG∥NH.提示:(仿照例二的变式完成)
小结:如果两条平行线被第三条直线所截,那么一对同位角的平分线互相 ;
推测:如果两条平行线被第三条直线所截,那么一对同旁内角的平分线互相 。
四、实验探究
9.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜上,被a反射到平面镜b上,又被b镜反射,若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=_____________°,∠3=_____________°;
(2)在(1)中,若∠1=55°,则∠3=_____________°,若∠1=40°,则∠3=_____________°;
(3)由(1)、(2)请你猜想:当两平面镜a、b的夹角∠3=__________°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行,请说明理由.
平行线
三线八角
,
,
,
D
B
条件
性质
,
,
,
C
A
E
C
2
1
B
D
A
E
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
