冀教版数学七年级上册同步课件:2.8 平面图形的旋转(共26张PPT)
文档属性
| 名称 | 冀教版数学七年级上册同步课件:2.8 平面图形的旋转(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 589.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 17:07:53 | ||
图片预览





文档简介
(共26张PPT)
第二章 几何图形的初步认识
2.8 平面图形的旋转
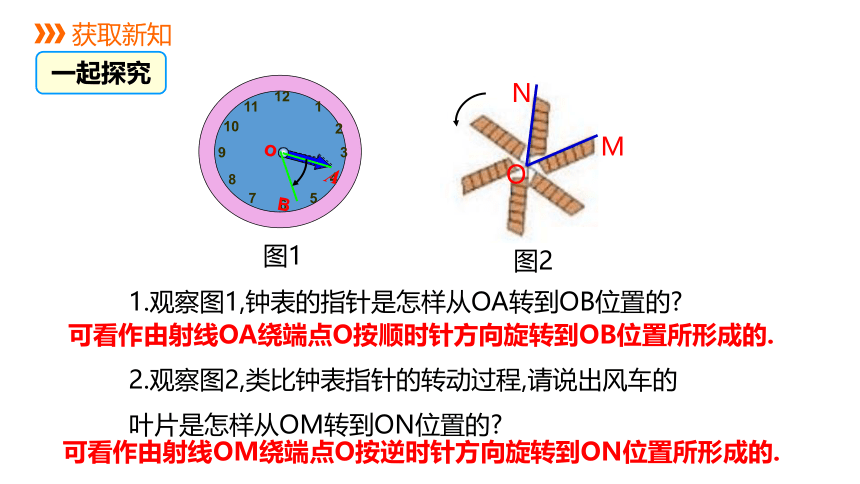
这些运动有什么共同的特点?
情景导入
12
6
1
2
3
4
5
7
8
9
10
11
o
A
B
图1
图2
O
M
N
2.观察图2,类比钟表指针的转动过程,请说出风车的叶片是怎样从OM转到ON位置的
1.观察图1,钟表的指针是怎样从OA转到OB位置的
获取新知
一起探究
可看作由射线OA绕端点O按顺时针方向旋转到OB位置所形成的.
可看作由射线OM绕端点O按逆时针方向旋转到ON位置所形成的.
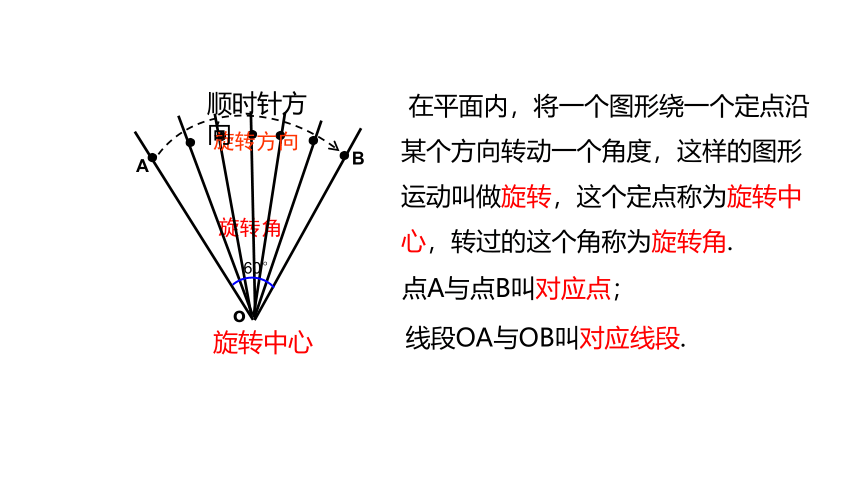
旋转角
旋转中心
A
o
B
.
.
.
.
.
.
.
旋转方向
60°
线段OA与OB叫对应线段.
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心,转过的这个角称为旋转角.
点A与点B叫对应点;
顺时针方向
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
温馨提示:旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度”称之为旋转的三要素.
旋转的性质
A
B
B′
A′
C
.
M′
M
.
.
.
.
45°
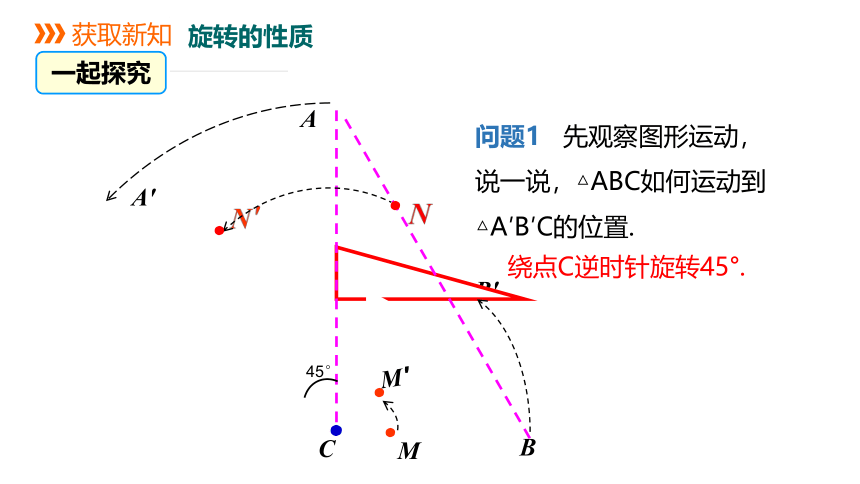
问题1 先观察图形运动,说一说,△ABC如何运动到△A′B′C的位置.
绕点C逆时针旋转45°.
获取新知
一起探究
旋转中心是点__________;
图中对应点有_______________________________________;
图中对应线段有_____________________________________.
每对对应线段的长度有怎样的关系?
图中旋转角等于________.
C
点A与点A′,点B与点B′,点M与点M′,点N与点N′
线段CA与CA′、CB与CB′、AB与A′B′
45°
相等
根据上图填空.
B'
A'
C'
A
B
C
O
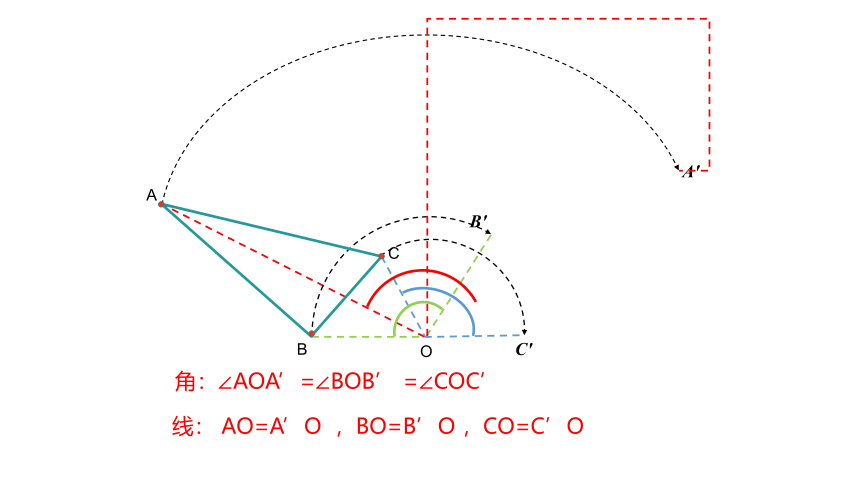
线: AO=A’O ,BO=B’O ,CO=C’O
角:∠AOA’=∠BOB’ =∠COC’
旋转中心、旋转角
归 纳:
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
问题1 如图,已知A,B是射线OM上的两点,且OA=1cm,OB=2.5cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点 A′,B′,的位置,请画出点 A′,B′.
A′
B′
一起探究
A′
B′
(2) OA和OA′ ,OB和OB′ 分别有怎样的数量关系?
OA=OA′ ,OB=OB′
问题2 如图,三角形AOB绕点O按顺时针方向旋转后得到三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD都相等吗?
相等
(2)∠BOD与∠AOC相等吗?
相等
(3)画出点E的对应点F.
方法一:用圆规以C点为圆心,以线段AE长
为半径画弧,与CD交于点F.
方法二:用圆规以D为圆心,以线段BE长为
半径画弧,与CD交于点F.
方法三:根据旋转角,通过射线旋转作出点F.
旋转的性质
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
对应点到旋转中心的距离相等;
每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
B'
B
A
已知线段AB请利用三角板刻度尺或量角器等工具,画出线段AB绕点A、逆时针、旋转90°后的图形AB′.
90°
想一想:若再加上一个点M,与A、B连成△ABM ,你能做出它绕点A逆时针旋转90°后的△AB′M′吗?试着做一做.
M
C
D
M'
一起探究
旋转作图的步骤:
(1)确定旋转中心、旋转方向及旋转角的大小;
(2)确定已知图形的关键点(比如线段的两个端点、三角形的三个顶点等);
(3)确定各关键点的对应点.(将图形的各关键点与旋转中心连接,按规定方向旋转规定角度,找到该点的对应点);
(4)按原图顶点的顺序连接各对应点,即得旋转后的图形.
1.下列现象中,属于旋转的是( )
A.钟摆的摆动 B.飞机在飞行
C.汽车在奔驰 D.小鸟飞翔
A
随堂演练
2.如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
3.如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是 ( )
A.45°
B.60°
C.90°
D.120°
B
4.如图,把三角形ABC绕点O按顺时针方向旋转一定角度后成为三角形A′B′C′,则下列各式:①AB=A′B′;②OB=OB′;③∠AOA′=∠COC′;④∠COB=∠A′OC′;⑤∠COA′=∠BOC′.其中,成立的有( )
A.2个
B.3个
C.4个
D.5个
B
5.如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60°
B.105°
C.120°
D.135°
B
6.填空
(1) 图形1绕点O顺时针旋转90°到图形( )的所在位置;
(2)图形2绕点O顺时针旋转90°到图形( )的所在位置;
(3)图形2绕点O顺时针旋转( )到图形4的位置.
2
3
180°
7.如图,将三角形ABC绕点C按逆时针方向旋转25°得到三角形DEC,已知∠A=25°,∠ACE=80°,则∠B=________.
50°
8.将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是___________.
120°
9.在下图中,将大写字母 N 绕它下侧的顶点按顺时针方向旋转 90 ,作出旋转后的图案.
平面图形的旋转
旋转的定义
旋转的性质
在平面内,把一个图形绕某一个定点转动一个角度的图形变换称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
1.旋转不改变图形的大小与形状,但可改变方向.
2.对应点到旋转中心的距离相等
3.旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是相等的角,它们都等于旋转角,
课堂小结
第二章 几何图形的初步认识
2.8 平面图形的旋转
这些运动有什么共同的特点?
情景导入
12
6
1
2
3
4
5
7
8
9
10
11
o
A
B
图1
图2
O
M
N
2.观察图2,类比钟表指针的转动过程,请说出风车的叶片是怎样从OM转到ON位置的
1.观察图1,钟表的指针是怎样从OA转到OB位置的
获取新知
一起探究
可看作由射线OA绕端点O按顺时针方向旋转到OB位置所形成的.
可看作由射线OM绕端点O按逆时针方向旋转到ON位置所形成的.
旋转角
旋转中心
A
o
B
.
.
.
.
.
.
.
旋转方向
60°
线段OA与OB叫对应线段.
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心,转过的这个角称为旋转角.
点A与点B叫对应点;
顺时针方向
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
温馨提示:旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度”称之为旋转的三要素.
旋转的性质
A
B
B′
A′
C
.
M′
M
.
.
.
.
45°
问题1 先观察图形运动,说一说,△ABC如何运动到△A′B′C的位置.
绕点C逆时针旋转45°.
获取新知
一起探究
旋转中心是点__________;
图中对应点有_______________________________________;
图中对应线段有_____________________________________.
每对对应线段的长度有怎样的关系?
图中旋转角等于________.
C
点A与点A′,点B与点B′,点M与点M′,点N与点N′
线段CA与CA′、CB与CB′、AB与A′B′
45°
相等
根据上图填空.
B'
A'
C'
A
B
C
O
线: AO=A’O ,BO=B’O ,CO=C’O
角:∠AOA’=∠BOB’ =∠COC’
旋转中心、旋转角
归 纳:
一个图形由一个位置旋转到另一个位置,固定不动的点就是旋转中心,互换位置的点是对应点,互换位置的边是对应边,对应边的夹角是旋转角.
问题1 如图,已知A,B是射线OM上的两点,且OA=1cm,OB=2.5cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点 A′,B′,的位置,请画出点 A′,B′.
A′
B′
一起探究
A′
B′
(2) OA和OA′ ,OB和OB′ 分别有怎样的数量关系?
OA=OA′ ,OB=OB′
问题2 如图,三角形AOB绕点O按顺时针方向旋转后得到三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD都相等吗?
相等
(2)∠BOD与∠AOC相等吗?
相等
(3)画出点E的对应点F.
方法一:用圆规以C点为圆心,以线段AE长
为半径画弧,与CD交于点F.
方法二:用圆规以D为圆心,以线段BE长为
半径画弧,与CD交于点F.
方法三:根据旋转角,通过射线旋转作出点F.
旋转的性质
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
对应点到旋转中心的距离相等;
每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
B'
B
A
已知线段AB请利用三角板刻度尺或量角器等工具,画出线段AB绕点A、逆时针、旋转90°后的图形AB′.
90°
想一想:若再加上一个点M,与A、B连成△ABM ,你能做出它绕点A逆时针旋转90°后的△AB′M′吗?试着做一做.
M
C
D
M'
一起探究
旋转作图的步骤:
(1)确定旋转中心、旋转方向及旋转角的大小;
(2)确定已知图形的关键点(比如线段的两个端点、三角形的三个顶点等);
(3)确定各关键点的对应点.(将图形的各关键点与旋转中心连接,按规定方向旋转规定角度,找到该点的对应点);
(4)按原图顶点的顺序连接各对应点,即得旋转后的图形.
1.下列现象中,属于旋转的是( )
A.钟摆的摆动 B.飞机在飞行
C.汽车在奔驰 D.小鸟飞翔
A
随堂演练
2.如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
3.如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是 ( )
A.45°
B.60°
C.90°
D.120°
B
4.如图,把三角形ABC绕点O按顺时针方向旋转一定角度后成为三角形A′B′C′,则下列各式:①AB=A′B′;②OB=OB′;③∠AOA′=∠COC′;④∠COB=∠A′OC′;⑤∠COA′=∠BOC′.其中,成立的有( )
A.2个
B.3个
C.4个
D.5个
B
5.如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60°
B.105°
C.120°
D.135°
B
6.填空
(1) 图形1绕点O顺时针旋转90°到图形( )的所在位置;
(2)图形2绕点O顺时针旋转90°到图形( )的所在位置;
(3)图形2绕点O顺时针旋转( )到图形4的位置.
2
3
180°
7.如图,将三角形ABC绕点C按逆时针方向旋转25°得到三角形DEC,已知∠A=25°,∠ACE=80°,则∠B=________.
50°
8.将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是___________.
120°
9.在下图中,将大写字母 N 绕它下侧的顶点按顺时针方向旋转 90 ,作出旋转后的图案.
平面图形的旋转
旋转的定义
旋转的性质
在平面内,把一个图形绕某一个定点转动一个角度的图形变换称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
1.旋转不改变图形的大小与形状,但可改变方向.
2.对应点到旋转中心的距离相等
3.旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是相等的角,它们都等于旋转角,
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
