冀教版数学七年级上册同步课件:3.2 第3课时 列代数式(2)(共20张PPT)
文档属性
| 名称 | 冀教版数学七年级上册同步课件:3.2 第3课时 列代数式(2)(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 640.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 17:12:34 | ||
图片预览








文档简介
(共20张PPT)
第二章 代数式
3.2 第3课时 列代数式(2)
已知甲、乙、丙三个数的比为1:2:3.如果设甲数为x,请表示出甲、乙两数的和减去丙数后的差;如果设丙数为z,请表示出甲、丙两数的和减去乙数后的差.
知识回顾
复习
问题1 一个两位数,个位上的数字是a,十位上的数字是b,把十位上的数字与个位上的数字对调后,得到一个新数.用式子分别表示这两个数及它们的和.
分析:用字母表示多位数,可以先画出数位图.
10b+a
10a+b
两数之和即为:(10b+a)+(10a+b)
用代数式表示较复杂的数量关系
获取新知
一起探究
问题2 经过练习,小亮和大华的打字速度都有了提高,小亮的打字速度达到80个/分,大华比小亮每分钟多打10个字.
(1)小亮和大华a min分别能打多少个字?
(2)b min大华比小亮多打多少个字?
(3)将同为c个字的两篇文章分别给小亮和大华打,如果要求他们同时完成任务,那么小亮比大华要提前多少分钟开始打字?
问题思考:
(1)问题中涉及三个基本的量是什么?
打字速度、时间、打字的个数
(2)这三个量之间具有怎样的关系?
打字的个数=打字速度×时间
(3)小亮和大华a min分别能打多少个字?
小亮打字80a个;大华打字90a个
(4)b min大华比小亮多打多少个字?
10b个
(5)将同为c个字的两篇文章分别交给小亮和大华打,如果要求他们同时完成任务,那么小亮比大华要提前多少分钟开始打字?
解:(1)小亮a min打的字数为:80a个;大华a min打的字数为(80+10)a个,即90a个.
(2)大华每分钟比小亮多打10个字,则大华b min比小亮多打10b个字.
(3)打完c个字,小亮所需时间为: min 大华所需时间为 min.小亮需提前 min.
列代数式表示较为复杂的实际问题时,需认真审题,弄清问题中各数量之间的关系和运算顺序,即必须把实际情境中数量关系分析清楚,然后按照代数式书写格式的规范进行书写.
归 纳
例1:从A 地乘火车到北京,普通票价格为40元/人,学生票价格为20元/人.星期日,A 地育才学校组织部分师生到天安门广场观看升旗仪式.
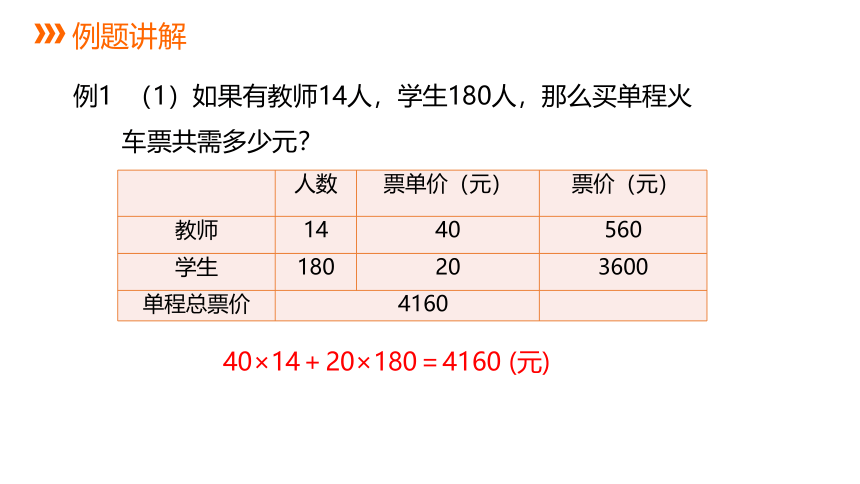
(1)如果有教师14人,学生180人,那么买单程火车票共需多少元?
(2)如果有教师x人,学生y人,那么买单程火车票共需多少元?
(3)如果教师人数恰好是学生人数的 ,将教师的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
例题讲解
例题讲解
例1 (1)如果有教师14人,学生180人,那么买单程火车票共需多少元?
40×14+20×180=4160 (元)
人数 票单价(元) 票价(元)
教师 14 40 560
学生 180 20 3600
单程总票价 4160
人数 票单价/元 票价/元
教师 x 40
学生 y 20
单程总票价 40 x
20 y
40x+20y
(2)如果有教师x人,学生y人,那么买单程火车票共需多少元?
(40x+20y)元
人数 票单价(元) 票价(元)
教师 x 40
学生 20
单程总票价 如果设教师有x人,那么学生有12x人,
(3)如果教师人数恰好是学生人数的 ,将教师 的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
40 x
40x+20×12x
20×12x
12x
则买单程车票共需(40x+20×12x)元.
人数 票单价(元) 票价(元)
教师 40
学生 y 20
单程总票价 (3)如果教师人数恰好是学生人数的 ,将教师 的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
20y
如果设学生有y人,那么教师有 人,
则买单程车票共需 元,即 元.
例2: 你能帮代数式10x+5y找一些现实生活中的实际情景吗?并解释它表示什么.
解释一:火龙果每千克x元,番石榴每千克y元,买10千克火龙果与5千克番石榴共花 元.
(10x+5y)
解释二:火龙果每千克10元,番石榴每千克5元,买x千克火龙果与y千克番石榴共花 元.
(10x+5y)
例题讲解
1.三个相邻的奇数,中间的一个为m,则较小的一个为_______,较大的一个为_________.
2.a是一个两位数,已知十位数字为b,则个位数字是 ,交换个位、十位上的数字后,所得的新的两位数是__________ .
随堂演练
3.如果某船行驶第1千米的运费是25元,以后每增加1千米,运费增加5元,现在某人租船要行驶s千米(s为整数,s≥1),所需运费表示为_______________.
元
4.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元.则代数式500-3a-2b表示的数为
解析:因为买一个足球a元,一个篮球b元,所以3a表示体育委员买了3个足球,2b表示买了2个篮球,所以代数式500﹣3a﹣2b:表示体育委员买了3个足球、2个篮球,剩余的钱.
体育委员买了3个足球、2个篮球,剩余的钱
5.甲、乙两品牌上衣的单价分别为x元、 y元。在换季时,甲品牌上衣按4折(即原价的40%)销售,乙品牌上衣按6折销售。这时购买两种品牌的上衣各一件,共需多少元?
解 : 40%x+60%y
答:购买两种品牌的上衣各一件,共需(40%x+60%y)元.
6.某公司在甲、乙两个仓库分别用农用车12辆和6辆,现需要调往A县10辆,调往B县8辆.已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元,从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
设从甲仓库调往A县农用车x辆.
⑴甲仓库调往B县农用车_____ 辆,乙仓库调往A
县农用车______ 辆.(用含x的代数式表示);
(12-x)
(10-x)
⑵写出公司从甲、乙两个仓库调往农用车到A、B两县所需要的总运费.(用含x的代数式表示).
到A县的总费用=40x+30(10-x)元
到B县的总费用=80(12-x)+50(x-4)元
3.熟悉相关知识,正确使用括号;
4.若用“和”“总“表示后式子后面有单位,式子要放到括号内.
用代数式表示实际问题中的数量关系时,必须注意以下四点:
1.抓住关键词语,确定所求问题与已知条件之间的数量关系;
2.理清问题中的语句的层次,明确运算顺序;
课堂小结
第二章 代数式
3.2 第3课时 列代数式(2)
已知甲、乙、丙三个数的比为1:2:3.如果设甲数为x,请表示出甲、乙两数的和减去丙数后的差;如果设丙数为z,请表示出甲、丙两数的和减去乙数后的差.
知识回顾
复习
问题1 一个两位数,个位上的数字是a,十位上的数字是b,把十位上的数字与个位上的数字对调后,得到一个新数.用式子分别表示这两个数及它们的和.
分析:用字母表示多位数,可以先画出数位图.
10b+a
10a+b
两数之和即为:(10b+a)+(10a+b)
用代数式表示较复杂的数量关系
获取新知
一起探究
问题2 经过练习,小亮和大华的打字速度都有了提高,小亮的打字速度达到80个/分,大华比小亮每分钟多打10个字.
(1)小亮和大华a min分别能打多少个字?
(2)b min大华比小亮多打多少个字?
(3)将同为c个字的两篇文章分别给小亮和大华打,如果要求他们同时完成任务,那么小亮比大华要提前多少分钟开始打字?
问题思考:
(1)问题中涉及三个基本的量是什么?
打字速度、时间、打字的个数
(2)这三个量之间具有怎样的关系?
打字的个数=打字速度×时间
(3)小亮和大华a min分别能打多少个字?
小亮打字80a个;大华打字90a个
(4)b min大华比小亮多打多少个字?
10b个
(5)将同为c个字的两篇文章分别交给小亮和大华打,如果要求他们同时完成任务,那么小亮比大华要提前多少分钟开始打字?
解:(1)小亮a min打的字数为:80a个;大华a min打的字数为(80+10)a个,即90a个.
(2)大华每分钟比小亮多打10个字,则大华b min比小亮多打10b个字.
(3)打完c个字,小亮所需时间为: min 大华所需时间为 min.小亮需提前 min.
列代数式表示较为复杂的实际问题时,需认真审题,弄清问题中各数量之间的关系和运算顺序,即必须把实际情境中数量关系分析清楚,然后按照代数式书写格式的规范进行书写.
归 纳
例1:从A 地乘火车到北京,普通票价格为40元/人,学生票价格为20元/人.星期日,A 地育才学校组织部分师生到天安门广场观看升旗仪式.
(1)如果有教师14人,学生180人,那么买单程火车票共需多少元?
(2)如果有教师x人,学生y人,那么买单程火车票共需多少元?
(3)如果教师人数恰好是学生人数的 ,将教师的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
例题讲解
例题讲解
例1 (1)如果有教师14人,学生180人,那么买单程火车票共需多少元?
40×14+20×180=4160 (元)
人数 票单价(元) 票价(元)
教师 14 40 560
学生 180 20 3600
单程总票价 4160
人数 票单价/元 票价/元
教师 x 40
学生 y 20
单程总票价 40 x
20 y
40x+20y
(2)如果有教师x人,学生y人,那么买单程火车票共需多少元?
(40x+20y)元
人数 票单价(元) 票价(元)
教师 x 40
学生 20
单程总票价 如果设教师有x人,那么学生有12x人,
(3)如果教师人数恰好是学生人数的 ,将教师 的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
40 x
40x+20×12x
20×12x
12x
则买单程车票共需(40x+20×12x)元.
人数 票单价(元) 票价(元)
教师 40
学生 y 20
单程总票价 (3)如果教师人数恰好是学生人数的 ,将教师 的人数或学生的人数用字母表示,那么买单程火车票共需要多少元?
20y
如果设学生有y人,那么教师有 人,
则买单程车票共需 元,即 元.
例2: 你能帮代数式10x+5y找一些现实生活中的实际情景吗?并解释它表示什么.
解释一:火龙果每千克x元,番石榴每千克y元,买10千克火龙果与5千克番石榴共花 元.
(10x+5y)
解释二:火龙果每千克10元,番石榴每千克5元,买x千克火龙果与y千克番石榴共花 元.
(10x+5y)
例题讲解
1.三个相邻的奇数,中间的一个为m,则较小的一个为_______,较大的一个为_________.
2.a是一个两位数,已知十位数字为b,则个位数字是 ,交换个位、十位上的数字后,所得的新的两位数是__________ .
随堂演练
3.如果某船行驶第1千米的运费是25元,以后每增加1千米,运费增加5元,现在某人租船要行驶s千米(s为整数,s≥1),所需运费表示为_______________.
元
4.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元.则代数式500-3a-2b表示的数为
解析:因为买一个足球a元,一个篮球b元,所以3a表示体育委员买了3个足球,2b表示买了2个篮球,所以代数式500﹣3a﹣2b:表示体育委员买了3个足球、2个篮球,剩余的钱.
体育委员买了3个足球、2个篮球,剩余的钱
5.甲、乙两品牌上衣的单价分别为x元、 y元。在换季时,甲品牌上衣按4折(即原价的40%)销售,乙品牌上衣按6折销售。这时购买两种品牌的上衣各一件,共需多少元?
解 : 40%x+60%y
答:购买两种品牌的上衣各一件,共需(40%x+60%y)元.
6.某公司在甲、乙两个仓库分别用农用车12辆和6辆,现需要调往A县10辆,调往B县8辆.已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元,从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
设从甲仓库调往A县农用车x辆.
⑴甲仓库调往B县农用车_____ 辆,乙仓库调往A
县农用车______ 辆.(用含x的代数式表示);
(12-x)
(10-x)
⑵写出公司从甲、乙两个仓库调往农用车到A、B两县所需要的总运费.(用含x的代数式表示).
到A县的总费用=40x+30(10-x)元
到B县的总费用=80(12-x)+50(x-4)元
3.熟悉相关知识,正确使用括号;
4.若用“和”“总“表示后式子后面有单位,式子要放到括号内.
用代数式表示实际问题中的数量关系时,必须注意以下四点:
1.抓住关键词语,确定所求问题与已知条件之间的数量关系;
2.理清问题中的语句的层次,明确运算顺序;
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
