冀教版数学七年级上册同步课件:3.2 第1课时 代数式(共16张PPT)
文档属性
| 名称 | 冀教版数学七年级上册同步课件:3.2 第1课时 代数式(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第三章 代数式
3.2 第1课时 代数式的概念及意义
我们小时候都听过这样一段儿歌
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水……”请接下去.
n只青蛙, 张嘴, 只眼睛,
条腿, 声扑通跳下水.
n
2n
4n
n
情景导入
代数式的概念
用含有字母的式子表示下列数量关系:
(1)买一个足球需要a元,买一个篮球需要b元,则买一个足球和一个篮球共需要___________ 元;
(2)某产品前年的产量是n件,去年的产量是前年产量的3倍少20件,去年的产量是___________ 件;
(3)某一正方形菜地的边长为am,它的面积是另一菜地面积的2倍,另一菜地的面积为___________ m2 .
获取新知
代数式的概念
定 义:
在上述例子中,出现了a+b,3n-20, 等,像这样用运算符号连接数和字母组成的式子叫做代数式.(运算符号包括+、-、×、÷、乘方)
1.单独的一个数或一个表示数的字母也叫代数式.
2.代数式中除了含有数,字母和运算符号外,还可以含有括号.
3.代数中不含有“=”、“>”、“<”.
【注意】
下列式子中,哪些是代数式?
(1)x+6;(2)x=2x-1;(3)a;(4)2n>3;(5)0.
注意:代数式中的式是指由+、-、×、÷、乘方运算符号连接而成的式子.
解: ∵代数式不能含有“=”“>”或“<”,
∴是代数式的有:(1)(3)(5).
练一练
1.字母与字母,数或字母与括号相乘时,“×” 号通常省略不写或写成“·”;
代数式的书写规则:
2.数与字母相乘时,数字通常写在字母的左边,数字与数字相乘时,仍用“×” 号,也可用“·”号,但要注意与小数点区分开;
100×t
100t或100·t
b×2a
2ab或2·a·b
知识要点
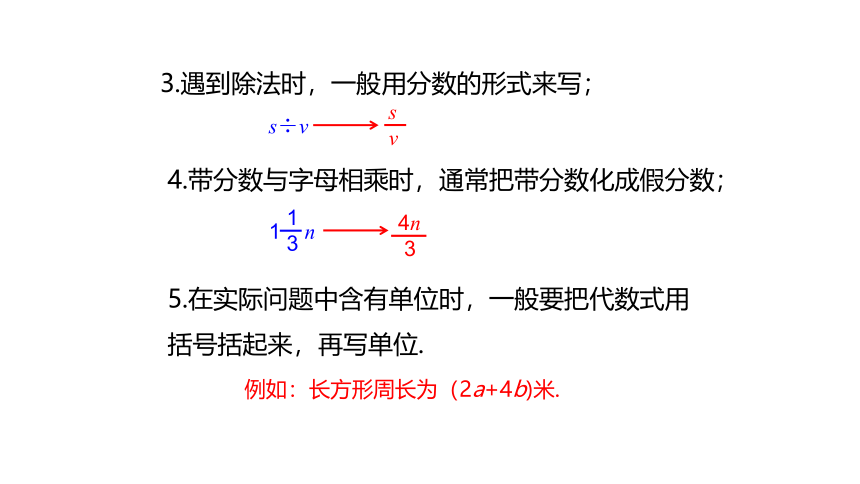
3.遇到除法时,一般用分数的形式来写;
4.带分数与字母相乘时,通常把带分数化成假分数;
5.在实际问题中含有单位时,一般要把代数式用括号括起来,再写单位.
1
3
1 n
4n
3
s÷v
s
v
例如:长方形周长为(2a+4b)米.
判断下列式子书写是否规范,不规范的请改正.
做一做
解:(1)2a+5表示的是a的2倍与5的和.
(2)2(a+5)表示的是a与5的和的2倍.
(3)a2+b2表示的是a的平方与b的平方的和.
(4)(a+b)2表示的是a与b的和的平方.
例1 指出下列各代数式的意义:
(1)2a+5; (2)2(a+5);(3)a2+b2; (4)(a+b)2.
例题讲解
给你一段文字语言,能不能写出表示它的代数式?用代数式表示“a,8”两数之和与b,c两数之差的积.
a
8
两数的和
a+8
b
c
两数的差
b-c
两数
的积
(a+8)(b-c)
例2 用代数式表示:
(1)a与b的差与c的平方的和.
(2)百位数字是a,十位数字是b,个位数字是c的三位数.
(3)三个连续的的整数(用同一个字母表示),以及它们的和.
解:(1)(a-b)+ c2.
(2)100a+10b+ c.(其中a,b,c是0到9之间的整数,且a≠0.
(3)设m是正数,三个连续整数可表示为m-1,m,m+1,它们的和为(m-1)+m+(m+1).
例题讲解
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序,一般按“先读先写”的原则列出式子.
③牢记一些概念和公式.
归 纳
1.用代数式表示:
(1)一个数x与6的和;
(2)比-5小a的数;
(3)某校买书25本,每本a元,该校应付书费多少元?
(4)容量为60L的铁桶,贮满油,取出(x+1)L后,桶内还剩油多少升?
解:
(1) x+6;
(2) -5-a;
(3) 25a元;
(4)[60-(x+1)]L.
随堂演练
解:
(1) m、n两数的平方差;
(2) x、y两数的和与它们的差的乘积的7倍;
(3) a、b两数的和除以它们的差的商;
(4) x的平方的2倍与y的平方的3倍的差.
2.用语言叙述下列代数式:
(1) ;
(2) ;
(3) ;
(4) .
3.3月12日(植树节)学校团委组织260名学生(其中女生b人)去市青少年世纪林植树,每个男生植树x棵,每个女生植树y棵.你能用代数式表示他们共植树多少棵吗?
解:因为女生为b人,所以男生有 人.
根据题意,男生共植树 ,女生共
植树by棵.
(260-b)
(260-b)x
所以他们共植树[(260-b)x+by]棵.
代数式
定义
应用
用运算符号连接数和字母组成的式子叫做代数式.单独的一个数或字母也是代数式.
代数式所表示的意义
根据实际问题列代数式
课堂小结
第三章 代数式
3.2 第1课时 代数式的概念及意义
我们小时候都听过这样一段儿歌
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水……”请接下去.
n只青蛙, 张嘴, 只眼睛,
条腿, 声扑通跳下水.
n
2n
4n
n
情景导入
代数式的概念
用含有字母的式子表示下列数量关系:
(1)买一个足球需要a元,买一个篮球需要b元,则买一个足球和一个篮球共需要___________ 元;
(2)某产品前年的产量是n件,去年的产量是前年产量的3倍少20件,去年的产量是___________ 件;
(3)某一正方形菜地的边长为am,它的面积是另一菜地面积的2倍,另一菜地的面积为___________ m2 .
获取新知
代数式的概念
定 义:
在上述例子中,出现了a+b,3n-20, 等,像这样用运算符号连接数和字母组成的式子叫做代数式.(运算符号包括+、-、×、÷、乘方)
1.单独的一个数或一个表示数的字母也叫代数式.
2.代数式中除了含有数,字母和运算符号外,还可以含有括号.
3.代数中不含有“=”、“>”、“<”.
【注意】
下列式子中,哪些是代数式?
(1)x+6;(2)x=2x-1;(3)a;(4)2n>3;(5)0.
注意:代数式中的式是指由+、-、×、÷、乘方运算符号连接而成的式子.
解: ∵代数式不能含有“=”“>”或“<”,
∴是代数式的有:(1)(3)(5).
练一练
1.字母与字母,数或字母与括号相乘时,“×” 号通常省略不写或写成“·”;
代数式的书写规则:
2.数与字母相乘时,数字通常写在字母的左边,数字与数字相乘时,仍用“×” 号,也可用“·”号,但要注意与小数点区分开;
100×t
100t或100·t
b×2a
2ab或2·a·b
知识要点
3.遇到除法时,一般用分数的形式来写;
4.带分数与字母相乘时,通常把带分数化成假分数;
5.在实际问题中含有单位时,一般要把代数式用括号括起来,再写单位.
1
3
1 n
4n
3
s÷v
s
v
例如:长方形周长为(2a+4b)米.
判断下列式子书写是否规范,不规范的请改正.
做一做
解:(1)2a+5表示的是a的2倍与5的和.
(2)2(a+5)表示的是a与5的和的2倍.
(3)a2+b2表示的是a的平方与b的平方的和.
(4)(a+b)2表示的是a与b的和的平方.
例1 指出下列各代数式的意义:
(1)2a+5; (2)2(a+5);(3)a2+b2; (4)(a+b)2.
例题讲解
给你一段文字语言,能不能写出表示它的代数式?用代数式表示“a,8”两数之和与b,c两数之差的积.
a
8
两数的和
a+8
b
c
两数的差
b-c
两数
的积
(a+8)(b-c)
例2 用代数式表示:
(1)a与b的差与c的平方的和.
(2)百位数字是a,十位数字是b,个位数字是c的三位数.
(3)三个连续的的整数(用同一个字母表示),以及它们的和.
解:(1)(a-b)+ c2.
(2)100a+10b+ c.(其中a,b,c是0到9之间的整数,且a≠0.
(3)设m是正数,三个连续整数可表示为m-1,m,m+1,它们的和为(m-1)+m+(m+1).
例题讲解
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序,一般按“先读先写”的原则列出式子.
③牢记一些概念和公式.
归 纳
1.用代数式表示:
(1)一个数x与6的和;
(2)比-5小a的数;
(3)某校买书25本,每本a元,该校应付书费多少元?
(4)容量为60L的铁桶,贮满油,取出(x+1)L后,桶内还剩油多少升?
解:
(1) x+6;
(2) -5-a;
(3) 25a元;
(4)[60-(x+1)]L.
随堂演练
解:
(1) m、n两数的平方差;
(2) x、y两数的和与它们的差的乘积的7倍;
(3) a、b两数的和除以它们的差的商;
(4) x的平方的2倍与y的平方的3倍的差.
2.用语言叙述下列代数式:
(1) ;
(2) ;
(3) ;
(4) .
3.3月12日(植树节)学校团委组织260名学生(其中女生b人)去市青少年世纪林植树,每个男生植树x棵,每个女生植树y棵.你能用代数式表示他们共植树多少棵吗?
解:因为女生为b人,所以男生有 人.
根据题意,男生共植树 ,女生共
植树by棵.
(260-b)
(260-b)x
所以他们共植树[(260-b)x+by]棵.
代数式
定义
应用
用运算符号连接数和字母组成的式子叫做代数式.单独的一个数或字母也是代数式.
代数式所表示的意义
根据实际问题列代数式
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
