冀教版数学七年级上册同步课件:3.3 第1课时 代数式的值(共21张PPT)
文档属性
| 名称 | 冀教版数学七年级上册同步课件:3.3 第1课时 代数式的值(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 17:15:56 | ||
图片预览






文档简介
(共21张PPT)
第三章 代数式
3.3 第1课时 代数式的值
情景导入
...
...
...
...
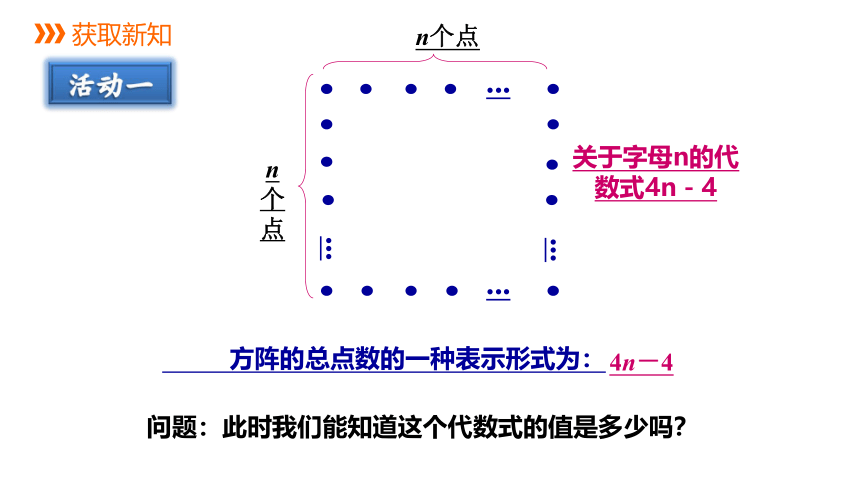
方阵的总点数的一种表示形式为:
n个点
n个点
关于字母n的代数式4n-4
4n-4
问题:此时我们能知道这个代数式的值是多少吗?
获取新知
(1)当n取4, 10, 13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值.
n=4时,4×4-4=12
n=10时,4×10-4=36
n=13时,4×13-4=48
n=25时,4×25-4=96
思考:
(2)对于n的同一个值,同学们得到的结果都相同吗?
相同
(3)总结:从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代数式相应的值.一个代数式,可以看做一个计算程序.
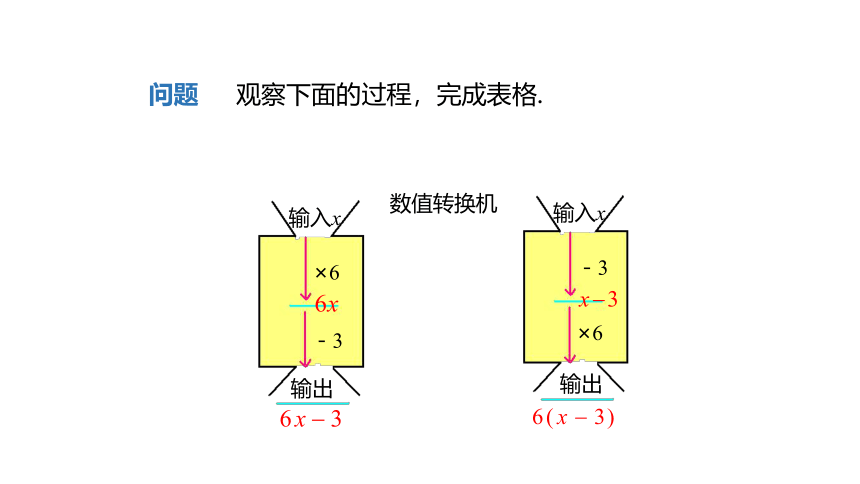
数值转换机
输入x
输入x
输出
输出
×6
-3
×6
-3
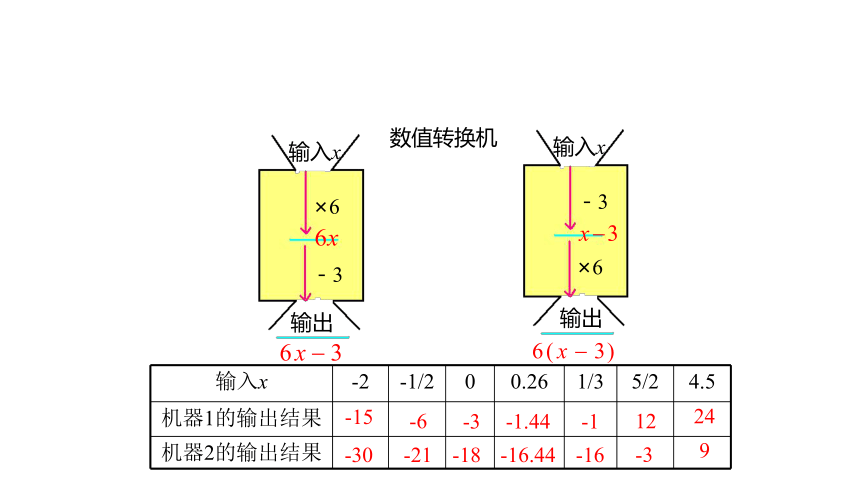
问题 观察下面的过程,完成表格.
数值转换机
输入x
输入x
输出
输出
×6
-3
×6
-3
输入x -2 -1/2 0 0.26 1/3 5/2 4.5
机器1的输出结果
机器2的输出结果
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
定 义:
像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值.这个过程叫做求代数式的值.
求代数式的值的概念
求下列代数式的值时,代入过程正确的是( )
1.当 时,
2.当 时,
3.当 时,
4.当 时,
4
活动二
(1)代入时,要“对号入座”,避免代错字母,其他符号不变;
(2)代数式中,代入数值以后原来省略的乘号一定要还原;
(3)若字母的值是负数或分数,将字母的值代入代数式时,应加上括号,原来的数字和运算符号都不能改变.
在代入数值时应注意
例1 根据下面a,b的值,求代数式 的值
(1)a=2,b=-6;
例题讲解
写出条件:当……时
抄写代数式
代入数值
计算
例1 根据下面a,b的值,求代数式 的值
(2)a=-10,b=4
例2 如图,已知长方体的高为h,底面是边长为a的正方形.当h=3,a=2时,分别求其体积V和表面积S.
解:因为V=a2h,S=2a2+4ah,
所以 当h=3,a=2时,
V=a2h=22×3=12,
S=2a2+4ah=2×22+4×2×3=32.
拓展 整体代入法求代数式的值
例3 已知x+y=5,xy=2,求代数式(x+y)2-5xy的值.
解:因为x+y=5,xy=2,
所以(x+y)2-5xy=52-5×2=25-10=15.
相同的代数式可以看作一个字母——整体代入
随堂演练
1. 下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.平行四边形具有的性质矩形都具有
B
1.当x=1时,代数式4-3x的值是( )
A.1 B.2 C.3 D.4
2.若 则x2-y3的值为( )
A.1 B.-1 C. D.2
3.如果2a+3b=5,那么4a+6b-7= .
已知a+b=5,ab=6 ,则ab-(a+b)=___.
A
C
3
1
4.根据下面a,b的值,求代数式a2-2ab-b2 和(a-b)2 的值:
(1)a= ,b=3; (2)a=5,b=3.
(2)当a=5,b=3时,a2-2ab-b2=52-2×5×3+32=25-30+9=4.
(a-b)2 =(5-3)2 =4.
(1)当a= ,b=3时,
解:
通过计算结果你发现了什么?
5.某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
(2)把x=37,y=15代入代数式,得
10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
(1)该旅游团应付的门票费是(10x+5y)元.
解:
6.某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 优惠办法
少于200元 不予优惠
低于500元但 不低于200元 九折优惠
500元或超过500元 其中500元部分给予九折优惠,
超过500元部分给予八折优惠
(1)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他应付款________元,当x大于或等于500元时,他应付款____________元(用含x的代数式表示);
(2)王老师一次性购物600元,他实际付款________元;
(3)王老师第一次购物用了170元,第二次购物用了387元,如果王老师将这两次的购物换作一次购买可以节省________元.
解: (1)0.9x;500×0.9+(x-500)×0.8;
(2) 500×0.9+(600-500)×0.8=530;
(3)200×0.9=180,500×0.9=450,
所以设第二次购物原价为x,则0.9x=387,x=430,两次购物的原价是170+430=600(元),所以如果一次购买只需530元,节省27元.
代数式的值
代数式的值
利用代数式的值解决实际问题
课堂小结
第三章 代数式
3.3 第1课时 代数式的值
情景导入
...
...
...
...
方阵的总点数的一种表示形式为:
n个点
n个点
关于字母n的代数式4n-4
4n-4
问题:此时我们能知道这个代数式的值是多少吗?
获取新知
(1)当n取4, 10, 13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值.
n=4时,4×4-4=12
n=10时,4×10-4=36
n=13时,4×13-4=48
n=25时,4×25-4=96
思考:
(2)对于n的同一个值,同学们得到的结果都相同吗?
相同
(3)总结:从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代数式相应的值.一个代数式,可以看做一个计算程序.
数值转换机
输入x
输入x
输出
输出
×6
-3
×6
-3
问题 观察下面的过程,完成表格.
数值转换机
输入x
输入x
输出
输出
×6
-3
×6
-3
输入x -2 -1/2 0 0.26 1/3 5/2 4.5
机器1的输出结果
机器2的输出结果
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
定 义:
像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值.这个过程叫做求代数式的值.
求代数式的值的概念
求下列代数式的值时,代入过程正确的是( )
1.当 时,
2.当 时,
3.当 时,
4.当 时,
4
活动二
(1)代入时,要“对号入座”,避免代错字母,其他符号不变;
(2)代数式中,代入数值以后原来省略的乘号一定要还原;
(3)若字母的值是负数或分数,将字母的值代入代数式时,应加上括号,原来的数字和运算符号都不能改变.
在代入数值时应注意
例1 根据下面a,b的值,求代数式 的值
(1)a=2,b=-6;
例题讲解
写出条件:当……时
抄写代数式
代入数值
计算
例1 根据下面a,b的值,求代数式 的值
(2)a=-10,b=4
例2 如图,已知长方体的高为h,底面是边长为a的正方形.当h=3,a=2时,分别求其体积V和表面积S.
解:因为V=a2h,S=2a2+4ah,
所以 当h=3,a=2时,
V=a2h=22×3=12,
S=2a2+4ah=2×22+4×2×3=32.
拓展 整体代入法求代数式的值
例3 已知x+y=5,xy=2,求代数式(x+y)2-5xy的值.
解:因为x+y=5,xy=2,
所以(x+y)2-5xy=52-5×2=25-10=15.
相同的代数式可以看作一个字母——整体代入
随堂演练
1. 下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.平行四边形具有的性质矩形都具有
B
1.当x=1时,代数式4-3x的值是( )
A.1 B.2 C.3 D.4
2.若 则x2-y3的值为( )
A.1 B.-1 C. D.2
3.如果2a+3b=5,那么4a+6b-7= .
已知a+b=5,ab=6 ,则ab-(a+b)=___.
A
C
3
1
4.根据下面a,b的值,求代数式a2-2ab-b2 和(a-b)2 的值:
(1)a= ,b=3; (2)a=5,b=3.
(2)当a=5,b=3时,a2-2ab-b2=52-2×5×3+32=25-30+9=4.
(a-b)2 =(5-3)2 =4.
(1)当a= ,b=3时,
解:
通过计算结果你发现了什么?
5.某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
(2)把x=37,y=15代入代数式,得
10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
(1)该旅游团应付的门票费是(10x+5y)元.
解:
6.某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 优惠办法
少于200元 不予优惠
低于500元但 不低于200元 九折优惠
500元或超过500元 其中500元部分给予九折优惠,
超过500元部分给予八折优惠
(1)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他应付款________元,当x大于或等于500元时,他应付款____________元(用含x的代数式表示);
(2)王老师一次性购物600元,他实际付款________元;
(3)王老师第一次购物用了170元,第二次购物用了387元,如果王老师将这两次的购物换作一次购买可以节省________元.
解: (1)0.9x;500×0.9+(x-500)×0.8;
(2) 500×0.9+(600-500)×0.8=530;
(3)200×0.9=180,500×0.9=450,
所以设第二次购物原价为x,则0.9x=387,x=430,两次购物的原价是170+430=600(元),所以如果一次购买只需530元,节省27元.
代数式的值
代数式的值
利用代数式的值解决实际问题
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
