6.5垂直关系 复习课 课件(共45张PPT)
文档属性
| 名称 | 6.5垂直关系 复习课 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 08:07:39 | ||
图片预览









文档简介
(共45张PPT)
§ 6.5 垂直关系
(复习课)
北师大(2019)必修2
环节一
课前自测
1.下列命题中不正确的是
A.如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面β
B.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
C.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
D.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ
1.根据面面垂直的性质,知A不正确,直线l可能平行平面β,也可能在平面β内.
2.设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
若α⊥β,因为α∩β=m,b β,b⊥m,所以根据两个平面垂直的性质定理可得b⊥α,又a?α,所以a⊥b;反过来,当a∥m时,因为b⊥m,且a,m共面,一定有b⊥a,但不能保证b⊥α,所以不能推出α⊥β.
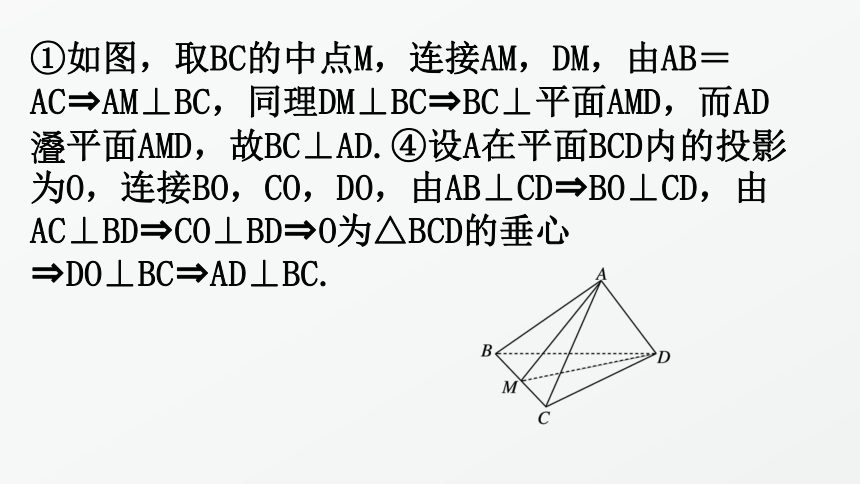
3.对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD;
②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;
④若AB⊥CD,AC⊥BD,则BC⊥AD.
其中为真命题的是
A.①② B.②③
C.②④ D.①④
①如图,取BC的中点M,连接AM,DM,由AB=AC AM⊥BC,同理DM⊥BC BC⊥平面AMD,而AD?平面AMD,故BC⊥AD.④设A在平面BCD内的投影为O,连接BO,CO,DO,由AB⊥CD BO⊥CD,由AC⊥BD CO⊥BD O为△BCD的垂心
DO⊥BC AD⊥BC.
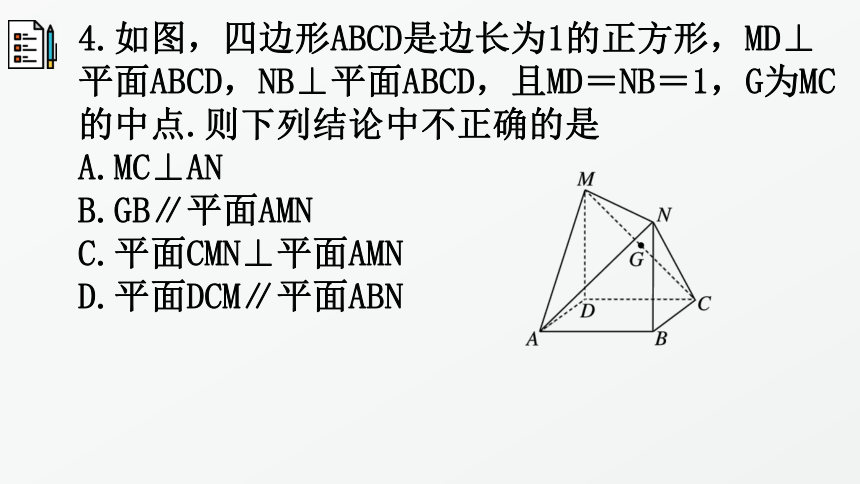
4.如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC的中点.则下列结论中不正确的是
A.MC⊥AN
B.GB∥平面AMN
C.平面CMN⊥平面AMN
D.平面DCM∥平面ABN
显然该几何图形为正方体截去两个三棱锥所剩的几何体,把该几何体放置到正方体中(如图),取AN的中点H,连接HB,MH,GB,则MC∥HB,又HB⊥AN,所以MC⊥AN,所以A正确;
由题意易得GB∥MH,又GB 平面AMN,MH?平面AMN,
所以GB∥平面AMN,所以B正确;
因为AB∥CD,DM∥BN,且AB∩BN=B,CD∩DM=D,所以平面DCM∥平面ABN,所以D正确.
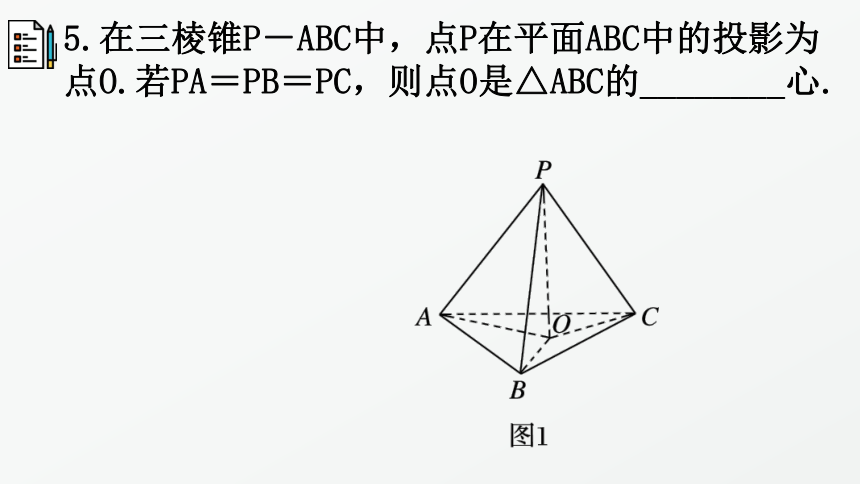
5.在三棱锥P-ABC中,点P在平面ABC中的投影为点O.若PA=PB=PC,则点O是△ABC的________心.
连接OA,OB,OC,OP,
在Rt△POA、Rt△POB和Rt△POC中,
PA=PC=PB,
所以OA=OB=OC,即O为△ABC的外心.
环节二
知识梳理
1.直线与平面垂直
图形 条件 结论
判 定 a⊥b,b α(b为α内的 一条直线) a⊥α
a⊥m,a⊥n,m、n α,________ a⊥α
任意
m∩n=O
判 定 a∥b,_______ b⊥α
性 质 a⊥α,______ a⊥b
a⊥α,b⊥α _____
a⊥α
b α
a∥b
2.平面与平面垂直
(1)平面与平面垂直的定义
两个平面相交,如果它们所成的二面角是 ,就说这两个平面互相垂直.
直二面角
2.平面与平面垂直
(2)判定定理与性质定理
文字语言 图形语言 符号语言
判 定 定理 如果一个平面经过另一个平面的一条 ,那么这两个平面互相垂直 α⊥β
垂线
性质定理 如果两个平面互相垂直,那么在一个平面内垂直于它们 的直线垂直于另一个平面 _____
交线
l⊥α
(1)若两平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(2)若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).
(3)垂直于同一条直线的两个平面平行.
(4)一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直.
锦囊妙计
体验1
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)直线l与平面α内的无数条直线都垂直,则l⊥α.( )
(2)垂直于同一个平面的两平面平行.( )
(3)直线a⊥α,b⊥α,则a∥b.( )
(4)若α⊥β,a⊥β a∥α.( )
(5)若直线a⊥平面α,直线b∥α,则直线a与b垂直.( )
×
×
√
×
√
环节三
合作探究
题型一 直线与平面垂直的判定与性质
例1如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF= ,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.OD′= .
证明:D′H⊥平面ABCD.
提炼
证明线面垂直的常用方法及关键
(1)证明直线和平面垂直的常用方法有:①判定定理;②垂直于平面的传递性(a∥b,a⊥α b⊥α);③面面平行的性质(a⊥α,α∥β a⊥β);④面面垂直的性质.
(2)证明线面垂直的关键是证线线垂直,而证明线线垂直则需借助线面垂直的性质.因此,判定定理与性质定理的合理转化是证明线面垂直的基本思想.
题型一 直线与平面垂直的判定与性质
体验2
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E.
求证: BC1⊥AB1.
因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC 平面ABC,
所以AC⊥CC1.
又因为AC⊥BC,CC1 平面BCC1B1,
BC 平面BCC1B1,BC∩CC1=C,
所以AC⊥平面BCC1B1.又因为BC1 平面BCC1B1,
所以BC1⊥AC.
因为BC=CC1,所以矩形BCC1B1是正方形,
因此BC1⊥B1C.
因为AC,B1C 平面B1AC,AC∩B1C=C,
所以BC1⊥平面B1AC.
又因为AB1 平面B1AC,
所以BC1⊥AB1.
题型二 平面与平面垂直的判定与性质
例2 如图,四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.
求证:平面EFG⊥平面EMN.
因为E、F分别为PB、AB的中点,所以EF∥PA.
又因为AB⊥PA,
所以EF⊥AB,同理可证AB⊥FG.
又因为EF∩FG=F,EF 平面EFG,FG 平面EFG.
所以AB⊥平面EFG.
又因为M,N分别为PD,PC的中点,
所以MN∥CD,又AB∥CD,所以MN∥AB,
所以MN⊥平面EFG.
又因为MN 平面EMN,所以平面EFG⊥平面EMN.
(1)判定面面垂直的方法
①面面垂直的定义;
②面面垂直的判定定理(a⊥β,a? α α⊥β).
(2)在已知平面垂直时,一般要用性质定理进行转化.
在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直.
提炼
题型二 平面与平面垂直的判定与性质
在本例条件下,证明:平面EMN⊥平面PAC.
体验3
因为AB⊥PA,AB⊥AC,
且PA∩AC=A,所以AB⊥平面PAC.
又MN∥CD,CD∥AB,所以MN∥AB,
所以MN⊥平面PAC.
又MN 平面EMN,
所以平面EMN⊥平面PAC.
题型三 垂直关系中的探索性问题
例3
如图,在三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在,请确定G点的位置;若不存在,请说明理由.
线段BE上存在点G,且BG= BE,使得平面DFG⊥平面CDE.
证明如下:
取CE的中点O,连接FO并延长交BE于点G,
连接GD,GF,∵CF=EF,∴GF⊥CE.
在三棱台ABC-DEF中,AB⊥BC DE⊥EF.
由CF⊥平面DEF CF⊥DE.
又CF∩EF=F,∴DE⊥平面CBEF,∴DE⊥GF.
题型三 垂直关系中的探索性问题
体验4
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC的中点.AB=BC,AC=2,AA1=,在棱BB1上是否存在点N,使得平面AC1N⊥平面AA1C1C?如果存在,求此时BNBB1的值;如果不存在,请说明理由. .
环节四
学以致用
1.若平面α⊥平面β,平面α∩平面β=直线l,则
A.垂直于平面β的平面一定平行于平面α
B.垂直于直线l的直线一定垂直于平面α
C.垂直于平面β的平面一定平行于直线l
D.垂直于直线l的平面一定与平面α,β都垂直
对于A,垂直于平面β的平面与平面α平行或相交,故A错误;
对于B,垂直于直线l的直线与平面α垂直、斜交、平行或在平面α内,故B错误;
对于C,垂直于平面β的平面与直线l平行或相交,故C错误;易知D正确.
2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
A中,m与n可垂直、可异面、可平行;
B中,m与n可平行、可异面;
C中,若α∥β,仍然满足m⊥n,m α,n β,故C错误;故选D.
如图,三棱柱ABC-A1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是
A.CC1与B1E是异面直线
B.AC⊥平面ABB1A1
C.AE与B1C1是异面直线,且AE⊥B1C1
D.A1C1∥平面AB1E
A不正确,因为CC1与B1E在同一个侧面中,故不是异面直线;
B不正确,由题意知,上底面ABC是一个正三角形,故不可能存在AC⊥平面ABB1A1;
C正确,因为AE,B1C1为在两个平行平面中且不平行的两条直线,故它们是异面直线;
D不正确,因为A1C1所在的平面与平面AB1E相交,且A1C1与交线有公共点,故A1C1∥平面AB1E不正确,故选C.
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC.
其中正确的是
A.①②④ B.①②③
C.②③④ D.①③④
由题意知,BD⊥平面ADC,故BD⊥AC,①正确;
AD为等腰直角三角形斜边BC上的高,平面ABD⊥平面ACD,所以AB=AC=BC,△BAC是等边三角形,②正确;
易知DA=DB=DC,又由②知③正确;
由①知④错.故选B.
§ 6.5 垂直关系
(复习课)
北师大(2019)必修2
环节一
课前自测
1.下列命题中不正确的是
A.如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面β
B.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
C.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
D.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ
1.根据面面垂直的性质,知A不正确,直线l可能平行平面β,也可能在平面β内.
2.设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
若α⊥β,因为α∩β=m,b β,b⊥m,所以根据两个平面垂直的性质定理可得b⊥α,又a?α,所以a⊥b;反过来,当a∥m时,因为b⊥m,且a,m共面,一定有b⊥a,但不能保证b⊥α,所以不能推出α⊥β.
3.对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD;
②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD;
④若AB⊥CD,AC⊥BD,则BC⊥AD.
其中为真命题的是
A.①② B.②③
C.②④ D.①④
①如图,取BC的中点M,连接AM,DM,由AB=AC AM⊥BC,同理DM⊥BC BC⊥平面AMD,而AD?平面AMD,故BC⊥AD.④设A在平面BCD内的投影为O,连接BO,CO,DO,由AB⊥CD BO⊥CD,由AC⊥BD CO⊥BD O为△BCD的垂心
DO⊥BC AD⊥BC.
4.如图,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,G为MC的中点.则下列结论中不正确的是
A.MC⊥AN
B.GB∥平面AMN
C.平面CMN⊥平面AMN
D.平面DCM∥平面ABN
显然该几何图形为正方体截去两个三棱锥所剩的几何体,把该几何体放置到正方体中(如图),取AN的中点H,连接HB,MH,GB,则MC∥HB,又HB⊥AN,所以MC⊥AN,所以A正确;
由题意易得GB∥MH,又GB 平面AMN,MH?平面AMN,
所以GB∥平面AMN,所以B正确;
因为AB∥CD,DM∥BN,且AB∩BN=B,CD∩DM=D,所以平面DCM∥平面ABN,所以D正确.
5.在三棱锥P-ABC中,点P在平面ABC中的投影为点O.若PA=PB=PC,则点O是△ABC的________心.
连接OA,OB,OC,OP,
在Rt△POA、Rt△POB和Rt△POC中,
PA=PC=PB,
所以OA=OB=OC,即O为△ABC的外心.
环节二
知识梳理
1.直线与平面垂直
图形 条件 结论
判 定 a⊥b,b α(b为α内的 一条直线) a⊥α
a⊥m,a⊥n,m、n α,________ a⊥α
任意
m∩n=O
判 定 a∥b,_______ b⊥α
性 质 a⊥α,______ a⊥b
a⊥α,b⊥α _____
a⊥α
b α
a∥b
2.平面与平面垂直
(1)平面与平面垂直的定义
两个平面相交,如果它们所成的二面角是 ,就说这两个平面互相垂直.
直二面角
2.平面与平面垂直
(2)判定定理与性质定理
文字语言 图形语言 符号语言
判 定 定理 如果一个平面经过另一个平面的一条 ,那么这两个平面互相垂直 α⊥β
垂线
性质定理 如果两个平面互相垂直,那么在一个平面内垂直于它们 的直线垂直于另一个平面 _____
交线
l⊥α
(1)若两平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(2)若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).
(3)垂直于同一条直线的两个平面平行.
(4)一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直.
锦囊妙计
体验1
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)直线l与平面α内的无数条直线都垂直,则l⊥α.( )
(2)垂直于同一个平面的两平面平行.( )
(3)直线a⊥α,b⊥α,则a∥b.( )
(4)若α⊥β,a⊥β a∥α.( )
(5)若直线a⊥平面α,直线b∥α,则直线a与b垂直.( )
×
×
√
×
√
环节三
合作探究
题型一 直线与平面垂直的判定与性质
例1如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF= ,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.OD′= .
证明:D′H⊥平面ABCD.
提炼
证明线面垂直的常用方法及关键
(1)证明直线和平面垂直的常用方法有:①判定定理;②垂直于平面的传递性(a∥b,a⊥α b⊥α);③面面平行的性质(a⊥α,α∥β a⊥β);④面面垂直的性质.
(2)证明线面垂直的关键是证线线垂直,而证明线线垂直则需借助线面垂直的性质.因此,判定定理与性质定理的合理转化是证明线面垂直的基本思想.
题型一 直线与平面垂直的判定与性质
体验2
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E.
求证: BC1⊥AB1.
因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC.
因为AC 平面ABC,
所以AC⊥CC1.
又因为AC⊥BC,CC1 平面BCC1B1,
BC 平面BCC1B1,BC∩CC1=C,
所以AC⊥平面BCC1B1.又因为BC1 平面BCC1B1,
所以BC1⊥AC.
因为BC=CC1,所以矩形BCC1B1是正方形,
因此BC1⊥B1C.
因为AC,B1C 平面B1AC,AC∩B1C=C,
所以BC1⊥平面B1AC.
又因为AB1 平面B1AC,
所以BC1⊥AB1.
题型二 平面与平面垂直的判定与性质
例2 如图,四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.
求证:平面EFG⊥平面EMN.
因为E、F分别为PB、AB的中点,所以EF∥PA.
又因为AB⊥PA,
所以EF⊥AB,同理可证AB⊥FG.
又因为EF∩FG=F,EF 平面EFG,FG 平面EFG.
所以AB⊥平面EFG.
又因为M,N分别为PD,PC的中点,
所以MN∥CD,又AB∥CD,所以MN∥AB,
所以MN⊥平面EFG.
又因为MN 平面EMN,所以平面EFG⊥平面EMN.
(1)判定面面垂直的方法
①面面垂直的定义;
②面面垂直的判定定理(a⊥β,a? α α⊥β).
(2)在已知平面垂直时,一般要用性质定理进行转化.
在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直.
提炼
题型二 平面与平面垂直的判定与性质
在本例条件下,证明:平面EMN⊥平面PAC.
体验3
因为AB⊥PA,AB⊥AC,
且PA∩AC=A,所以AB⊥平面PAC.
又MN∥CD,CD∥AB,所以MN∥AB,
所以MN⊥平面PAC.
又MN 平面EMN,
所以平面EMN⊥平面PAC.
题型三 垂直关系中的探索性问题
例3
如图,在三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在,请确定G点的位置;若不存在,请说明理由.
线段BE上存在点G,且BG= BE,使得平面DFG⊥平面CDE.
证明如下:
取CE的中点O,连接FO并延长交BE于点G,
连接GD,GF,∵CF=EF,∴GF⊥CE.
在三棱台ABC-DEF中,AB⊥BC DE⊥EF.
由CF⊥平面DEF CF⊥DE.
又CF∩EF=F,∴DE⊥平面CBEF,∴DE⊥GF.
题型三 垂直关系中的探索性问题
体验4
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC的中点.AB=BC,AC=2,AA1=,在棱BB1上是否存在点N,使得平面AC1N⊥平面AA1C1C?如果存在,求此时BNBB1的值;如果不存在,请说明理由. .
环节四
学以致用
1.若平面α⊥平面β,平面α∩平面β=直线l,则
A.垂直于平面β的平面一定平行于平面α
B.垂直于直线l的直线一定垂直于平面α
C.垂直于平面β的平面一定平行于直线l
D.垂直于直线l的平面一定与平面α,β都垂直
对于A,垂直于平面β的平面与平面α平行或相交,故A错误;
对于B,垂直于直线l的直线与平面α垂直、斜交、平行或在平面α内,故B错误;
对于C,垂直于平面β的平面与直线l平行或相交,故C错误;易知D正确.
2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
A中,m与n可垂直、可异面、可平行;
B中,m与n可平行、可异面;
C中,若α∥β,仍然满足m⊥n,m α,n β,故C错误;故选D.
如图,三棱柱ABC-A1B1C1中,侧棱AA1垂直底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是
A.CC1与B1E是异面直线
B.AC⊥平面ABB1A1
C.AE与B1C1是异面直线,且AE⊥B1C1
D.A1C1∥平面AB1E
A不正确,因为CC1与B1E在同一个侧面中,故不是异面直线;
B不正确,由题意知,上底面ABC是一个正三角形,故不可能存在AC⊥平面ABB1A1;
C正确,因为AE,B1C1为在两个平行平面中且不平行的两条直线,故它们是异面直线;
D不正确,因为A1C1所在的平面与平面AB1E相交,且A1C1与交线有公共点,故A1C1∥平面AB1E不正确,故选C.
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC.
其中正确的是
A.①②④ B.①②③
C.②③④ D.①③④
由题意知,BD⊥平面ADC,故BD⊥AC,①正确;
AD为等腰直角三角形斜边BC上的高,平面ABD⊥平面ACD,所以AB=AC=BC,△BAC是等边三角形,②正确;
易知DA=DB=DC,又由②知③正确;
由①知④错.故选B.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
