4.5.1函数的零点与方程的解 课件(共16张PPT)
文档属性
| 名称 | 4.5.1函数的零点与方程的解 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 08:10:31 | ||
图片预览






文档简介
(共16张PPT)
4.5.1函数的零点与方程的解
预习并回答下列问题:
(1)什么是函数零点?(函数零点的概念)
(2)求下列函数的零点?并画出相应函数的图像
f(x)=x2-2x-3 f(x)=x2-2x+1 f(x)=x2-2x+3
(3)怎么判断二次函数零点的个数?
(4)怎样求一个函数的零点?
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
(1)什么是函数零点?(函数零点的概念)
函数零点的概念:
零点是一个点吗
注意:
零点指的是一个实数。
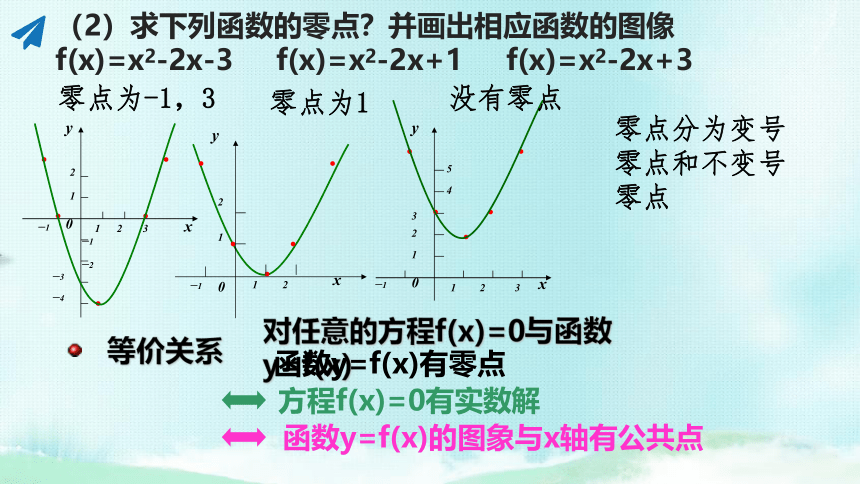
(2)求下列函数的零点?并画出相应函数的图像
f(x)=x2-2x-3 f(x)=x2-2x+1 f(x)=x2-2x+3
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
y
x
0
-1
2
1
1
2
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
零点分为变号零点和不变号零点
零点为-1,3
零点为1
没有零点
等价关系
对任意的方程f(x)=0与函数y=f(x)
函数y=f(x)有零点
函数y=f(x)的图象与x轴有公共点
方程f(x)=0有实数解
(3)怎么判断二次函数零点的个数?
对于二次函数 f(x)=ax2+bx+c(a≠0)
Δ > 0 ,
Δ =0 ,
Δ <0 ,
二次函数的零点有两个
二次函数的零点有一个
二次函数没有零点
例1:求下列函数零点
(1) (2)y=1-log2(x+3) (3)y=2x-1-3
解:(1)令y=0,则 =0,
解得x=-6
故该函数的零点为-6 .
(2)令y=0,则 1-log2(x+3) =0,
解得x=-1.
故该函数的零点为-1.
(3)令y=0,则2x-1 - 3=0,解得x=1+log23=log26.
故该函数零点为log26.
解:(1)令y=0,则lnx+2x-6=0
可变形为lnx= -2 x+6
即函数y=lnx与函数y= -2x+6图象交点的横坐标。
由图象可知:零点的大概区间为(2,3).
2
故n=2
解:(2)log2x+x=0
原方程的解可以转换为y=log2x与y= -x图象交点的横坐标。
x
y
0
-1
2
1
1
2
-1
-2
-3
-4
3
4
5
可变形为log2x= - x
由图知:方程的解所在的区间为(0,1).
1
故n=1
例3:若函数y=|x2-2x|-m,当m为何值时,该函数有两个零点?
解:令y=0,则|x2-2x|- m =0
可变形为|x2-2x|=m
原函数的零点可以转换为y=|x2-2x|与y=m图象交点的横坐标。
x
y
0
-1
2
1
1
2
-1
-2
3
4
由图象可知:m>1或m=0时,该函数有两个零点.
(4)怎样求一个函数的零点?
代数法:求方程的根,得出函数的零点.
图象法:
①作y=f(x)的函数图象,找出函数图象和 x 轴的交 点的横坐标.
②若F(x)=f(x)-g(x),则可以转换为y=f(x)与y=g(x)交点的横坐标
③若F(x)=f(x)-m,则可以转换为y=f(x)与y=m交点的横坐标
方法1
方法2
(可求出具体零点,零点个数及零点所在位置)
(可求出零点个数,零点大概区间)
练习:1.如图,该函数零点的个数有________个,零点为
_____________.
3
-4,-2,3
2
解:由题可知:ax2-x-1=0的解只有一个.
所以当a≠0时,
当a=0时,x=-1.符合题意。
故a=0或a= .
3.已知函数y=ax2-x-1只有一个零点,求a的值。
解得a=
Δ=1+4a=0.
x
y
0
-1
2
1
1
2
-1
-2
-3
-4
3
(0,1]
5.
解:当x>0时,由xln(x+1)=0,
得x=0
(舍)
当x≤0时,由2x2-3x-2=0,
(舍)
所以函数的零点为-
C
log3x=3 - x
y1=log3x与y2=3 - x交点的横坐标。
3
x
y
0
-1
2
1
1
2
-1
-2
-3
-4
3
4
5
B
谢谢!
4.5.1函数的零点与方程的解
预习并回答下列问题:
(1)什么是函数零点?(函数零点的概念)
(2)求下列函数的零点?并画出相应函数的图像
f(x)=x2-2x-3 f(x)=x2-2x+1 f(x)=x2-2x+3
(3)怎么判断二次函数零点的个数?
(4)怎样求一个函数的零点?
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
(1)什么是函数零点?(函数零点的概念)
函数零点的概念:
零点是一个点吗
注意:
零点指的是一个实数。
(2)求下列函数的零点?并画出相应函数的图像
f(x)=x2-2x-3 f(x)=x2-2x+1 f(x)=x2-2x+3
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
y
x
0
-1
2
1
1
2
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
零点分为变号零点和不变号零点
零点为-1,3
零点为1
没有零点
等价关系
对任意的方程f(x)=0与函数y=f(x)
函数y=f(x)有零点
函数y=f(x)的图象与x轴有公共点
方程f(x)=0有实数解
(3)怎么判断二次函数零点的个数?
对于二次函数 f(x)=ax2+bx+c(a≠0)
Δ > 0 ,
Δ =0 ,
Δ <0 ,
二次函数的零点有两个
二次函数的零点有一个
二次函数没有零点
例1:求下列函数零点
(1) (2)y=1-log2(x+3) (3)y=2x-1-3
解:(1)令y=0,则 =0,
解得x=-6
故该函数的零点为-6 .
(2)令y=0,则 1-log2(x+3) =0,
解得x=-1.
故该函数的零点为-1.
(3)令y=0,则2x-1 - 3=0,解得x=1+log23=log26.
故该函数零点为log26.
解:(1)令y=0,则lnx+2x-6=0
可变形为lnx= -2 x+6
即函数y=lnx与函数y= -2x+6图象交点的横坐标。
由图象可知:零点的大概区间为(2,3).
2
故n=2
解:(2)log2x+x=0
原方程的解可以转换为y=log2x与y= -x图象交点的横坐标。
x
y
0
-1
2
1
1
2
-1
-2
-3
-4
3
4
5
可变形为log2x= - x
由图知:方程的解所在的区间为(0,1).
1
故n=1
例3:若函数y=|x2-2x|-m,当m为何值时,该函数有两个零点?
解:令y=0,则|x2-2x|- m =0
可变形为|x2-2x|=m
原函数的零点可以转换为y=|x2-2x|与y=m图象交点的横坐标。
x
y
0
-1
2
1
1
2
-1
-2
3
4
由图象可知:m>1或m=0时,该函数有两个零点.
(4)怎样求一个函数的零点?
代数法:求方程的根,得出函数的零点.
图象法:
①作y=f(x)的函数图象,找出函数图象和 x 轴的交 点的横坐标.
②若F(x)=f(x)-g(x),则可以转换为y=f(x)与y=g(x)交点的横坐标
③若F(x)=f(x)-m,则可以转换为y=f(x)与y=m交点的横坐标
方法1
方法2
(可求出具体零点,零点个数及零点所在位置)
(可求出零点个数,零点大概区间)
练习:1.如图,该函数零点的个数有________个,零点为
_____________.
3
-4,-2,3
2
解:由题可知:ax2-x-1=0的解只有一个.
所以当a≠0时,
当a=0时,x=-1.符合题意。
故a=0或a= .
3.已知函数y=ax2-x-1只有一个零点,求a的值。
解得a=
Δ=1+4a=0.
x
y
0
-1
2
1
1
2
-1
-2
-3
-4
3
(0,1]
5.
解:当x>0时,由xln(x+1)=0,
得x=0
(舍)
当x≤0时,由2x2-3x-2=0,
(舍)
所以函数的零点为-
C
log3x=3 - x
y1=log3x与y2=3 - x交点的横坐标。
3
x
y
0
-1
2
1
1
2
-1
-2
-3
-4
3
4
5
B
谢谢!
同课章节目录
