重庆市五年(2017-2021)高考物理真题知识点分类汇编-计算题(20题,含答案)
文档属性
| 名称 | 重庆市五年(2017-2021)高考物理真题知识点分类汇编-计算题(20题,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-28 15:57:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
重庆市五年(2017-2021)高考物理真题知识点分类汇编-计算题(20题,含答案)
一.牛顿第二定律(共2小题)
1.(2020 新课标Ⅱ)如图,一竖直圆管质量为M,下端距水平地面的高度为H,顶端塞有一质量为m的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知M=4m,球和管之间的滑动摩擦力大小为4mg,g为重力加速度的大小,不计空气阻力。
(1)求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。
2.(2017 新课标Ⅱ)为提高冰球运动员的加速能力,教练员在冰面上与起跑线距离s0和s1(s1<s0)处分别设置一个挡板和一面小旗,如图所示。训练时,让运动员和冰球都位于起跑线上,教练员将冰球以速度v0击出,使冰球在冰面上沿垂直于起跑线的方向滑向挡板:冰球被击出的同时,运动员垂直于起跑线从静止出发滑向小旗。训练要求当冰球到达挡板时,运动员至少到达小旗处。假定运动员在滑行过程中做匀加速运动,冰球到达挡板时的速度为v1.重力加速度为g。求
(1)冰球与冰面之间的动摩擦因数;
(2)满足训练要求的运动员的最小加速度。
二.动量定理(共2小题)
3.(2021 重庆)我国规定摩托车、电动自行车骑乘人员必须依法配戴具有缓冲作用的安全头盔。小明对某轻质头盔的安全性能进行了模拟实验检测。某次,他在头盔中装入质量为5.0kg的物体(物体与头盔密切接触),使其从1.80m的高处自由落下(如图),并与水平地面发生碰撞,头盔厚度被挤压了0.03m时,物体的速度减小到零。挤压过程不计物体重力,且视为匀减速直线运动,不考虑物体和地面的形变,忽略空气阻力,重力加速度g取10m/s2。求:
(1)头盔接触地面前瞬间的速度大小;
(2)物体做匀减速直线运动的时间;
(3)物体在匀减速直线运动过程中所受平均作用力的大小。
4.(2019 新课标Ⅱ)一质量为m=2000kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中,司机突然发现前方100m处有一警示牌,立即刹车。刹车过程中,汽车所受阻力大小随时间的变化可简化为图(a)中的图线。图(a)中,0~t1时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略,汽车仍保持匀速行驶),t1=0.8s;t1~t2时间段为刹车系统的启动时间,t2=1.3s;从t2时刻开始汽车的刹车系统稳定工作,直至汽车停止。已知从t2时刻开始,汽车第1s内的位移为24m,第4s内的位移为1m。
(1)在图(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v﹣t图线;
(2)求t2时刻汽车的速度大小及此后的加速度大小;
(3)求刹车前汽车匀速行驶时的速度大小及t1~t2时间内汽车克服阻力做的功;从司机发现警示牌到汽车停止,汽车行驶的距离约为多少(以t1~t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度)?
三.动能定理(共1小题)
5.(2018 新课标Ⅱ)汽车A在水平冰雪路面上行驶,驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B,两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5m,A车向前滑动了2.0m,已知A和B的质量分别为2.0×103kg和1.5×103kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小g=10m/s2,求:
(1)碰撞后的瞬间B车速度的大小;
(2)碰撞前的瞬间A车速度的大小。
四.理想气体的状态方程(共5小题)
6.(2021 重庆)定高气球是种气象气球,充气完成后,其容积变化可以忽略。现有容积为V1的某气罐装有温度为T1、压强为p1的氦气,将该气罐与未充气的某定高气球连通充气。当充气完成后达到平衡状态后,气罐和球内的温度均为T1,压强均为kp1,k为常数。然后将气球密封并释放升空至某预定高度,气球内气体视为理想气体,假设全过程无漏气。
(1)求密封时定高气球内气体的体积;
(2)若在该预定高度球内气体重新达到平衡状态时的温度为T2,求此时气体的压强。
7.(2020 新课标Ⅱ)潜水钟是一种水下救生设备,它是一个底部开口、上部封闭的容器,外形与钟相似。潜水钟在水下时其内部上方空间里存有空气,以满足潜水员水下避险的需要。为计算方便,将潜水钟简化为截面积为S、高度为h、开口向下的圆筒;工作母船将潜水钟由水面上方开口向下吊放至深度为H的水下,如图所示。已知水的密度为ρ,重力加速度大小为g,大气压强为p0,H>>h,忽略温度的变化和水密度随深度的变化。
(i)求进入圆筒内水的高度l;
(ii)保持H不变,压入空气使筒内的水全部排出,求压入的空气在其压强为p0时的体积。
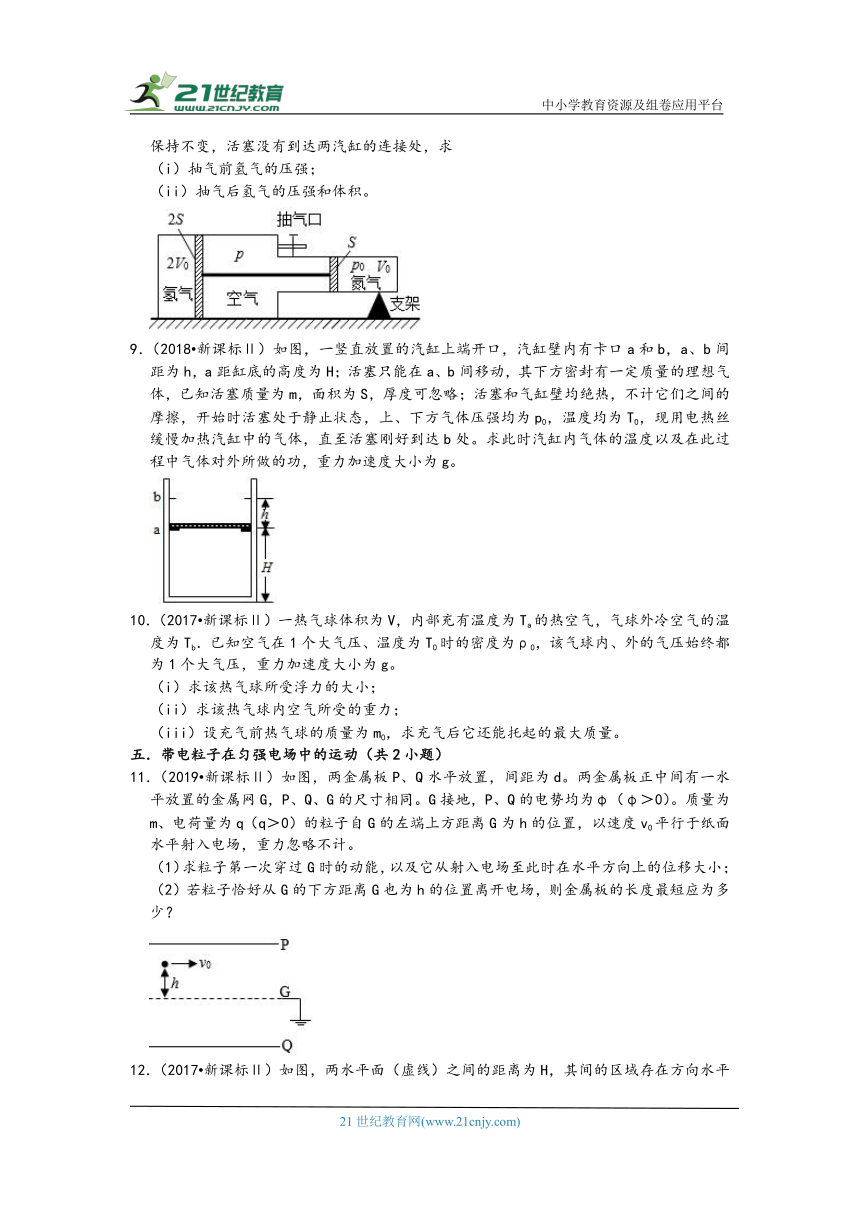
8.(2019 新课标Ⅱ)如图,一容器由横截面积分别为2S和S的两个汽缸连通而成,容器平放在水平地面上,汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p。现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两汽缸的连接处,求
(i)抽气前氢气的压强;
(ii)抽气后氢气的压强和体积。
9.(2018 新课标Ⅱ)如图,一竖直放置的汽缸上端开口,汽缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体,已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦,开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0,现用电热丝缓慢加热汽缸中的气体,直至活塞刚好到达b处。求此时汽缸内气体的温度以及在此过程中气体对外所做的功,重力加速度大小为g。
10.(2017 新课标Ⅱ)一热气球体积为V,内部充有温度为Ta的热空气,气球外冷空气的温度为Tb.已知空气在1个大气压、温度为T0时的密度为ρ0,该气球内、外的气压始终都为1个大气压,重力加速度大小为g。
(i)求该热气球所受浮力的大小;
(ii)求该热气球内空气所受的重力;
(iii)设充气前热气球的质量为m0,求充气后它还能托起的最大质量。
五.带电粒子在匀强电场中的运动(共2小题)
11.(2019 新课标Ⅱ)如图,两金属板P、Q水平放置,间距为d。两金属板正中间有一水平放置的金属网G,P、Q、G的尺寸相同。G接地,P、Q的电势均为φ(φ>0)。质量为m、电荷量为q(q>0)的粒子自G的左端上方距离G为h的位置,以速度v0平行于纸面水平射入电场,重力忽略不计。
(1)求粒子第一次穿过G时的动能,以及它从射入电场至此时在水平方向上的位移大小;
(2)若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为多少?
12.(2017 新课标Ⅱ)如图,两水平面(虚线)之间的距离为H,其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和﹣q(q>0)的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域,并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下;M在电场中做直线运动,刚离开电场时的动能为N刚离开电场时的动能的1.5倍。不计空气阻力,重力加速度大小为g。求
(1)M与N在电场中沿水平方向的位移之比;
(2)A点距电场上边界的高度;
(3)该电场的电场强度大小。
六.带电粒子在匀强磁场中的运动(共3小题)
13.(2021 重庆)如图1所示的Oxy竖直平面内,在原点O有一粒子源,可沿x轴正方向发射速度不同、比荷均为的带正电的粒子。在x≥L的区域仅有垂直于平面向内的匀强磁场;x<L的区域仅有如图2所示的电场,0~t0时间内和2t0时刻后的匀强电场大小相等,方向相反(0~t0时间内电场方向竖直向下),t0~2t0时间内电场强度为零。在磁场左边界x=L直线上的某点,固定一粒子收集器(图中未画出)。0时刻发射的A粒子在t0时刻经过左边界进入磁场,最终被收集器收集;B粒子在时刻以与A粒子相同的发射速度发射,第一次经过磁场左边界的位置坐标为;C粒子在t0时刻发射,其发射速度是A粒子发射速度的,不经过磁场能被收集器收集。忽略粒子间相互作用力和粒子重力,不考虑边界效应。
(1)求电场强度E的大小;
(2)求磁感应强度B的大小;
(3)设2t0时刻发射的粒子能被收集器收集,求其有可能的发射速度大小。
14.(2020 新课标Ⅱ)如图,在0≤x≤h,﹣∞<y<+∞区域中存在方向垂直于纸面的匀强磁场,磁感应强度B的大小可调,方向不变。一质量为m、电荷量为q(q>0)的粒子以速度v0从磁场区域左侧沿x轴进入磁场,不计重力。
(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值Bm;
(2)如果磁感应强度大小为,粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离。
15.(2018 新课标Ⅱ)一足够长的条状区域内存在匀强电场和匀强磁场,其在xOy平面内的截面如图所示;中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xOy平面;磁场的上、下两侧为电场区域,宽度均为l′,电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行。一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出。不计重力。
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点入射时速度的大小;
(3)若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为,求该粒子的比荷及其从M点运动到N点的时间。
七.光的折射定律(共4小题)
16.(2021 重庆)如图所示,一直角棱镜ABC,∠A=90°,AC=1。从AB边界面垂直入射的甲、乙两种不同频率的单色光,在棱镜中传播速度分别为k1c和k2c(0<k1<k2<1,c为真空中的光速),甲光第一次到达BC边恰好发生全反射。求:
(1)该棱镜分别对甲光和乙光的折射率;
(2)BC边的长度。
17.(2020 新课标Ⅱ)直角棱镜的折射率n=1.5,其横截面如图所示,图中∠C=90°,∠A=30°.截面内一细束与BC边平行的光线,从棱镜AB边上的D点射入,经折射后射到BC边上。
(i)光线在BC边上是否会发生全反射?说明理由;
(ii)不考虑多次反射,求从AC边射出的光线与最初的入射光线夹角的正弦值。
18.(2018 新课标Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°.一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出,EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
19.(2017 新课标Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
八.用双缝干涉测光的波长(共1小题)
20.(2019 新课标Ⅱ)某同学利用图示装置测量某种单色光的波长。实验时,接通电源使光源正常发光;调整光路,使得从目镜中可以观察到干涉条纹。回答下列问题:
(i)若想增加从目镜中观察到的条纹个数,该同学可 ;
A.将单缝向双缝靠近
B.将屏向靠近双缝的方向移动
C.将屏向远离双缝的方向移动
D.使用间距更小的双缝
(ii)若双缝的间距为d,屏与双缝间的距离为l,测得第1条暗条纹到第n条暗条纹之间的距离为△x,则单色光的波长λ= ;
(iii)某次测量时,选用的双缝的间距为0.300mm,测得屏与双缝间的距离为1.20m,第1条暗条纹到第4条暗条纹之间的距离为7.56mm。则所测单色光波长为 nm(结果保留3位有效数字)。
参考答案与试题解析
一.牛顿第二定律(共2小题)
1.(2020 新课标Ⅱ)如图,一竖直圆管质量为M,下端距水平地面的高度为H,顶端塞有一质量为m的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知M=4m,球和管之间的滑动摩擦力大小为4mg,g为重力加速度的大小,不计空气阻力。
(1)求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。
【解析】解:(1)管第一次落地弹起的瞬间,小球仍然向下运动,设此时管的加速度大小为a1,方向向下;球的加速度大小为a2,方向向上;球与管之间的摩擦力大小为f,由牛顿运动定律有:
Ma1=Mg+f
ma2=f﹣mg
联立并代入题给数据,得:
a1=2g
a2=3g;
(2)管第一次碰地前与球的速度大小相同,由运动学公式可得,碰地前瞬间它们的速度大小均为:
v0,方向均向下
管弹起的瞬间,管的速度反向,球的速度方向依然向下
设自弹起时经过时间t1,管与小球的速度刚好相同,取向上为正方向,由运动学公式可得:
v0﹣a1t1=﹣v0+a2t1
解得:t1
设此时管的下端离地高度为h1,速度为v,由运动学公式可得
h1=v0t1
v=v0﹣a1t1
由此可知此时v>0,此后,管与小球将以加速度g减速上升h2,到达最高点,由运动学公式有:h2
管第一次落地弹起后上升的最大高度H1=h1+h2;
(3)设第一次弹起过程中球相对管的位移为x1,在管开始下落到上升H1这一过程中,由动能定理有:
Mg(H﹣H1)+mg(H﹣H1+x1)﹣4mgx1=0
解得:x1
同理可推得,管与球从再次下落到第二次弹起至最高点的过程中,球与管的相对位移x2为:x2
设圆管长度为L.管第二次落地弹起后的上升过程中,球不会滑出管外的条件是x1+x2≤L
联立解得L应满足条件为:L。
【答案】(1)管第一次与地面碰撞后的瞬间,管和球各自的加速度大小分别为2g、3g;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,管上升的最大高度为;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,圆管长度应满足L。
2.(2017 新课标Ⅱ)为提高冰球运动员的加速能力,教练员在冰面上与起跑线距离s0和s1(s1<s0)处分别设置一个挡板和一面小旗,如图所示。训练时,让运动员和冰球都位于起跑线上,教练员将冰球以速度v0击出,使冰球在冰面上沿垂直于起跑线的方向滑向挡板:冰球被击出的同时,运动员垂直于起跑线从静止出发滑向小旗。训练要求当冰球到达挡板时,运动员至少到达小旗处。假定运动员在滑行过程中做匀加速运动,冰球到达挡板时的速度为v1.重力加速度为g。求
(1)冰球与冰面之间的动摩擦因数;
(2)满足训练要求的运动员的最小加速度。
【解析】解:(1)对冰球分析,根据速度位移公式得:,
加速度为:a,
根据牛顿第二定律得:a=μg,
解得冰球与冰面之间的动摩擦因数为:.
(2)设运动员的末速度为v2,根据两者运动时间相等,有:,
解得运动员到达小旗处的最小速度为:v2,
则最小加速度为:.
【答案】
(1)冰球与冰面之间的动摩擦因数为;
(2)满足训练要求的运动员的最小加速度为.
二.动量定理(共2小题)
3.(2021 重庆)我国规定摩托车、电动自行车骑乘人员必须依法配戴具有缓冲作用的安全头盔。小明对某轻质头盔的安全性能进行了模拟实验检测。某次,他在头盔中装入质量为5.0kg的物体(物体与头盔密切接触),使其从1.80m的高处自由落下(如图),并与水平地面发生碰撞,头盔厚度被挤压了0.03m时,物体的速度减小到零。挤压过程不计物体重力,且视为匀减速直线运动,不考虑物体和地面的形变,忽略空气阻力,重力加速度g取10m/s2。求:
(1)头盔接触地面前瞬间的速度大小;
(2)物体做匀减速直线运动的时间;
(3)物体在匀减速直线运动过程中所受平均作用力的大小。
【解析】解:(1)由自由落体运动规律可得:v2=2gh,其中:h=1.80m
代入数据解得:v=6m/s;
(2)由匀变速直线运动规律可得:,其中Δx=0.03m
代入数据解得:t=0.01s;
(3)取向下为正分向,由动量定理得:﹣Ft=0﹣mv
代入数据解得:F=3000N。
【答案】(1)头盔接触地面前瞬间的速度大小为6m/s;
(2)物体做匀减速直线运动的时间为0.01s;
(3)物体在匀减速直线运动过程中所受平均作用力的大小为3000N。
4.(2019 新课标Ⅱ)一质量为m=2000kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中,司机突然发现前方100m处有一警示牌,立即刹车。刹车过程中,汽车所受阻力大小随时间的变化可简化为图(a)中的图线。图(a)中,0~t1时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略,汽车仍保持匀速行驶),t1=0.8s;t1~t2时间段为刹车系统的启动时间,t2=1.3s;从t2时刻开始汽车的刹车系统稳定工作,直至汽车停止。已知从t2时刻开始,汽车第1s内的位移为24m,第4s内的位移为1m。
(1)在图(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v﹣t图线;
(2)求t2时刻汽车的速度大小及此后的加速度大小;
(3)求刹车前汽车匀速行驶时的速度大小及t1~t2时间内汽车克服阻力做的功;从司机发现警示牌到汽车停止,汽车行驶的距离约为多少(以t1~t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度)?
【解析】解:(1)v﹣t图象如图所示;
(2)设刹车前汽车匀速行驶的速度大小为v1,则t1时刻的速度也为v1,t2时刻的速度为v2,在t2时刻以后汽车做匀减速运动,设其加速度大小为a,取△t=1s,设汽车在t2+(n﹣1)△t~t2+n△t内的位移为sn,n=1、2、3…。
若汽车在t2+3△t~t2+4△t时间内未停止,设它在t2+3△t时刻的速度为v3,在t2+4△t时刻的速度为v4,根据运动学公式有:
s1﹣s4=3a(△t)2①
s1=v2△t②
v4=v2﹣4a△t ③
联立①②③式,代入数据解得:v4m/s ④
这说明在t2+4△t时刻前,汽车已经停止。因此,①式子不成立;
由于在t2+3△t~t2+4△t时间内汽车停止,根据运动学公式可得:
v3=v2﹣3a△t ⑤
2as4=v32⑥
联立②⑤⑥式,代入数据解得a=8m/s2,v2=28m/s ⑦
或者am/s2,v2=29.76m/s ⑧
但⑧式子情境下,v3<0,不合题意,舍去;
(3)设汽车的刹车系统稳定工作时,汽车所受阻力大小为f1,根据牛顿第二定律可得:
f1=ma ⑨
在t1~t2时间内,阻力对汽车冲量的大小为I⑩
根据动量定理可得:I=mv1﹣mv2,
根据动能定理,在t1~t2时间内,汽车克服阻力做的功为W
联立⑦⑨⑩ 式,代入数据可得:
v1=30m/s,
W=1.16×105J;
从司机发出警示牌到汽车停止,汽车行驶的距离s约为:
s=v1t1(v1+v2)(t2﹣t1)
联立⑦ ,代入数据解得s=87.5m。
【答案】(1)从司机发现警示牌到刹车系统稳定工作后汽车运动的v﹣t图线如图所示。
(2)t2时刻汽车的速度大小28m/s,此后的加速度大小为8m/s2;
(3)刹车前汽车匀速行驶时的速度大小为30m/s,t1~t2时间内汽车克服阻力做的功为1.16×105J;从司机发现警示牌到汽车停止,汽车行驶的距离约为87.5m。
三.动能定理(共1小题)
5.(2018 新课标Ⅱ)汽车A在水平冰雪路面上行驶,驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B,两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5m,A车向前滑动了2.0m,已知A和B的质量分别为2.0×103kg和1.5×103kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小g=10m/s2,求:
(1)碰撞后的瞬间B车速度的大小;
(2)碰撞前的瞬间A车速度的大小。
【解析】解:(1)以B车为研究对象,根据动能定理可得:
﹣μmBgxB=0
代入数据解得:vB=3m/s;
(2)设碰后A车速度大小为vA,碰前A车速度大小为v0,
碰后A车运动过程中,根据动能定理可得:
﹣μmAgxA=0,
代入数据解得:vA=2m/s;
两车碰撞过程中,取向右为正、根据动量守恒定律可得:
mAv0=mAvA+mBvB
代入数据解得:v0=4.25m/s。
【答案】(1)碰撞后的瞬间B车速度的大小为3m/s;
(2)碰撞前的瞬间A车速度的大小为4.25m/s。
四.理想气体的状态方程(共5小题)
6.(2021 重庆)定高气球是种气象气球,充气完成后,其容积变化可以忽略。现有容积为V1的某气罐装有温度为T1、压强为p1的氦气,将该气罐与未充气的某定高气球连通充气。当充气完成后达到平衡状态后,气罐和球内的温度均为T1,压强均为kp1,k为常数。然后将气球密封并释放升空至某预定高度,气球内气体视为理想气体,假设全过程无漏气。
(1)求密封时定高气球内气体的体积;
(2)若在该预定高度球内气体重新达到平衡状态时的温度为T2,求此时气体的压强。
【解析】解:(1)设密封时定高气球内气体体积为V,由玻意耳定律
p1V1=kp1(V1+V)
解得:
(2)由查理定律
解得
【答案】(1)密封时定高气球内气体的体积为;
(2)若在该预定高度球内气体重新达到平衡状态时的温度为T2,此时气体的压强为。
7.(2020 新课标Ⅱ)潜水钟是一种水下救生设备,它是一个底部开口、上部封闭的容器,外形与钟相似。潜水钟在水下时其内部上方空间里存有空气,以满足潜水员水下避险的需要。为计算方便,将潜水钟简化为截面积为S、高度为h、开口向下的圆筒;工作母船将潜水钟由水面上方开口向下吊放至深度为H的水下,如图所示。已知水的密度为ρ,重力加速度大小为g,大气压强为p0,H>>h,忽略温度的变化和水密度随深度的变化。
(i)求进入圆筒内水的高度l;
(ii)保持H不变,压入空气使筒内的水全部排出,求压入的空气在其压强为p0时的体积。
【解析】解:(i)设潜水钟在水面上方时和放入水下后筒内气体的体积分别为V0和V1,放入水下后筒内气体的压强为p1,由玻意耳定律和题给条件有:
p1V1=p0V0
V0=hS
V1=(h﹣l)S
p1=p0+ρg(H﹣l)
联立以上各式并考虑到H>>h>l,解得:l
(ⅱ)设水全部排出后筒内气体的压强为p2;此时筒内气体的体积为V0,这些气体在其压强为p0时的体积为V3,由玻意耳定律有:
p2V0=p0V3
其中p2=p0+ρgH
设需压入筒内的气体体积为V,依题意:
V=V3﹣V0
联立解得:V
【答案】(i)进入圆筒内水的高度l为;
(ii)保持H不变,压入空气使筒内的水全部排出,求压入的空气在其压强为p0时的体积为。
8.(2019 新课标Ⅱ)如图,一容器由横截面积分别为2S和S的两个汽缸连通而成,容器平放在水平地面上,汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p。现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两汽缸的连接处,求
(i)抽气前氢气的压强;
(ii)抽气后氢气的压强和体积。
【解析】解:(i)抽气前活塞静止处于平衡状态,
对活塞,由平衡条件得:(p氢﹣p) 2S=(p0﹣p)S,
解得,氢气的压强:p氢(p0+p);
(ii)设抽气后氢气的压强与体积分别为p1、V1,氮气的压强和体积分别为p2、V2,
对活塞,由平衡条件得:p2S=p1 2S,
气体发生等温变化,由玻意耳定律得:
p1V1=p氢 2V0
p2V2=p0V0,
由于两活塞用刚性杆连接,由几何关系得:
V1﹣2V0=2(V0﹣V2),
解得:p1p0p
V1;
【答案】(i)抽气前氢气的压强为(p0+p);
(ii)抽气后氢气的压强为p0p,体积为。
9.(2018 新课标Ⅱ)如图,一竖直放置的汽缸上端开口,汽缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体,已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦,开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0,现用电热丝缓慢加热汽缸中的气体,直至活塞刚好到达b处。求此时汽缸内气体的温度以及在此过程中气体对外所做的功,重力加速度大小为g。
【解析】解:设活塞刚要离开a处时汽缸内气体的温度为T1,活塞刚要离开a处时,设气体压强为p1;
在此段过程中,封闭气体作等容变化,根据查理定律得:
而p1
可得 T1
设活塞到达b处时汽缸内气体的温度为T′。
活塞上升过程,汽缸内气体作等压变化,则有
解得 T′
在此过程中气体对外所做的功 W=Fh=p1Sh=(p0S+mg)h
【答案】此时汽缸内气体的温度为,在此过程中气体对外所做的功为(p0S+mg)h。
10.(2017 新课标Ⅱ)一热气球体积为V,内部充有温度为Ta的热空气,气球外冷空气的温度为Tb.已知空气在1个大气压、温度为T0时的密度为ρ0,该气球内、外的气压始终都为1个大气压,重力加速度大小为g。
(i)求该热气球所受浮力的大小;
(ii)求该热气球内空气所受的重力;
(iii)设充气前热气球的质量为m0,求充气后它还能托起的最大质量。
【解析】解:(i)设1个大气压下质量为m的空气在温度为T0时的体积为V0,密度为
设温度为T的体积为VT,密度为
ρ(T)
由盖﹣吕萨克定律得
联立可得:ρ(T)
气球受到的浮力为f=ρ(Tb)gV
联立可得:f;
(ii)根据ρ(T)可得ρ(Ta),气球内空气的重力为G=ρ(Ta)gVgV;
(iii)气球要漂浮在空气中,则气球总重力等于冷空气的浮力,假如还能托起的最大质量为m则
F=m0g+G+mg
所以mm0
【答案】(i)气球受到的浮力为:gV;
(ii)气球内空气的重力为gV;
(iii)能托起的最大质量为m0。
五.带电粒子在匀强电场中的运动(共2小题)
11.(2019 新课标Ⅱ)如图,两金属板P、Q水平放置,间距为d。两金属板正中间有一水平放置的金属网G,P、Q、G的尺寸相同。G接地,P、Q的电势均为φ(φ>0)。质量为m、电荷量为q(q>0)的粒子自G的左端上方距离G为h的位置,以速度v0平行于纸面水平射入电场,重力忽略不计。
(1)求粒子第一次穿过G时的动能,以及它从射入电场至此时在水平方向上的位移大小;
(2)若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为多少?
【解析】解:(1)PG、QG间的电场强度大小相等、方向相反,设为E,则有:
E,
设粒子第一次到达G时动能为Ek,根据动能定理可得:
qEh=Ek
解得:Ek;
粒子在PG间运动的加速度为:a
此过程中粒子运动时间为t,则有:h
在水平方向上的位移大小为:x=v0t;
解得:x=v0
(2)若粒子穿过G一次就从电场的右侧飞出,则金属板的长度最短,根据对称性可知,此时金属板的长度为:
L=2x=2v0。
【答案】(1)粒子第一次穿过G时的动能;它从射入电场至此时在水平方向上的位移大小为v0;
(2)若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为2v0。
12.(2017 新课标Ⅱ)如图,两水平面(虚线)之间的距离为H,其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和﹣q(q>0)的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域,并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下;M在电场中做直线运动,刚离开电场时的动能为N刚离开电场时的动能的1.5倍。不计空气阻力,重力加速度大小为g。求
(1)M与N在电场中沿水平方向的位移之比;
(2)A点距电场上边界的高度;
(3)该电场的电场强度大小。
【解析】解:(1)两带电小球的电量相同,可知M球在电场中水平方向上做匀加速直线运动,N球在水平方向上做匀减速直线运动,水平方向上的加速度大小相等,
两球在竖直方向均受重力,竖直方向上做加速度为g的匀加速直线运动,由于竖直方向上的位移相等,则运动的时间相等,
设水平方向的加速度大小为a,
对M,有:,
对N:v0=at,,
可得,
解得xM:xN=3:1。
(2、3)设正电小球离开电场时的竖直分速度为vy,水平分速度为v1,两球离开电场时竖直分速度相等,
因为M在电场中做直线运动,刚离开电场时的动能为N刚离开电场时的动能的1.5倍,则有:,
解得,
因为v1=v0+at=2v0,则2v0,
因为M做直线运动,设小球进电场时在竖直方向上的分速度为vy1,则有:,解得vy1,
在竖直方向上有:,,
解得A点距电场上边界的高度h。
因为M做直线运动,合力方向与速度方向在同一条直线上,
有:,
则电场的电场强度E。
【答案】(1)M与N在电场中沿水平方向的位移之比为3:1
(2)A点距电场上边界的高度为;
(3)该电场的电场强度大小为。
六.带电粒子在匀强磁场中的运动(共3小题)
13.(2021 重庆)如图1所示的Oxy竖直平面内,在原点O有一粒子源,可沿x轴正方向发射速度不同、比荷均为的带正电的粒子。在x≥L的区域仅有垂直于平面向内的匀强磁场;x<L的区域仅有如图2所示的电场,0~t0时间内和2t0时刻后的匀强电场大小相等,方向相反(0~t0时间内电场方向竖直向下),t0~2t0时间内电场强度为零。在磁场左边界x=L直线上的某点,固定一粒子收集器(图中未画出)。0时刻发射的A粒子在t0时刻经过左边界进入磁场,最终被收集器收集;B粒子在时刻以与A粒子相同的发射速度发射,第一次经过磁场左边界的位置坐标为;C粒子在t0时刻发射,其发射速度是A粒子发射速度的,不经过磁场能被收集器收集。忽略粒子间相互作用力和粒子重力,不考虑边界效应。
(1)求电场强度E的大小;
(2)求磁感应强度B的大小;
(3)设2t0时刻发射的粒子能被收集器收集,求其有可能的发射速度大小。
【解析】解:(1)设A粒子发射速度为v,分别画出ABC粒子运动轨迹,如图1:
图1
根据题述可知
L=vt0
对B粒子沿y方向运动
qE=ma
联立解得:;
(2)设收集器的位置坐标为(L,y),
对C粒子:L=0.25v 4t0,
对A粒子:L=vt0,
A粒子进入磁场时沿x方向分速度为
沿y方向分速度
又
由几何关系得
解得:
A粒子进入磁场时的速度
由洛伦兹力提供向心力
解得:;
(3)设2t0时刻发射的粒子速度为v1,经电场偏转后直接被收集器收集,如图2,
图2
则有
解得:
设2t0时刻发射的粒子速度为v2,先经电场偏转,后进入磁场偏转后被收集器收集,如图2
L=v2t
y=y′+2r′cosα
由洛伦兹力提供向心力
v′cosα=v2
联立解得:,v'2,
所有可能的发射速度为:,,。
【答案】(1)电场强度E的大小为;
(2)磁感应强度B的大小为;
(3)设2t0时刻发射的粒子能被收集器收集,其有可能的发射速度大小为,,。
14.(2020 新课标Ⅱ)如图,在0≤x≤h,﹣∞<y<+∞区域中存在方向垂直于纸面的匀强磁场,磁感应强度B的大小可调,方向不变。一质量为m、电荷量为q(q>0)的粒子以速度v0从磁场区域左侧沿x轴进入磁场,不计重力。
(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值Bm;
(2)如果磁感应强度大小为,粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离。
【解析】解:(1)根据题意可知,粒子刚进入磁场时受到竖直向上的洛伦兹力,因此根据左手定则可知,磁场的方向垂直于纸面向里;
设粒子进入磁场中做圆周运动的半径为R,根据洛伦兹力公式和圆周运动的规律有:
由此可得:
粒子穿过y轴正半轴离开磁场,其在磁场中做圆周运动的圆心在y轴的正半轴上,半径应满足R≤h,由题意,当磁感应强度为Bm时,粒子的运动半径最大,由此可得:Bm;
(2)若磁感应强度大小为,粒子做圆周运动的圆心仍然在y轴的正半轴上,且此时的圆弧半径为:R′=2h,粒子会穿过图中P点离开磁场,运动轨迹如图所示:
,
设粒子在P点的运动方向与x轴的夹角为α,
根据几何知识有:
则有:30°
根据几何关系可得,P点与x轴的距离为:y=2h(1﹣cosα)=(2)h
【答案】(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,磁场的方向垂直于纸面向里,在这种情况下磁感应强度的最小值为;
(2)如果磁感应强度大小为,粒子将通过虚线所示边界上的一点离开磁场。粒子在该点的运动方向与x轴正方向的夹角为30°,该点到x轴的距离为(2)h。
15.(2018 新课标Ⅱ)一足够长的条状区域内存在匀强电场和匀强磁场,其在xOy平面内的截面如图所示;中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xOy平面;磁场的上、下两侧为电场区域,宽度均为l′,电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行。一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出。不计重力。
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点入射时速度的大小;
(3)若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为,求该粒子的比荷及其从M点运动到N点的时间。
【解析】解:(1)粒子在电场中的轨迹为抛物线,在磁场中的轨迹为圆弧,整个轨迹上下对称,故画出粒子运动的轨迹,如图所示,
(2)粒子从电场下边界入射后在电场中做类平抛运动,设粒子从M点射入时速度的大小为v0,在下侧电场中运动的时间为t,加速度大小为a,粒子的电荷量为q,质量为m,粒子进入磁场的速度大小为v,方向与电场方向的夹角为θ,运动轨迹对应的半径为R,如图所示,
根据牛顿第二定律可得:Eq=ma ①
速度沿电场方向的分量为:v1=at ②
垂直电场方向有:l′=v0t ③
根据几何关系可得:v1=vcosθ④
粒子在磁场中做匀速圆周运动,利用洛伦兹力提供向心力可得:qvB=m⑤
根据几何关系可得:l=2Rcosθ⑥
联立①②③④⑤⑥式可得粒子从M点入射时速度的大小:v0⑦
(3)根据几何关系可得速度沿电场方向的分量:v1⑧
联立①②③⑦⑧式可得该粒子的比荷:⑨
粒子在磁场中运动的周期:T⑩
粒子由M点到N点所用的时间:t′=2t T
联立③⑦⑨ 式可得:t′(1)
【答案】(1)定性画出该粒子在电磁场中运动的轨迹,如图所示;
(2)该粒子从M点入射时速度的大小为;
(3)该粒子的比荷为,其从M点运动到N点的时间(1)。
七.光的折射定律(共4小题)
16.(2021 重庆)如图所示,一直角棱镜ABC,∠A=90°,AC=1。从AB边界面垂直入射的甲、乙两种不同频率的单色光,在棱镜中传播速度分别为k1c和k2c(0<k1<k2<1,c为真空中的光速),甲光第一次到达BC边恰好发生全反射。求:
(1)该棱镜分别对甲光和乙光的折射率;
(2)BC边的长度。
【解析】解:(1)由光速与折射率的关系,可得该棱镜对甲光的折射率
该棱镜对乙光的折射率
(2)设BC边的长度为L,根据题述甲光第一次到达BC边恰好发生全反射,可画出光路图
根据全反射临界条件有:
根据几何关系有:cosC=sinθ
联立解得:
【答案】(1)该棱镜分别对甲光为,乙光的折射率为;
(2)BC边的长度为。
17.(2020 新课标Ⅱ)直角棱镜的折射率n=1.5,其横截面如图所示,图中∠C=90°,∠A=30°.截面内一细束与BC边平行的光线,从棱镜AB边上的D点射入,经折射后射到BC边上。
(i)光线在BC边上是否会发生全反射?说明理由;
(ii)不考虑多次反射,求从AC边射出的光线与最初的入射光线夹角的正弦值。
【解析】解:(i)光路图如图所示:
设光线在D点的入射角为i,折射角为r,折射光线射到BC边的E点,
设光线在E点的入射角为θ,根据几何关系有θ=90°﹣(30°﹣r)>60°…①
根据题中所给数据sin②
即θ大于全反射的临界角,因此光线在BC边上的E点会发生全反射;
(ii)设光线在AC边上的F点射出棱镜,光线的入射角为i′,折射角为r′,根据几何知识、反射定律以及折射定律有i=30°…③
i′=90°﹣θ…④
sini=nsinr…⑤
nsini′=sinr′…⑥
联立①③④⑤⑥解得:sinr′
根据几何知识可知,r′即AC边射出的光线与最初的入射光线的夹角。
【答案】(i)光线在BC边上会发生全反射;
(ii)不考虑多次反射,从AC边射出的光线与最初的入射光线夹角的正弦值为。
18.(2018 新课标Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°.一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出,EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
【解析】解:(i)由于D是CG的中点,GE⊥AC,根据几何关系可得:光束在D点发生折射时的折射角为γD=30°;
那么,根据几何关系可得:在E点的入射角、反射角均为γD+30°=60°;在F点的入射角为αF=30°;
那么,设入射角为αD,可得:折射角γF=αD,故出射光相对于D点的入射光的偏角为60°﹣αD+γF=60°;
(ii)由E点反射角为60°可得:EF∥BC;
故根据D点折射角为γD=30°,在F点的入射角为αF=30°可得:棱镜折射率;
根据光束在E点入射角为60°,发生全反射可得:,故棱镜折射率的取值范围为;
【答案】(i)出射光相对于D点的入射光的偏角为60°;
(ii)为实现上述光路,棱镜折射率的取值范围为。
19.(2017 新课标Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
【解析】解:设从光源发出的光直接射到D点的光线的入射角为i1,折射角为γ1,在剖面内做光源相对于镜面的对称点C,连接CD,交镜面与E点,由光源射向E点的光线反射后由ED射向D点,设入射角为i2,折射角为γ2,如图;
设液体的折射率为n,由折射定律:
nsini1=sinγ1
nsini2=sinγ2
由题意:γ1+γ2=90°
联立得:
由图中几何关系可得:;
联立得:n=1.55
【答案】该液体的折射率为1.55.
八.用双缝干涉测光的波长(共1小题)
20.(2019 新课标Ⅱ)某同学利用图示装置测量某种单色光的波长。实验时,接通电源使光源正常发光;调整光路,使得从目镜中可以观察到干涉条纹。回答下列问题:
(i)若想增加从目镜中观察到的条纹个数,该同学可 B ;
A.将单缝向双缝靠近
B.将屏向靠近双缝的方向移动
C.将屏向远离双缝的方向移动
D.使用间距更小的双缝
(ii)若双缝的间距为d,屏与双缝间的距离为l,测得第1条暗条纹到第n条暗条纹之间的距离为△x,则单色光的波长λ= ;
(iii)某次测量时,选用的双缝的间距为0.300mm,测得屏与双缝间的距离为1.20m,第1条暗条纹到第4条暗条纹之间的距离为7.56mm。则所测单色光波长为 630 nm(结果保留3位有效数字)。
【解析】解:(1)增加从目镜中观察到的条纹个数,则条纹的宽度减小,根据相邻亮条纹间的距离为△xλ,为减小相邻亮条纹(暗条纹)间的宽度,可增大双缝间距离或减小双缝到屏的距离;故B正确,ACD错误
故选:B;
(2)第1条暗条纹到第n条暗条纹之间的距离为△x,则两个相邻明纹(或暗纹)间的距离△x′
则单色光的波长λ
(3)将双缝的间距为0.300mm,测得屏与双缝间的距离为1.20m,以及n=4代入公式可得:λ=6.3×10﹣7m=630nm;
【答案】(1)B;
(2);
中小学教育资源及组卷应用平台
(3)63021世纪教育网(www.21cnjy.com)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
重庆市五年(2017-2021)高考物理真题知识点分类汇编-计算题(20题,含答案)
一.牛顿第二定律(共2小题)
1.(2020 新课标Ⅱ)如图,一竖直圆管质量为M,下端距水平地面的高度为H,顶端塞有一质量为m的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知M=4m,球和管之间的滑动摩擦力大小为4mg,g为重力加速度的大小,不计空气阻力。
(1)求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。
2.(2017 新课标Ⅱ)为提高冰球运动员的加速能力,教练员在冰面上与起跑线距离s0和s1(s1<s0)处分别设置一个挡板和一面小旗,如图所示。训练时,让运动员和冰球都位于起跑线上,教练员将冰球以速度v0击出,使冰球在冰面上沿垂直于起跑线的方向滑向挡板:冰球被击出的同时,运动员垂直于起跑线从静止出发滑向小旗。训练要求当冰球到达挡板时,运动员至少到达小旗处。假定运动员在滑行过程中做匀加速运动,冰球到达挡板时的速度为v1.重力加速度为g。求
(1)冰球与冰面之间的动摩擦因数;
(2)满足训练要求的运动员的最小加速度。
二.动量定理(共2小题)
3.(2021 重庆)我国规定摩托车、电动自行车骑乘人员必须依法配戴具有缓冲作用的安全头盔。小明对某轻质头盔的安全性能进行了模拟实验检测。某次,他在头盔中装入质量为5.0kg的物体(物体与头盔密切接触),使其从1.80m的高处自由落下(如图),并与水平地面发生碰撞,头盔厚度被挤压了0.03m时,物体的速度减小到零。挤压过程不计物体重力,且视为匀减速直线运动,不考虑物体和地面的形变,忽略空气阻力,重力加速度g取10m/s2。求:
(1)头盔接触地面前瞬间的速度大小;
(2)物体做匀减速直线运动的时间;
(3)物体在匀减速直线运动过程中所受平均作用力的大小。
4.(2019 新课标Ⅱ)一质量为m=2000kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中,司机突然发现前方100m处有一警示牌,立即刹车。刹车过程中,汽车所受阻力大小随时间的变化可简化为图(a)中的图线。图(a)中,0~t1时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略,汽车仍保持匀速行驶),t1=0.8s;t1~t2时间段为刹车系统的启动时间,t2=1.3s;从t2时刻开始汽车的刹车系统稳定工作,直至汽车停止。已知从t2时刻开始,汽车第1s内的位移为24m,第4s内的位移为1m。
(1)在图(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v﹣t图线;
(2)求t2时刻汽车的速度大小及此后的加速度大小;
(3)求刹车前汽车匀速行驶时的速度大小及t1~t2时间内汽车克服阻力做的功;从司机发现警示牌到汽车停止,汽车行驶的距离约为多少(以t1~t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度)?
三.动能定理(共1小题)
5.(2018 新课标Ⅱ)汽车A在水平冰雪路面上行驶,驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B,两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5m,A车向前滑动了2.0m,已知A和B的质量分别为2.0×103kg和1.5×103kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小g=10m/s2,求:
(1)碰撞后的瞬间B车速度的大小;
(2)碰撞前的瞬间A车速度的大小。
四.理想气体的状态方程(共5小题)
6.(2021 重庆)定高气球是种气象气球,充气完成后,其容积变化可以忽略。现有容积为V1的某气罐装有温度为T1、压强为p1的氦气,将该气罐与未充气的某定高气球连通充气。当充气完成后达到平衡状态后,气罐和球内的温度均为T1,压强均为kp1,k为常数。然后将气球密封并释放升空至某预定高度,气球内气体视为理想气体,假设全过程无漏气。
(1)求密封时定高气球内气体的体积;
(2)若在该预定高度球内气体重新达到平衡状态时的温度为T2,求此时气体的压强。
7.(2020 新课标Ⅱ)潜水钟是一种水下救生设备,它是一个底部开口、上部封闭的容器,外形与钟相似。潜水钟在水下时其内部上方空间里存有空气,以满足潜水员水下避险的需要。为计算方便,将潜水钟简化为截面积为S、高度为h、开口向下的圆筒;工作母船将潜水钟由水面上方开口向下吊放至深度为H的水下,如图所示。已知水的密度为ρ,重力加速度大小为g,大气压强为p0,H>>h,忽略温度的变化和水密度随深度的变化。
(i)求进入圆筒内水的高度l;
(ii)保持H不变,压入空气使筒内的水全部排出,求压入的空气在其压强为p0时的体积。
8.(2019 新课标Ⅱ)如图,一容器由横截面积分别为2S和S的两个汽缸连通而成,容器平放在水平地面上,汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p。现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两汽缸的连接处,求
(i)抽气前氢气的压强;
(ii)抽气后氢气的压强和体积。
9.(2018 新课标Ⅱ)如图,一竖直放置的汽缸上端开口,汽缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体,已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦,开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0,现用电热丝缓慢加热汽缸中的气体,直至活塞刚好到达b处。求此时汽缸内气体的温度以及在此过程中气体对外所做的功,重力加速度大小为g。
10.(2017 新课标Ⅱ)一热气球体积为V,内部充有温度为Ta的热空气,气球外冷空气的温度为Tb.已知空气在1个大气压、温度为T0时的密度为ρ0,该气球内、外的气压始终都为1个大气压,重力加速度大小为g。
(i)求该热气球所受浮力的大小;
(ii)求该热气球内空气所受的重力;
(iii)设充气前热气球的质量为m0,求充气后它还能托起的最大质量。
五.带电粒子在匀强电场中的运动(共2小题)
11.(2019 新课标Ⅱ)如图,两金属板P、Q水平放置,间距为d。两金属板正中间有一水平放置的金属网G,P、Q、G的尺寸相同。G接地,P、Q的电势均为φ(φ>0)。质量为m、电荷量为q(q>0)的粒子自G的左端上方距离G为h的位置,以速度v0平行于纸面水平射入电场,重力忽略不计。
(1)求粒子第一次穿过G时的动能,以及它从射入电场至此时在水平方向上的位移大小;
(2)若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为多少?
12.(2017 新课标Ⅱ)如图,两水平面(虚线)之间的距离为H,其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和﹣q(q>0)的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域,并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下;M在电场中做直线运动,刚离开电场时的动能为N刚离开电场时的动能的1.5倍。不计空气阻力,重力加速度大小为g。求
(1)M与N在电场中沿水平方向的位移之比;
(2)A点距电场上边界的高度;
(3)该电场的电场强度大小。
六.带电粒子在匀强磁场中的运动(共3小题)
13.(2021 重庆)如图1所示的Oxy竖直平面内,在原点O有一粒子源,可沿x轴正方向发射速度不同、比荷均为的带正电的粒子。在x≥L的区域仅有垂直于平面向内的匀强磁场;x<L的区域仅有如图2所示的电场,0~t0时间内和2t0时刻后的匀强电场大小相等,方向相反(0~t0时间内电场方向竖直向下),t0~2t0时间内电场强度为零。在磁场左边界x=L直线上的某点,固定一粒子收集器(图中未画出)。0时刻发射的A粒子在t0时刻经过左边界进入磁场,最终被收集器收集;B粒子在时刻以与A粒子相同的发射速度发射,第一次经过磁场左边界的位置坐标为;C粒子在t0时刻发射,其发射速度是A粒子发射速度的,不经过磁场能被收集器收集。忽略粒子间相互作用力和粒子重力,不考虑边界效应。
(1)求电场强度E的大小;
(2)求磁感应强度B的大小;
(3)设2t0时刻发射的粒子能被收集器收集,求其有可能的发射速度大小。
14.(2020 新课标Ⅱ)如图,在0≤x≤h,﹣∞<y<+∞区域中存在方向垂直于纸面的匀强磁场,磁感应强度B的大小可调,方向不变。一质量为m、电荷量为q(q>0)的粒子以速度v0从磁场区域左侧沿x轴进入磁场,不计重力。
(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值Bm;
(2)如果磁感应强度大小为,粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离。
15.(2018 新课标Ⅱ)一足够长的条状区域内存在匀强电场和匀强磁场,其在xOy平面内的截面如图所示;中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xOy平面;磁场的上、下两侧为电场区域,宽度均为l′,电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行。一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出。不计重力。
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点入射时速度的大小;
(3)若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为,求该粒子的比荷及其从M点运动到N点的时间。
七.光的折射定律(共4小题)
16.(2021 重庆)如图所示,一直角棱镜ABC,∠A=90°,AC=1。从AB边界面垂直入射的甲、乙两种不同频率的单色光,在棱镜中传播速度分别为k1c和k2c(0<k1<k2<1,c为真空中的光速),甲光第一次到达BC边恰好发生全反射。求:
(1)该棱镜分别对甲光和乙光的折射率;
(2)BC边的长度。
17.(2020 新课标Ⅱ)直角棱镜的折射率n=1.5,其横截面如图所示,图中∠C=90°,∠A=30°.截面内一细束与BC边平行的光线,从棱镜AB边上的D点射入,经折射后射到BC边上。
(i)光线在BC边上是否会发生全反射?说明理由;
(ii)不考虑多次反射,求从AC边射出的光线与最初的入射光线夹角的正弦值。
18.(2018 新课标Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°.一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出,EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
19.(2017 新课标Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
八.用双缝干涉测光的波长(共1小题)
20.(2019 新课标Ⅱ)某同学利用图示装置测量某种单色光的波长。实验时,接通电源使光源正常发光;调整光路,使得从目镜中可以观察到干涉条纹。回答下列问题:
(i)若想增加从目镜中观察到的条纹个数,该同学可 ;
A.将单缝向双缝靠近
B.将屏向靠近双缝的方向移动
C.将屏向远离双缝的方向移动
D.使用间距更小的双缝
(ii)若双缝的间距为d,屏与双缝间的距离为l,测得第1条暗条纹到第n条暗条纹之间的距离为△x,则单色光的波长λ= ;
(iii)某次测量时,选用的双缝的间距为0.300mm,测得屏与双缝间的距离为1.20m,第1条暗条纹到第4条暗条纹之间的距离为7.56mm。则所测单色光波长为 nm(结果保留3位有效数字)。
参考答案与试题解析
一.牛顿第二定律(共2小题)
1.(2020 新课标Ⅱ)如图,一竖直圆管质量为M,下端距水平地面的高度为H,顶端塞有一质量为m的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知M=4m,球和管之间的滑动摩擦力大小为4mg,g为重力加速度的大小,不计空气阻力。
(1)求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。
【解析】解:(1)管第一次落地弹起的瞬间,小球仍然向下运动,设此时管的加速度大小为a1,方向向下;球的加速度大小为a2,方向向上;球与管之间的摩擦力大小为f,由牛顿运动定律有:
Ma1=Mg+f
ma2=f﹣mg
联立并代入题给数据,得:
a1=2g
a2=3g;
(2)管第一次碰地前与球的速度大小相同,由运动学公式可得,碰地前瞬间它们的速度大小均为:
v0,方向均向下
管弹起的瞬间,管的速度反向,球的速度方向依然向下
设自弹起时经过时间t1,管与小球的速度刚好相同,取向上为正方向,由运动学公式可得:
v0﹣a1t1=﹣v0+a2t1
解得:t1
设此时管的下端离地高度为h1,速度为v,由运动学公式可得
h1=v0t1
v=v0﹣a1t1
由此可知此时v>0,此后,管与小球将以加速度g减速上升h2,到达最高点,由运动学公式有:h2
管第一次落地弹起后上升的最大高度H1=h1+h2;
(3)设第一次弹起过程中球相对管的位移为x1,在管开始下落到上升H1这一过程中,由动能定理有:
Mg(H﹣H1)+mg(H﹣H1+x1)﹣4mgx1=0
解得:x1
同理可推得,管与球从再次下落到第二次弹起至最高点的过程中,球与管的相对位移x2为:x2
设圆管长度为L.管第二次落地弹起后的上升过程中,球不会滑出管外的条件是x1+x2≤L
联立解得L应满足条件为:L。
【答案】(1)管第一次与地面碰撞后的瞬间,管和球各自的加速度大小分别为2g、3g;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,管上升的最大高度为;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,圆管长度应满足L。
2.(2017 新课标Ⅱ)为提高冰球运动员的加速能力,教练员在冰面上与起跑线距离s0和s1(s1<s0)处分别设置一个挡板和一面小旗,如图所示。训练时,让运动员和冰球都位于起跑线上,教练员将冰球以速度v0击出,使冰球在冰面上沿垂直于起跑线的方向滑向挡板:冰球被击出的同时,运动员垂直于起跑线从静止出发滑向小旗。训练要求当冰球到达挡板时,运动员至少到达小旗处。假定运动员在滑行过程中做匀加速运动,冰球到达挡板时的速度为v1.重力加速度为g。求
(1)冰球与冰面之间的动摩擦因数;
(2)满足训练要求的运动员的最小加速度。
【解析】解:(1)对冰球分析,根据速度位移公式得:,
加速度为:a,
根据牛顿第二定律得:a=μg,
解得冰球与冰面之间的动摩擦因数为:.
(2)设运动员的末速度为v2,根据两者运动时间相等,有:,
解得运动员到达小旗处的最小速度为:v2,
则最小加速度为:.
【答案】
(1)冰球与冰面之间的动摩擦因数为;
(2)满足训练要求的运动员的最小加速度为.
二.动量定理(共2小题)
3.(2021 重庆)我国规定摩托车、电动自行车骑乘人员必须依法配戴具有缓冲作用的安全头盔。小明对某轻质头盔的安全性能进行了模拟实验检测。某次,他在头盔中装入质量为5.0kg的物体(物体与头盔密切接触),使其从1.80m的高处自由落下(如图),并与水平地面发生碰撞,头盔厚度被挤压了0.03m时,物体的速度减小到零。挤压过程不计物体重力,且视为匀减速直线运动,不考虑物体和地面的形变,忽略空气阻力,重力加速度g取10m/s2。求:
(1)头盔接触地面前瞬间的速度大小;
(2)物体做匀减速直线运动的时间;
(3)物体在匀减速直线运动过程中所受平均作用力的大小。
【解析】解:(1)由自由落体运动规律可得:v2=2gh,其中:h=1.80m
代入数据解得:v=6m/s;
(2)由匀变速直线运动规律可得:,其中Δx=0.03m
代入数据解得:t=0.01s;
(3)取向下为正分向,由动量定理得:﹣Ft=0﹣mv
代入数据解得:F=3000N。
【答案】(1)头盔接触地面前瞬间的速度大小为6m/s;
(2)物体做匀减速直线运动的时间为0.01s;
(3)物体在匀减速直线运动过程中所受平均作用力的大小为3000N。
4.(2019 新课标Ⅱ)一质量为m=2000kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中,司机突然发现前方100m处有一警示牌,立即刹车。刹车过程中,汽车所受阻力大小随时间的变化可简化为图(a)中的图线。图(a)中,0~t1时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略,汽车仍保持匀速行驶),t1=0.8s;t1~t2时间段为刹车系统的启动时间,t2=1.3s;从t2时刻开始汽车的刹车系统稳定工作,直至汽车停止。已知从t2时刻开始,汽车第1s内的位移为24m,第4s内的位移为1m。
(1)在图(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v﹣t图线;
(2)求t2时刻汽车的速度大小及此后的加速度大小;
(3)求刹车前汽车匀速行驶时的速度大小及t1~t2时间内汽车克服阻力做的功;从司机发现警示牌到汽车停止,汽车行驶的距离约为多少(以t1~t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度)?
【解析】解:(1)v﹣t图象如图所示;
(2)设刹车前汽车匀速行驶的速度大小为v1,则t1时刻的速度也为v1,t2时刻的速度为v2,在t2时刻以后汽车做匀减速运动,设其加速度大小为a,取△t=1s,设汽车在t2+(n﹣1)△t~t2+n△t内的位移为sn,n=1、2、3…。
若汽车在t2+3△t~t2+4△t时间内未停止,设它在t2+3△t时刻的速度为v3,在t2+4△t时刻的速度为v4,根据运动学公式有:
s1﹣s4=3a(△t)2①
s1=v2△t②
v4=v2﹣4a△t ③
联立①②③式,代入数据解得:v4m/s ④
这说明在t2+4△t时刻前,汽车已经停止。因此,①式子不成立;
由于在t2+3△t~t2+4△t时间内汽车停止,根据运动学公式可得:
v3=v2﹣3a△t ⑤
2as4=v32⑥
联立②⑤⑥式,代入数据解得a=8m/s2,v2=28m/s ⑦
或者am/s2,v2=29.76m/s ⑧
但⑧式子情境下,v3<0,不合题意,舍去;
(3)设汽车的刹车系统稳定工作时,汽车所受阻力大小为f1,根据牛顿第二定律可得:
f1=ma ⑨
在t1~t2时间内,阻力对汽车冲量的大小为I⑩
根据动量定理可得:I=mv1﹣mv2,
根据动能定理,在t1~t2时间内,汽车克服阻力做的功为W
联立⑦⑨⑩ 式,代入数据可得:
v1=30m/s,
W=1.16×105J;
从司机发出警示牌到汽车停止,汽车行驶的距离s约为:
s=v1t1(v1+v2)(t2﹣t1)
联立⑦ ,代入数据解得s=87.5m。
【答案】(1)从司机发现警示牌到刹车系统稳定工作后汽车运动的v﹣t图线如图所示。
(2)t2时刻汽车的速度大小28m/s,此后的加速度大小为8m/s2;
(3)刹车前汽车匀速行驶时的速度大小为30m/s,t1~t2时间内汽车克服阻力做的功为1.16×105J;从司机发现警示牌到汽车停止,汽车行驶的距离约为87.5m。
三.动能定理(共1小题)
5.(2018 新课标Ⅱ)汽车A在水平冰雪路面上行驶,驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B,两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5m,A车向前滑动了2.0m,已知A和B的质量分别为2.0×103kg和1.5×103kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小g=10m/s2,求:
(1)碰撞后的瞬间B车速度的大小;
(2)碰撞前的瞬间A车速度的大小。
【解析】解:(1)以B车为研究对象,根据动能定理可得:
﹣μmBgxB=0
代入数据解得:vB=3m/s;
(2)设碰后A车速度大小为vA,碰前A车速度大小为v0,
碰后A车运动过程中,根据动能定理可得:
﹣μmAgxA=0,
代入数据解得:vA=2m/s;
两车碰撞过程中,取向右为正、根据动量守恒定律可得:
mAv0=mAvA+mBvB
代入数据解得:v0=4.25m/s。
【答案】(1)碰撞后的瞬间B车速度的大小为3m/s;
(2)碰撞前的瞬间A车速度的大小为4.25m/s。
四.理想气体的状态方程(共5小题)
6.(2021 重庆)定高气球是种气象气球,充气完成后,其容积变化可以忽略。现有容积为V1的某气罐装有温度为T1、压强为p1的氦气,将该气罐与未充气的某定高气球连通充气。当充气完成后达到平衡状态后,气罐和球内的温度均为T1,压强均为kp1,k为常数。然后将气球密封并释放升空至某预定高度,气球内气体视为理想气体,假设全过程无漏气。
(1)求密封时定高气球内气体的体积;
(2)若在该预定高度球内气体重新达到平衡状态时的温度为T2,求此时气体的压强。
【解析】解:(1)设密封时定高气球内气体体积为V,由玻意耳定律
p1V1=kp1(V1+V)
解得:
(2)由查理定律
解得
【答案】(1)密封时定高气球内气体的体积为;
(2)若在该预定高度球内气体重新达到平衡状态时的温度为T2,此时气体的压强为。
7.(2020 新课标Ⅱ)潜水钟是一种水下救生设备,它是一个底部开口、上部封闭的容器,外形与钟相似。潜水钟在水下时其内部上方空间里存有空气,以满足潜水员水下避险的需要。为计算方便,将潜水钟简化为截面积为S、高度为h、开口向下的圆筒;工作母船将潜水钟由水面上方开口向下吊放至深度为H的水下,如图所示。已知水的密度为ρ,重力加速度大小为g,大气压强为p0,H>>h,忽略温度的变化和水密度随深度的变化。
(i)求进入圆筒内水的高度l;
(ii)保持H不变,压入空气使筒内的水全部排出,求压入的空气在其压强为p0时的体积。
【解析】解:(i)设潜水钟在水面上方时和放入水下后筒内气体的体积分别为V0和V1,放入水下后筒内气体的压强为p1,由玻意耳定律和题给条件有:
p1V1=p0V0
V0=hS
V1=(h﹣l)S
p1=p0+ρg(H﹣l)
联立以上各式并考虑到H>>h>l,解得:l
(ⅱ)设水全部排出后筒内气体的压强为p2;此时筒内气体的体积为V0,这些气体在其压强为p0时的体积为V3,由玻意耳定律有:
p2V0=p0V3
其中p2=p0+ρgH
设需压入筒内的气体体积为V,依题意:
V=V3﹣V0
联立解得:V
【答案】(i)进入圆筒内水的高度l为;
(ii)保持H不变,压入空气使筒内的水全部排出,求压入的空气在其压强为p0时的体积为。
8.(2019 新课标Ⅱ)如图,一容器由横截面积分别为2S和S的两个汽缸连通而成,容器平放在水平地面上,汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p。现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两汽缸的连接处,求
(i)抽气前氢气的压强;
(ii)抽气后氢气的压强和体积。
【解析】解:(i)抽气前活塞静止处于平衡状态,
对活塞,由平衡条件得:(p氢﹣p) 2S=(p0﹣p)S,
解得,氢气的压强:p氢(p0+p);
(ii)设抽气后氢气的压强与体积分别为p1、V1,氮气的压强和体积分别为p2、V2,
对活塞,由平衡条件得:p2S=p1 2S,
气体发生等温变化,由玻意耳定律得:
p1V1=p氢 2V0
p2V2=p0V0,
由于两活塞用刚性杆连接,由几何关系得:
V1﹣2V0=2(V0﹣V2),
解得:p1p0p
V1;
【答案】(i)抽气前氢气的压强为(p0+p);
(ii)抽气后氢气的压强为p0p,体积为。
9.(2018 新课标Ⅱ)如图,一竖直放置的汽缸上端开口,汽缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体,已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦,开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0,现用电热丝缓慢加热汽缸中的气体,直至活塞刚好到达b处。求此时汽缸内气体的温度以及在此过程中气体对外所做的功,重力加速度大小为g。
【解析】解:设活塞刚要离开a处时汽缸内气体的温度为T1,活塞刚要离开a处时,设气体压强为p1;
在此段过程中,封闭气体作等容变化,根据查理定律得:
而p1
可得 T1
设活塞到达b处时汽缸内气体的温度为T′。
活塞上升过程,汽缸内气体作等压变化,则有
解得 T′
在此过程中气体对外所做的功 W=Fh=p1Sh=(p0S+mg)h
【答案】此时汽缸内气体的温度为,在此过程中气体对外所做的功为(p0S+mg)h。
10.(2017 新课标Ⅱ)一热气球体积为V,内部充有温度为Ta的热空气,气球外冷空气的温度为Tb.已知空气在1个大气压、温度为T0时的密度为ρ0,该气球内、外的气压始终都为1个大气压,重力加速度大小为g。
(i)求该热气球所受浮力的大小;
(ii)求该热气球内空气所受的重力;
(iii)设充气前热气球的质量为m0,求充气后它还能托起的最大质量。
【解析】解:(i)设1个大气压下质量为m的空气在温度为T0时的体积为V0,密度为
设温度为T的体积为VT,密度为
ρ(T)
由盖﹣吕萨克定律得
联立可得:ρ(T)
气球受到的浮力为f=ρ(Tb)gV
联立可得:f;
(ii)根据ρ(T)可得ρ(Ta),气球内空气的重力为G=ρ(Ta)gVgV;
(iii)气球要漂浮在空气中,则气球总重力等于冷空气的浮力,假如还能托起的最大质量为m则
F=m0g+G+mg
所以mm0
【答案】(i)气球受到的浮力为:gV;
(ii)气球内空气的重力为gV;
(iii)能托起的最大质量为m0。
五.带电粒子在匀强电场中的运动(共2小题)
11.(2019 新课标Ⅱ)如图,两金属板P、Q水平放置,间距为d。两金属板正中间有一水平放置的金属网G,P、Q、G的尺寸相同。G接地,P、Q的电势均为φ(φ>0)。质量为m、电荷量为q(q>0)的粒子自G的左端上方距离G为h的位置,以速度v0平行于纸面水平射入电场,重力忽略不计。
(1)求粒子第一次穿过G时的动能,以及它从射入电场至此时在水平方向上的位移大小;
(2)若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为多少?
【解析】解:(1)PG、QG间的电场强度大小相等、方向相反,设为E,则有:
E,
设粒子第一次到达G时动能为Ek,根据动能定理可得:
qEh=Ek
解得:Ek;
粒子在PG间运动的加速度为:a
此过程中粒子运动时间为t,则有:h
在水平方向上的位移大小为:x=v0t;
解得:x=v0
(2)若粒子穿过G一次就从电场的右侧飞出,则金属板的长度最短,根据对称性可知,此时金属板的长度为:
L=2x=2v0。
【答案】(1)粒子第一次穿过G时的动能;它从射入电场至此时在水平方向上的位移大小为v0;
(2)若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为2v0。
12.(2017 新课标Ⅱ)如图,两水平面(虚线)之间的距离为H,其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和﹣q(q>0)的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域,并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下;M在电场中做直线运动,刚离开电场时的动能为N刚离开电场时的动能的1.5倍。不计空气阻力,重力加速度大小为g。求
(1)M与N在电场中沿水平方向的位移之比;
(2)A点距电场上边界的高度;
(3)该电场的电场强度大小。
【解析】解:(1)两带电小球的电量相同,可知M球在电场中水平方向上做匀加速直线运动,N球在水平方向上做匀减速直线运动,水平方向上的加速度大小相等,
两球在竖直方向均受重力,竖直方向上做加速度为g的匀加速直线运动,由于竖直方向上的位移相等,则运动的时间相等,
设水平方向的加速度大小为a,
对M,有:,
对N:v0=at,,
可得,
解得xM:xN=3:1。
(2、3)设正电小球离开电场时的竖直分速度为vy,水平分速度为v1,两球离开电场时竖直分速度相等,
因为M在电场中做直线运动,刚离开电场时的动能为N刚离开电场时的动能的1.5倍,则有:,
解得,
因为v1=v0+at=2v0,则2v0,
因为M做直线运动,设小球进电场时在竖直方向上的分速度为vy1,则有:,解得vy1,
在竖直方向上有:,,
解得A点距电场上边界的高度h。
因为M做直线运动,合力方向与速度方向在同一条直线上,
有:,
则电场的电场强度E。
【答案】(1)M与N在电场中沿水平方向的位移之比为3:1
(2)A点距电场上边界的高度为;
(3)该电场的电场强度大小为。
六.带电粒子在匀强磁场中的运动(共3小题)
13.(2021 重庆)如图1所示的Oxy竖直平面内,在原点O有一粒子源,可沿x轴正方向发射速度不同、比荷均为的带正电的粒子。在x≥L的区域仅有垂直于平面向内的匀强磁场;x<L的区域仅有如图2所示的电场,0~t0时间内和2t0时刻后的匀强电场大小相等,方向相反(0~t0时间内电场方向竖直向下),t0~2t0时间内电场强度为零。在磁场左边界x=L直线上的某点,固定一粒子收集器(图中未画出)。0时刻发射的A粒子在t0时刻经过左边界进入磁场,最终被收集器收集;B粒子在时刻以与A粒子相同的发射速度发射,第一次经过磁场左边界的位置坐标为;C粒子在t0时刻发射,其发射速度是A粒子发射速度的,不经过磁场能被收集器收集。忽略粒子间相互作用力和粒子重力,不考虑边界效应。
(1)求电场强度E的大小;
(2)求磁感应强度B的大小;
(3)设2t0时刻发射的粒子能被收集器收集,求其有可能的发射速度大小。
【解析】解:(1)设A粒子发射速度为v,分别画出ABC粒子运动轨迹,如图1:
图1
根据题述可知
L=vt0
对B粒子沿y方向运动
qE=ma
联立解得:;
(2)设收集器的位置坐标为(L,y),
对C粒子:L=0.25v 4t0,
对A粒子:L=vt0,
A粒子进入磁场时沿x方向分速度为
沿y方向分速度
又
由几何关系得
解得:
A粒子进入磁场时的速度
由洛伦兹力提供向心力
解得:;
(3)设2t0时刻发射的粒子速度为v1,经电场偏转后直接被收集器收集,如图2,
图2
则有
解得:
设2t0时刻发射的粒子速度为v2,先经电场偏转,后进入磁场偏转后被收集器收集,如图2
L=v2t
y=y′+2r′cosα
由洛伦兹力提供向心力
v′cosα=v2
联立解得:,v'2,
所有可能的发射速度为:,,。
【答案】(1)电场强度E的大小为;
(2)磁感应强度B的大小为;
(3)设2t0时刻发射的粒子能被收集器收集,其有可能的发射速度大小为,,。
14.(2020 新课标Ⅱ)如图,在0≤x≤h,﹣∞<y<+∞区域中存在方向垂直于纸面的匀强磁场,磁感应强度B的大小可调,方向不变。一质量为m、电荷量为q(q>0)的粒子以速度v0从磁场区域左侧沿x轴进入磁场,不计重力。
(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值Bm;
(2)如果磁感应强度大小为,粒子将通过虚线所示边界上的一点离开磁场。求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离。
【解析】解:(1)根据题意可知,粒子刚进入磁场时受到竖直向上的洛伦兹力,因此根据左手定则可知,磁场的方向垂直于纸面向里;
设粒子进入磁场中做圆周运动的半径为R,根据洛伦兹力公式和圆周运动的规律有:
由此可得:
粒子穿过y轴正半轴离开磁场,其在磁场中做圆周运动的圆心在y轴的正半轴上,半径应满足R≤h,由题意,当磁感应强度为Bm时,粒子的运动半径最大,由此可得:Bm;
(2)若磁感应强度大小为,粒子做圆周运动的圆心仍然在y轴的正半轴上,且此时的圆弧半径为:R′=2h,粒子会穿过图中P点离开磁场,运动轨迹如图所示:
,
设粒子在P点的运动方向与x轴的夹角为α,
根据几何知识有:
则有:30°
根据几何关系可得,P点与x轴的距离为:y=2h(1﹣cosα)=(2)h
【答案】(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,磁场的方向垂直于纸面向里,在这种情况下磁感应强度的最小值为;
(2)如果磁感应强度大小为,粒子将通过虚线所示边界上的一点离开磁场。粒子在该点的运动方向与x轴正方向的夹角为30°,该点到x轴的距离为(2)h。
15.(2018 新课标Ⅱ)一足够长的条状区域内存在匀强电场和匀强磁场,其在xOy平面内的截面如图所示;中间是磁场区域,其边界与y轴垂直,宽度为l,磁感应强度的大小为B,方向垂直于xOy平面;磁场的上、下两侧为电场区域,宽度均为l′,电场强度的大小均为E,方向均沿x轴正方向;M、N为条状区域边界上的两点,它们的连线与y轴平行。一带正电的粒子以某一速度从M点沿y轴正方向射入电场,经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出。不计重力。
(1)定性画出该粒子在电磁场中运动的轨迹;
(2)求该粒子从M点入射时速度的大小;
(3)若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为,求该粒子的比荷及其从M点运动到N点的时间。
【解析】解:(1)粒子在电场中的轨迹为抛物线,在磁场中的轨迹为圆弧,整个轨迹上下对称,故画出粒子运动的轨迹,如图所示,
(2)粒子从电场下边界入射后在电场中做类平抛运动,设粒子从M点射入时速度的大小为v0,在下侧电场中运动的时间为t,加速度大小为a,粒子的电荷量为q,质量为m,粒子进入磁场的速度大小为v,方向与电场方向的夹角为θ,运动轨迹对应的半径为R,如图所示,
根据牛顿第二定律可得:Eq=ma ①
速度沿电场方向的分量为:v1=at ②
垂直电场方向有:l′=v0t ③
根据几何关系可得:v1=vcosθ④
粒子在磁场中做匀速圆周运动,利用洛伦兹力提供向心力可得:qvB=m⑤
根据几何关系可得:l=2Rcosθ⑥
联立①②③④⑤⑥式可得粒子从M点入射时速度的大小:v0⑦
(3)根据几何关系可得速度沿电场方向的分量:v1⑧
联立①②③⑦⑧式可得该粒子的比荷:⑨
粒子在磁场中运动的周期:T⑩
粒子由M点到N点所用的时间:t′=2t T
联立③⑦⑨ 式可得:t′(1)
【答案】(1)定性画出该粒子在电磁场中运动的轨迹,如图所示;
(2)该粒子从M点入射时速度的大小为;
(3)该粒子的比荷为,其从M点运动到N点的时间(1)。
七.光的折射定律(共4小题)
16.(2021 重庆)如图所示,一直角棱镜ABC,∠A=90°,AC=1。从AB边界面垂直入射的甲、乙两种不同频率的单色光,在棱镜中传播速度分别为k1c和k2c(0<k1<k2<1,c为真空中的光速),甲光第一次到达BC边恰好发生全反射。求:
(1)该棱镜分别对甲光和乙光的折射率;
(2)BC边的长度。
【解析】解:(1)由光速与折射率的关系,可得该棱镜对甲光的折射率
该棱镜对乙光的折射率
(2)设BC边的长度为L,根据题述甲光第一次到达BC边恰好发生全反射,可画出光路图
根据全反射临界条件有:
根据几何关系有:cosC=sinθ
联立解得:
【答案】(1)该棱镜分别对甲光为,乙光的折射率为;
(2)BC边的长度为。
17.(2020 新课标Ⅱ)直角棱镜的折射率n=1.5,其横截面如图所示,图中∠C=90°,∠A=30°.截面内一细束与BC边平行的光线,从棱镜AB边上的D点射入,经折射后射到BC边上。
(i)光线在BC边上是否会发生全反射?说明理由;
(ii)不考虑多次反射,求从AC边射出的光线与最初的入射光线夹角的正弦值。
【解析】解:(i)光路图如图所示:
设光线在D点的入射角为i,折射角为r,折射光线射到BC边的E点,
设光线在E点的入射角为θ,根据几何关系有θ=90°﹣(30°﹣r)>60°…①
根据题中所给数据sin②
即θ大于全反射的临界角,因此光线在BC边上的E点会发生全反射;
(ii)设光线在AC边上的F点射出棱镜,光线的入射角为i′,折射角为r′,根据几何知识、反射定律以及折射定律有i=30°…③
i′=90°﹣θ…④
sini=nsinr…⑤
nsini′=sinr′…⑥
联立①③④⑤⑥解得:sinr′
根据几何知识可知,r′即AC边射出的光线与最初的入射光线的夹角。
【答案】(i)光线在BC边上会发生全反射;
(ii)不考虑多次反射,从AC边射出的光线与最初的入射光线夹角的正弦值为。
18.(2018 新课标Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°.一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出,EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(i)求出射光相对于D点的入射光的偏角;
(ii)为实现上述光路,棱镜折射率的取值应在什么范围?
【解析】解:(i)由于D是CG的中点,GE⊥AC,根据几何关系可得:光束在D点发生折射时的折射角为γD=30°;
那么,根据几何关系可得:在E点的入射角、反射角均为γD+30°=60°;在F点的入射角为αF=30°;
那么,设入射角为αD,可得:折射角γF=αD,故出射光相对于D点的入射光的偏角为60°﹣αD+γF=60°;
(ii)由E点反射角为60°可得:EF∥BC;
故根据D点折射角为γD=30°,在F点的入射角为αF=30°可得:棱镜折射率;
根据光束在E点入射角为60°,发生全反射可得:,故棱镜折射率的取值范围为;
【答案】(i)出射光相对于D点的入射光的偏角为60°;
(ii)为实现上述光路,棱镜折射率的取值范围为。
19.(2017 新课标Ⅱ)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示.容器右侧内壁涂有反光材料,其他内壁涂有吸光材料.在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率.
【解析】解:设从光源发出的光直接射到D点的光线的入射角为i1,折射角为γ1,在剖面内做光源相对于镜面的对称点C,连接CD,交镜面与E点,由光源射向E点的光线反射后由ED射向D点,设入射角为i2,折射角为γ2,如图;
设液体的折射率为n,由折射定律:
nsini1=sinγ1
nsini2=sinγ2
由题意:γ1+γ2=90°
联立得:
由图中几何关系可得:;
联立得:n=1.55
【答案】该液体的折射率为1.55.
八.用双缝干涉测光的波长(共1小题)
20.(2019 新课标Ⅱ)某同学利用图示装置测量某种单色光的波长。实验时,接通电源使光源正常发光;调整光路,使得从目镜中可以观察到干涉条纹。回答下列问题:
(i)若想增加从目镜中观察到的条纹个数,该同学可 B ;
A.将单缝向双缝靠近
B.将屏向靠近双缝的方向移动
C.将屏向远离双缝的方向移动
D.使用间距更小的双缝
(ii)若双缝的间距为d,屏与双缝间的距离为l,测得第1条暗条纹到第n条暗条纹之间的距离为△x,则单色光的波长λ= ;
(iii)某次测量时,选用的双缝的间距为0.300mm,测得屏与双缝间的距离为1.20m,第1条暗条纹到第4条暗条纹之间的距离为7.56mm。则所测单色光波长为 630 nm(结果保留3位有效数字)。
【解析】解:(1)增加从目镜中观察到的条纹个数,则条纹的宽度减小,根据相邻亮条纹间的距离为△xλ,为减小相邻亮条纹(暗条纹)间的宽度,可增大双缝间距离或减小双缝到屏的距离;故B正确,ACD错误
故选:B;
(2)第1条暗条纹到第n条暗条纹之间的距离为△x,则两个相邻明纹(或暗纹)间的距离△x′
则单色光的波长λ
(3)将双缝的间距为0.300mm,测得屏与双缝间的距离为1.20m,以及n=4代入公式可得:λ=6.3×10﹣7m=630nm;
【答案】(1)B;
(2);
中小学教育资源及组卷应用平台
(3)63021世纪教育网(www.21cnjy.com)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
