沪科版数学八年级下册 18.1 勾股定理 课件(共25张)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理 课件(共25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 14:07:16 | ||
图片预览







文档简介
(共25张PPT)
18.1 勾股定理
除地球外,别的星球上有没有生命呢?
自古以来,人类就不断发出这样的疑问,特别是近年来不断出现的UFO事件,更让人们相信有外星人的说法,如果真的有,那我们怎么和他们交流呢?
我国著名数学家华罗庚在多年前曾提出这样的设想:向太空发射一种图形,因为这种图形在几千年前就已经被人类所认识,如果他们是“文明人”,也必定认识这种图形.
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。相传有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系.
A
B
C
我们也来观察右图的地面,你能发现A、B、C面积之间有什么数量关系吗?
SA+SB=SC
每块砖都是等腰直角三角形哦
A中含有____个小方格,
即A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
9
9
18
9
你能发现图1中正方形A、B、C的面积之间有什么数量关系吗? (图中每个小方格是1个单位面积)
细心观察
A
B
C
图1
结论:图1中三个正方形A,B,C的面积之间的数量关系是:
SA+SB=SC
SA+SB=SC在图2中还成立吗?
A
B
C
图2
结论:仍然成立。
A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
25
16
9
你是怎样得到正方形C的面积的?与同伴交流交流.
(图中每个小方格是1个单位面积)
在方格纸上,画
一个顶点都在格点
上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方
形,观察三个正方形面积之间的数量关系。
实验操作:
A
B
C
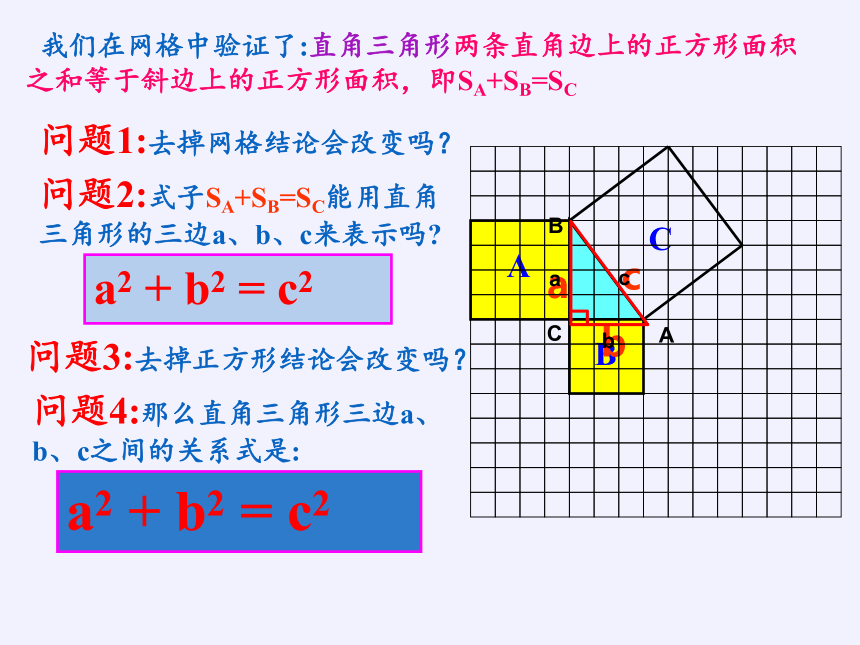
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗
问题4:那么直角三角形三边a、b、c之间的关系式是:
a
b
c
我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC
a2 + b2 = c2
a2 + b2 = c2
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
S1=a2
S2=b2
S3=c2
A
B
C
a
b
c
S1
S2
S3
S1+S2=S3
其中,
关系:
总结规律:
a2+b2=c2
故:
直角三角形两条直角边的平方和,等于斜边的平方。
文字表述:
探究验证:
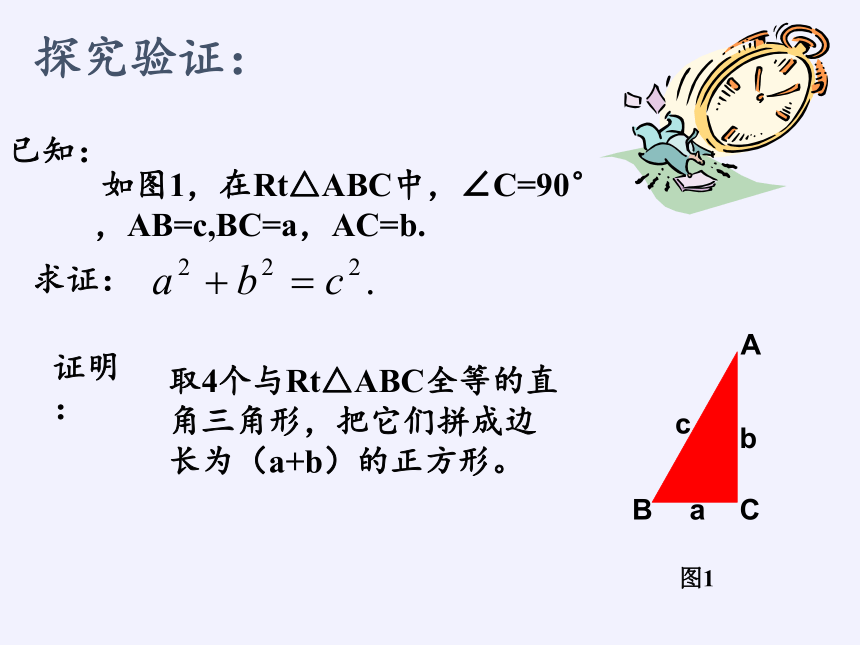
已知:
如图1,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
求证:
图1
a
A
B
C
c
b
证明:
取4个与Rt△ABC全等的直角三角形,把它们拼成边长为(a+b)的正方形。
证明a、b、c 之间的关系:
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用面积法证明
证明a、b、c 之间的关系:
a2 +b2 =c2
用面积法证明
证明a、b、c 之间的关系:
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
H
G
E
F
A1
B1
C1
D1
从图中可见,A1B1=B1C1=C1D1=A1D1=c.因为∠B1A1E+∠A1B1E=90°,而∠A1B1E=∠D1A1H,因此∠B1A1E+∠D1A1H=90°, ∠D1A1B1=90°.同理:∠A1B1C1=∠B1C1D1
=∠C1D1A1=90°,所以四边形A1B1C1D1是边长为c的正方形。
用面积法证明
∴a2+b2+2ab =c2+2ab
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
证明a、b、c 之间的关系:
a2 +b2 =c2
S正方形EFGH=4S直角三角形+ S正方形A1B1C1D1
∵S正方形EFGH=(a+b)2=a2+b2+2ab
a
a
a
a
b
b
b
b
c
c
c
c
H
G
E
F
A1
B1
C1
D1
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年第24届国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理
c
a
b
在西方又称毕达哥拉斯定理!
a2 + b2
c2 - b2
c2 - a2
=c2
=a2
=b2
为什么叫勾股定理这个名称呢?原来在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。于是我国古代学者就把直角三角形中较短直角边称为“勾”,较长直角边称为“股”,斜边称为“弦”.由于命题中反映的正好是直角三角形三边的关系,所以叫做勾股定理。
勾
股
勾 股 知 识
早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。
商高定理就是勾股定理哦!
百牛定理:
在国外,尤其在西方这个重要定理被称为“毕达哥拉斯定理”或“百牛定理”.相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现这个定理后异常高兴,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此又叫做“百牛定理”.
为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
求出下列直角三角形中未知边的长度.
y2+52=132
y2=132-52
y2=144
∴ y=12
在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
∵y>0
5
y
13
C
A
B
算一算
方法总结:利用勾股定理建立方程.
图中已知数据表示面积,求表示边的未知数x的值.
x
144
169
比一比:看谁算的快
在Rt△ABC中,∠C=90°.
已知: a:b=3:4, c=10,求a、b.
想一想
5 或
已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
1
1
美丽的勾股树
谈谈你的收获!
勇敢说一说!
1.这节课你的收获是什么?还有什么疑惑? 2.理解“勾股定理”应该注
意什么问题?
谢 谢
18.1 勾股定理
除地球外,别的星球上有没有生命呢?
自古以来,人类就不断发出这样的疑问,特别是近年来不断出现的UFO事件,更让人们相信有外星人的说法,如果真的有,那我们怎么和他们交流呢?
我国著名数学家华罗庚在多年前曾提出这样的设想:向太空发射一种图形,因为这种图形在几千年前就已经被人类所认识,如果他们是“文明人”,也必定认识这种图形.
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。相传有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系.
A
B
C
我们也来观察右图的地面,你能发现A、B、C面积之间有什么数量关系吗?
SA+SB=SC
每块砖都是等腰直角三角形哦
A中含有____个小方格,
即A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
9
9
18
9
你能发现图1中正方形A、B、C的面积之间有什么数量关系吗? (图中每个小方格是1个单位面积)
细心观察
A
B
C
图1
结论:图1中三个正方形A,B,C的面积之间的数量关系是:
SA+SB=SC
SA+SB=SC在图2中还成立吗?
A
B
C
图2
结论:仍然成立。
A的面积是 个单位面积.
B的面积是 个单位面积.
C的面积是 个单位面积.
25
16
9
你是怎样得到正方形C的面积的?与同伴交流交流.
(图中每个小方格是1个单位面积)
在方格纸上,画
一个顶点都在格点
上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方
形,观察三个正方形面积之间的数量关系。
实验操作:
A
B
C
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗
问题4:那么直角三角形三边a、b、c之间的关系式是:
a
b
c
我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC
a2 + b2 = c2
a2 + b2 = c2
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
S1=a2
S2=b2
S3=c2
A
B
C
a
b
c
S1
S2
S3
S1+S2=S3
其中,
关系:
总结规律:
a2+b2=c2
故:
直角三角形两条直角边的平方和,等于斜边的平方。
文字表述:
探究验证:
已知:
如图1,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
求证:
图1
a
A
B
C
c
b
证明:
取4个与Rt△ABC全等的直角三角形,把它们拼成边长为(a+b)的正方形。
证明a、b、c 之间的关系:
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用面积法证明
证明a、b、c 之间的关系:
a2 +b2 =c2
用面积法证明
证明a、b、c 之间的关系:
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
H
G
E
F
A1
B1
C1
D1
从图中可见,A1B1=B1C1=C1D1=A1D1=c.因为∠B1A1E+∠A1B1E=90°,而∠A1B1E=∠D1A1H,因此∠B1A1E+∠D1A1H=90°, ∠D1A1B1=90°.同理:∠A1B1C1=∠B1C1D1
=∠C1D1A1=90°,所以四边形A1B1C1D1是边长为c的正方形。
用面积法证明
∴a2+b2+2ab =c2+2ab
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
证明a、b、c 之间的关系:
a2 +b2 =c2
S正方形EFGH=4S直角三角形+ S正方形A1B1C1D1
∵S正方形EFGH=(a+b)2=a2+b2+2ab
a
a
a
a
b
b
b
b
c
c
c
c
H
G
E
F
A1
B1
C1
D1
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年第24届国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理
c
a
b
在西方又称毕达哥拉斯定理!
a2 + b2
c2 - b2
c2 - a2
=c2
=a2
=b2
为什么叫勾股定理这个名称呢?原来在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。于是我国古代学者就把直角三角形中较短直角边称为“勾”,较长直角边称为“股”,斜边称为“弦”.由于命题中反映的正好是直角三角形三边的关系,所以叫做勾股定理。
勾
股
勾 股 知 识
早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。
商高定理就是勾股定理哦!
百牛定理:
在国外,尤其在西方这个重要定理被称为“毕达哥拉斯定理”或“百牛定理”.相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现这个定理后异常高兴,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此又叫做“百牛定理”.
为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
求出下列直角三角形中未知边的长度.
y2+52=132
y2=132-52
y2=144
∴ y=12
在Rt△ABC中,由勾股定理得:AC2+BC2=AB2
∵y>0
5
y
13
C
A
B
算一算
方法总结:利用勾股定理建立方程.
图中已知数据表示面积,求表示边的未知数x的值.
x
144
169
比一比:看谁算的快
在Rt△ABC中,∠C=90°.
已知: a:b=3:4, c=10,求a、b.
想一想
5 或
已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .
试一试:
4
3
A
C
B
4
3
C
A
B
1
1
美丽的勾股树
谈谈你的收获!
勇敢说一说!
1.这节课你的收获是什么?还有什么疑惑? 2.理解“勾股定理”应该注
意什么问题?
谢 谢
