生活中的轴对称全章导学案
图片预览



文档简介
10.1 生活中的轴对称(1)
学习目标
1.通过折叠、剪出一个图形,使学生初步认识轴对称图形;
2.通过试验,观察、分析、归纳出轴对称图形概念,能用概念判断一个图形是否是轴对称图形;
3.培养学生的动手试验能力、归纳能力和语言表述能力。
学习重点、难点
轴对称图形的概念是学习重点,判断图形是否是轴对称图形既是学习重点又是学习难点。
学习过程
认真阅读课本80-81页,把你认为重点的部分作出适当的标注,并回答以下内容
一、 在实验操作中认识新知
1.请看以下图片,实际上它们都是轴对称图形。
自远古以来,对称形式被认为是和谐美丽、并且真实的,不论是在自然界中还是建筑里,甚至最普通的日常生活用品中,对称的形式随处可见,青山倒映在水中,这是令人难忘的对称景象。同学们可以想象,当你放学回家,落日、晚霞、还有远处的青山倒映在平静的水中,这样如诗如画的景致怎能不令人难忘,
2.试验
把一张半透明纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形
3.观察展示的图片和同学们剪出的图案,它们都什么共同点?
4、什么是轴对称图形?什么是对称轴
二、在练习中巩固新知
1请找出所剪的图案的对称轴,并且用直尺把它画出来。请回答你剪出的图形的对称轴是否只有一条?
2、请分别画出上一页中五个图形的对称轴来,请回答它们各有几条对称轴
3、完成课本82页的练习及习题1、2、
下列图形是轴对称图形吗?若是请画出它的对称轴来
三、在总结中升华新知
1、你认为什么样的图形是轴对称图形?什么样的图形是对称轴?
2、你还有什么收获?
3、你有什么困惑吗?
四、请收集一些落日、晚霞、还有青山、亭台、楼阁、鲜花等倒映在平静的水中的一些图片,体会轴对称给我们的生活带来的美的享受,感受生活中处处充满了数学
10.1 生活中的轴对称(2)
学习目的
通过回顾反思进一步认识轴对称图形。
通过动手实验,掌握关于某条直线成轴对称的两个图形的对应线段相等、对应角相等;理解轴对称图形和两个图形成轴对称这两个概念的区别与联系。
3、通过对比、分析认识两个图形成轴对称与轴对称图形两个概念的区别与联系
学习重点:轴对称图形的对应线段相等、对应角相等。
学习难点:两个图形成轴对称与轴对称图形两个概念的区别与联系。
学习过程:请仔细阅读课本82-83页,请把重点内容和你的困惑部分标出来
通过复习巩固知识
还记得轴对称及对称轴的概念吗?请写出来
2、请观察下列个三角形,它们都是轴对称图形吗?若是请画出对称轴来
等边三角形 等腰直角三角形 直角三角形
二、通过观察分析探索新知
1.试验:请分别剪掉右边的纸张,并把剪出的部分分别沿虚线部分对折,图形的左边部分和右边部分是否完全重合 满足这种特性的两个小蜜蜂图形和五边形就分别成轴对称。
2、什么样的图形成轴对称?什么是对称轴?什么是对称点?什么是对应线段?什么是对应角?
练习:在上图的(2)中,把A、B、C的对称点标出来。
4、 试验:在纸上滴上墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称 它的对称轴是哪一条 把它画出来。
5、如右图的两个三角形成轴对称,请量出三角形的边长和各内角的度数,比较一下这几个数据,有何结论?请思考该结论可以推广到一般情况吗?若可以请写出该结论来
6.轴对称图形与两个图形成轴对称的区别与联系.
如图(1),如果沿着虚线对折,直线两旁的部分会完全重合,那么这个图形就是轴对称图形;若把这个图形看成是左右两部分,则这两个图形就是关于虚线这条直线成轴对称。
如图(2),如果沿着虚线折叠,右边的图形会与左边的图形完全重合,那么就说这两个图形关于虚线这条直线成轴对称,若把(2)中的左右两个四边形看成是一个整体的图形,那么这个整体的图形是轴对称图形。
因此,轴对称图形和两个图形成轴对称的本质是相同的,只是怎么看图形的问题。
三、在练习中巩固新知
1.下面哪些选项的右边图形与左边图形成轴对称
2、完成课本82页3、4
3、如右图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等 哪些线段相等
4、如下图的特殊的四边形,请画出它们的对称轴来
并回答它们各有几条对称轴?
四、反思与收获
轴对称的认识
第1课时 简单的轴对称图形-------线段的垂直平分线
学习目的
1、通过动手试验,使学生知道线段是轴对称图形。
2、掌握线段的垂直子分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。
3、通过线段垂直平分线性质的概括提高分析概括能力
学习重点:线段垂直平分线上的点到线段两端的距离相等。
学习难点:运用线段垂直平分线性质解决问题。
学习过程
一、通过复习感知新知
1.轴对称图形的定义是什么
2.请猜想线段是轴对称图形吗
二、通过实验探索新知
1.认识线段是轴对称图形
试验1:按以下方法,看看线段是否是轴对称图形
在纸上画出线段AB和它的中点O,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合 线段是轴对称图形?
线段的对称轴是哪一条直线呢
2、线段垂直平分线的定义:垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线。如实验中的直线 CD就是线段AB的垂直平分线。
3、线段垂直平分线上性质
实验2:在以上试验的基础上,在直线CD上任意取一点M,连结 MA、MB,而后沿着直线CD折叠,观察MA和MB是否重合 再取一点试试,
实验三:有兴趣的同学请应用几何画板完成以上实验
通过以上实验,请分析概括出你的结论
4、请用几何语言表示出以上结论
三、提高练习巩固新知:
1、完成课本86页1
2、.如右图所示,△ABC中,AC=10,边BA的垂直平分线分别交AC、AB于点D、E,BC=6,求△BCD的周长。
3.如右图所示,DE和DF分别垂直平分线段 AB、BC,请猜想线段AD与线段CD有何关系 为什么
4、如图,AB垂直平分线段CD,垂足为点B,点E、F是AB上的点,CD=40,AB=35,则图中阴影部分的面积是
四、反思与收获.
10.2轴对称的认识(1)
学习目的
通过动手试验,知道角是轴对称图形,其对称轴是角平分线所在的直线,
通过类比设计出实验方法来验证角的对称性
通过类比实验总结出角平分线的性质,并能运用它解决相关问题。
学习重点:角平分线上的点到角两边的距离相等。
学习难点:运用角平分线性质解决问题。
学习过程
认真阅读课本86页并解决一下问题
一、通过复习引入新知
1、线段的对称轴是什么?它有什么样的性质?
2、线段垂直平分线的性质是如何得来的?
3、请猜想角的对称性?你能否类比线段对称性的实验方法设计一个实验角的对称性的实验?
二、通过实验探究新知新课
1、你的实验方法是:
2、你的实验结论是:
(1)
(2)
(3)你的结论用几何语言表示为
三、提高练习巩固新知:
1、完成课本86页练习2、3、4
2、如图,AD平分∠BAC,∠C=90°,DE⊥ AB,那么(1)DE和DC相等吗 为什么 (2)AE和AC相等吗 为什么
3、如图,在△ABC中,用直尺、量角器画∠A、∠B、∠C的平分线,看看三条角平分线有什么关系
4、如下图所示,在△ABC中,∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,DE=5, 求CD的长及∠A的度数
5、如上图(2),BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,求 P点到直线AB的距离。
四、反思与收获
10.2轴对称的认识(3)
学习目的
通过画图形的对称轴,发现用“连结对称点的线段被对称轴垂直平分”这一结论来验证一个图形是不是轴对称图形,
熟练画出轴对称图形的对称轴。
学习重点:画轴对称图形的对称轴。
学习难点:归纳总结画轴对称图形对称轴的方法。
学习过程
仔细阅读课本86-88页,并解决以下问题
一、通过复习感知新知
1.轴对称图形以及它的对称点是怎么定义的
2.看以下两个图形是否是轴对称图形 你能否画出它的对称轴
二、通过操作探究新知
1、试画出课本86页图10.2.5中两个图形的对称轴
2、试着画出下边两个图形的对称轴。
用折叠的方法检验所画的对称轴是否准确,如果准确的话,请你总结方法,并说出如何判断对称轴的位置。
3、对称轴的画法
首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
4、请写出轴对称图形的对称轴的结论
三、在应用中巩固新知
1、完成课本87页做一做
2、完成课本88页练习1、2、3
3、画出以下图形的对称轴
四、反思与收获
10.2轴对称的认识(4)
学习目的
1.通过在个点图中画轴对称图形体会画轴对称图形的方法
2、通过完成做一做中画最简单轴对称图形的方法进一步感知画轴对称图形的方法
3、通过阅读课本例题规范画轴对称图形的方法。体会画轴对称图形的关键实际上是画一些关键点的对称点,然后顺次连结就得到所要画的轴对称图形
4、通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。
学习重点、难点:能准确地画出轴对称图形。
学习过程
一、通过复习感知新知
1.什么是轴对称图形
2.请你标出图中,A、B、C三点的对称点。
A
B
C
二、在操作中探究新知
操作1.请尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
(1)你可以通过什么方法来验证你画的是否正确
(2)和其他同学比较一下,你的方法是最简单的吗
在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形吗
操作2.完成课本89页做一做
画好之后,你可以通过什么方法来验证一下A和 A′是否关于直线l对称
操作3、已知△ABC,直线l,画出△ABC关于直线l的对称图形。
(1)本题与上面的那些图比较有什么相同点和不同点
(2)你能否从上面的那些图的画法中得到启示,帮助你解决本题
A
B C
由以上操作可知:如果图形是由直线、线段或射线组成时,那么画出它关于某一条直线对称的图形时,只要画出图形中的特殊点(如线段的中点,角的顶点等)的对称点,然后连结对称点,就可以画出关于这条直线的对称图形。
三、在练习中巩固新知
1、 P90练习第1、2题。
2、P93习题1、2
3、如图画出一直三角形关于直线对称的图形来。观察你所画出的图形你能发现什么新的结论吗?
四、反思与收获
10.2轴对称的认识(5)
学习目的
1.学会设计简单的轴对称图案。
2.能够欣赏现实生活中的轴对称图形。
学习重点:利用对称轴进行图案设计。
学习难点;寻找对称轴以及如何利用对称轴作轴对称图形。
学习过程
一、通过复习引入
1.如图(1),请画出△ABC的关于直线l对称的图形。
2.如图(2),等边△ABC是轴对称图形吗 如果是,它有几条对称轴 画画试试看。
二、在操作中探究新知
在日常生活中,我们可以看到丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中往往有许多轴对称图形。请同学们欣赏P91四个装饰图案。
如图(3)是一个轴对称图形。
1.有多少条对称轴呢
2.可以利用轴对称性来画出它吗
请思考设计该图形的基本方案,对比以下步骤修改完善自己的方案
3、 请在下页正方形中,按以下5个步骤一起来画。
(1)在正方形纸片上画出四条对称轴。
(2)在其中一个三角形中,如图,画出图形形状的基本线条。(注意:不同的线条最终会得到不同的图案,你可以自己设计线条,而不必和书上一样。)
(3)按照其中一条斜的对称轴画出(2)中图形的对称图形。
(4)按照另一条斜的对称轴画出(3)中图形的对称图形。
(5)按照水平(或垂直)对称画出(4)中图形的对称图形,即得到图(3)中的图。
在图案上涂上你喜欢的颜色,擦掉其他的线条,轴对称的图案就完成了。
(6)思考:如何快速画出轴对称图案?
首先要画出对称轴,其次要画出图形形状的部分线条,然后根据对称性画出对称图形。
(7)你能否用几何画板快速地画出上述图案来?
4、如何用几何画板画出你设计的轴对称图形?请试一试。能否把你设计的图形展示给大家。请谈一下自己的收获
四、反思与收获
等腰三角形(1)
学习目的
1.通过学习了解等腰三角形的有关概念,掌握等腰三角形的性质。
2.通过探索等腰三角形的性质,进一步经历观察、实验、推理、交流等活动。
学习重点:等腰三角形等边对等角性质。
学习难点:通过操作,如何观察、分析、归纳得出等腰三角形性质。
学习过程
一、通过复习引入新课
1.在练习本上画一个等腰三角形,标出字母,回答什么样的三角形是等腰三角形 并指出等腰△ABC的腰、顶角、底角
2.日常生活中,哪些物体具有等腰三角形的形象
二、通过操作探究新知
1、实验。
请做一张等腰三角形的半透明纸片,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD,如图(2)所示,你能发现什么现象吗 请你尽可能多的写出结论。
2、请认真观察、思考、总结,可得到哪些结论?该结论如何表示成“如果……..那么……”的形式.
3、请用几何语言表示你的结论:
三、在练习中巩固新知
1、填空:在△ABC中,AB=AC,D在BC上,
如果AD⊥BC,那么∠BAD=∠______ ,BD=_______
如果∠BAD=∠CAD,那么AD⊥_____ ,BD=______
如果BD=CD,那么∠BAD=∠_______ ,AD⊥______
2、已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
3、已知:在△ABC中,AB=AC,∠A=80°,求∠B和∠C的度数。
4、练习1、2、3
5、如图,在△ABC中,AB=AC,AC⊥BD于点D,∠A=40°,求∠DBC的度数
6、如图,在△ABC中,AB=AC,DE是线段AB的垂直平分线。
(1)若∠A=40°,求∠C的度数
(2)若AB=12,BC=8,求△DBC的周长
四、反思与收获
等腰三角形(2)
学习目的
1.通过复习学会熟练运用等腰三角形的性质求等腰三角形内角的角度。
2.通过探究掌握等边三角形的性质。
学习重点,等腰三角形的性质及其应用。
学习难点:会简洁的逻辑推理。
学习过程
一、通过复习巩固等腰三角形的性质
1.叙述等腰三角形的性质,并回忆它是怎么得到的
等腰三角形的两个 相等,也可以简称“ ”。把等腰三角形对折,折叠两部分是互相重合的,即AB与AC重合,点B与点 C重合,线段BD与CD也重合,所以∠B=∠C。
等腰三角形的 互相重合,简称“三线合一”。由于AD为等腰三角形的对称轴,所以BD= CD,AD为底边上的中线;∠BAD=∠CAD,AD为顶角平分线,∠ADB=∠ADC=90°,AD又为底边上的高,因此“三线合一”。
2.若等腰三角形的两边长为3和4,则其周长为多少
二、通过实验探究新知
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。我们把三条边都相等的三角形叫做 三角形。等边三角形也称为正三角形。
等边三角形具有什么性质呢
请同学们画一个等边三角形,用量角器
量出各个内角的度数,并提出猜想。
你能否用已知的知识,通过推理得到你的猜想是正确的
3.上面的条件和结论如何叙述
等边三角形的 都相等,并且每一个角都等于 。
4、等边三角形是轴对称图形吗 如果是,有几条对称轴
三、在练习中巩固新知
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合( )
b.有一个角是60°的等腰三角形,其它两个内角也为60°( )
2.如图(2),在△ABC中,已知AB=AC,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。
3、如图,△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
4、已知AD是等腰△ABC的腰BC边上的高,∠DAB=60°,求这个三角形各内角的度数
四、反思与收获
等腰三角形(3)
学习目的
1.通过操作探索一个三角形是等腰三角形的条件。
2.能利用一个三角形是等腰三角形的条件,正确判断某个三角形是否为等腰三角形。
学习重点:让学生掌握一个三角形是等腰三角形的条件和正确应用。
学习难点:一个三角形是等腰三角形的条件的正确文字叙述。
一、通过复习引入新知
1、 等腰三角形具有哪些性质
2、等腰三角形的性质是怎么得到的
二、通过操作探究新知
1、对于一个三角形,怎样识别它是不是等腰三角形呢
2、等腰三角形的判定
请拿出一张半透明纸,做一个实验,按以下方法进行操作:
(1).在半透明纸上画一条线段BC。
(2).以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的角,两角终边的交点为A。
(3).用刻度尺找出BC的中点D,连接AD,然后沿AD对折。
问题1:AB与AC是否重合
问题2:本实验的条件与结论如何用文字语言加以叙述
问题3:本实验的条件与结论如何用几何语言加以叙述
问题4:三个角都是60°的三角形是等边三角形吗 你能说明理由吗
3.等腰直角三角形的有关概念:
你认为什么样的三角形为等腰直角三角形?
问题5:你能说出等腰直角三角形各角的大小吗
问题6:请你画一个等腰直角三角形,使∠C=90°,CD是底边上的高,数一数图中共有几个等腰直角三角形
三、在练习中巩固新知
1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
2.在△ABC中,已知AB=AC,BE、CF分别是∠ABC、
∠ACB的平分线,交于点O, 请猜想△OBC的形状,并说出理由
3、如图,△ABC是等边三角形,BD是△ABC的高,延长BC到点E,使CE=CD,试判断△BDE的形状,并说明理由
4、等腰三角形一腰上的高与另一腰的夹角为40°,求这个等腰三角形的底角的度数。
四、反思与收获
学习目标
1.通过折叠、剪出一个图形,使学生初步认识轴对称图形;
2.通过试验,观察、分析、归纳出轴对称图形概念,能用概念判断一个图形是否是轴对称图形;
3.培养学生的动手试验能力、归纳能力和语言表述能力。
学习重点、难点
轴对称图形的概念是学习重点,判断图形是否是轴对称图形既是学习重点又是学习难点。
学习过程
认真阅读课本80-81页,把你认为重点的部分作出适当的标注,并回答以下内容
一、 在实验操作中认识新知
1.请看以下图片,实际上它们都是轴对称图形。
自远古以来,对称形式被认为是和谐美丽、并且真实的,不论是在自然界中还是建筑里,甚至最普通的日常生活用品中,对称的形式随处可见,青山倒映在水中,这是令人难忘的对称景象。同学们可以想象,当你放学回家,落日、晚霞、还有远处的青山倒映在平静的水中,这样如诗如画的景致怎能不令人难忘,
2.试验
把一张半透明纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形
3.观察展示的图片和同学们剪出的图案,它们都什么共同点?
4、什么是轴对称图形?什么是对称轴
二、在练习中巩固新知
1请找出所剪的图案的对称轴,并且用直尺把它画出来。请回答你剪出的图形的对称轴是否只有一条?
2、请分别画出上一页中五个图形的对称轴来,请回答它们各有几条对称轴
3、完成课本82页的练习及习题1、2、
下列图形是轴对称图形吗?若是请画出它的对称轴来
三、在总结中升华新知
1、你认为什么样的图形是轴对称图形?什么样的图形是对称轴?
2、你还有什么收获?
3、你有什么困惑吗?
四、请收集一些落日、晚霞、还有青山、亭台、楼阁、鲜花等倒映在平静的水中的一些图片,体会轴对称给我们的生活带来的美的享受,感受生活中处处充满了数学
10.1 生活中的轴对称(2)
学习目的
通过回顾反思进一步认识轴对称图形。
通过动手实验,掌握关于某条直线成轴对称的两个图形的对应线段相等、对应角相等;理解轴对称图形和两个图形成轴对称这两个概念的区别与联系。
3、通过对比、分析认识两个图形成轴对称与轴对称图形两个概念的区别与联系
学习重点:轴对称图形的对应线段相等、对应角相等。
学习难点:两个图形成轴对称与轴对称图形两个概念的区别与联系。
学习过程:请仔细阅读课本82-83页,请把重点内容和你的困惑部分标出来
通过复习巩固知识
还记得轴对称及对称轴的概念吗?请写出来
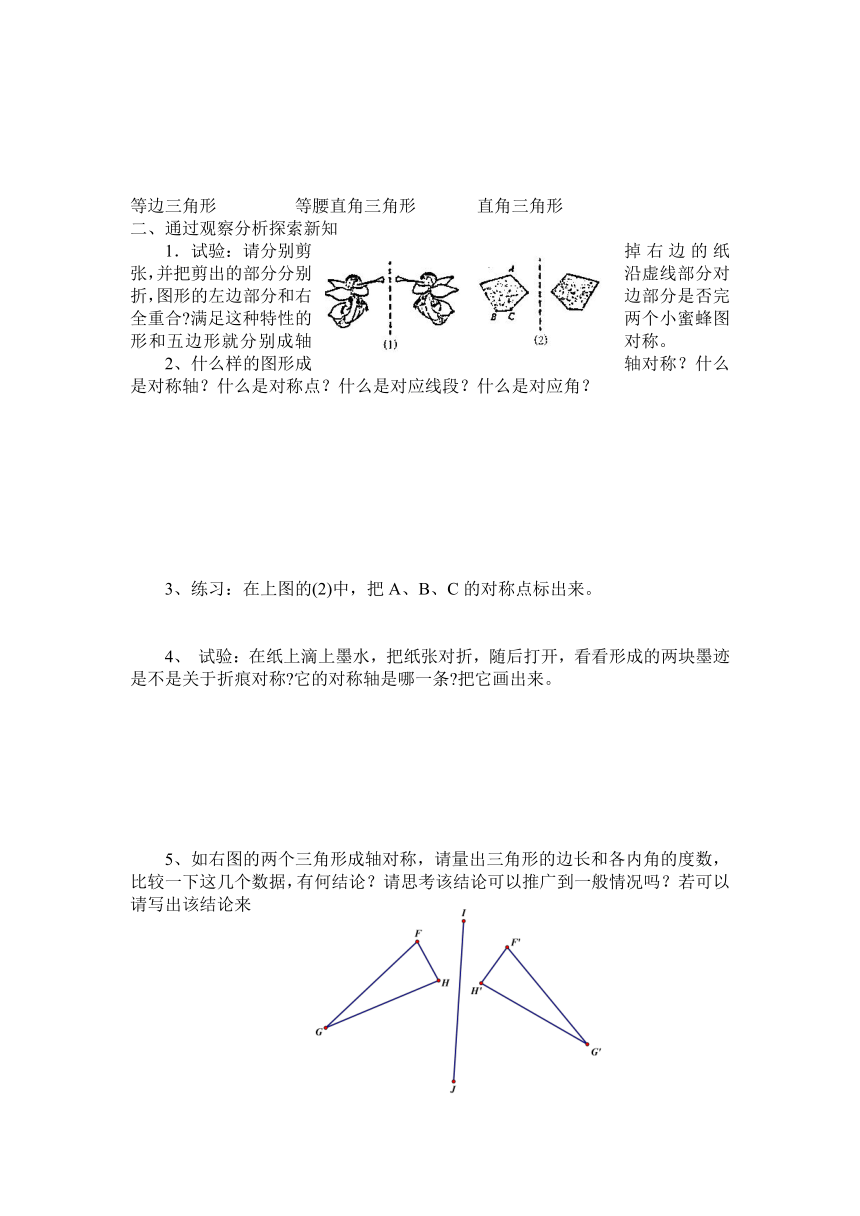
2、请观察下列个三角形,它们都是轴对称图形吗?若是请画出对称轴来
等边三角形 等腰直角三角形 直角三角形
二、通过观察分析探索新知
1.试验:请分别剪掉右边的纸张,并把剪出的部分分别沿虚线部分对折,图形的左边部分和右边部分是否完全重合 满足这种特性的两个小蜜蜂图形和五边形就分别成轴对称。
2、什么样的图形成轴对称?什么是对称轴?什么是对称点?什么是对应线段?什么是对应角?
练习:在上图的(2)中,把A、B、C的对称点标出来。
4、 试验:在纸上滴上墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称 它的对称轴是哪一条 把它画出来。
5、如右图的两个三角形成轴对称,请量出三角形的边长和各内角的度数,比较一下这几个数据,有何结论?请思考该结论可以推广到一般情况吗?若可以请写出该结论来
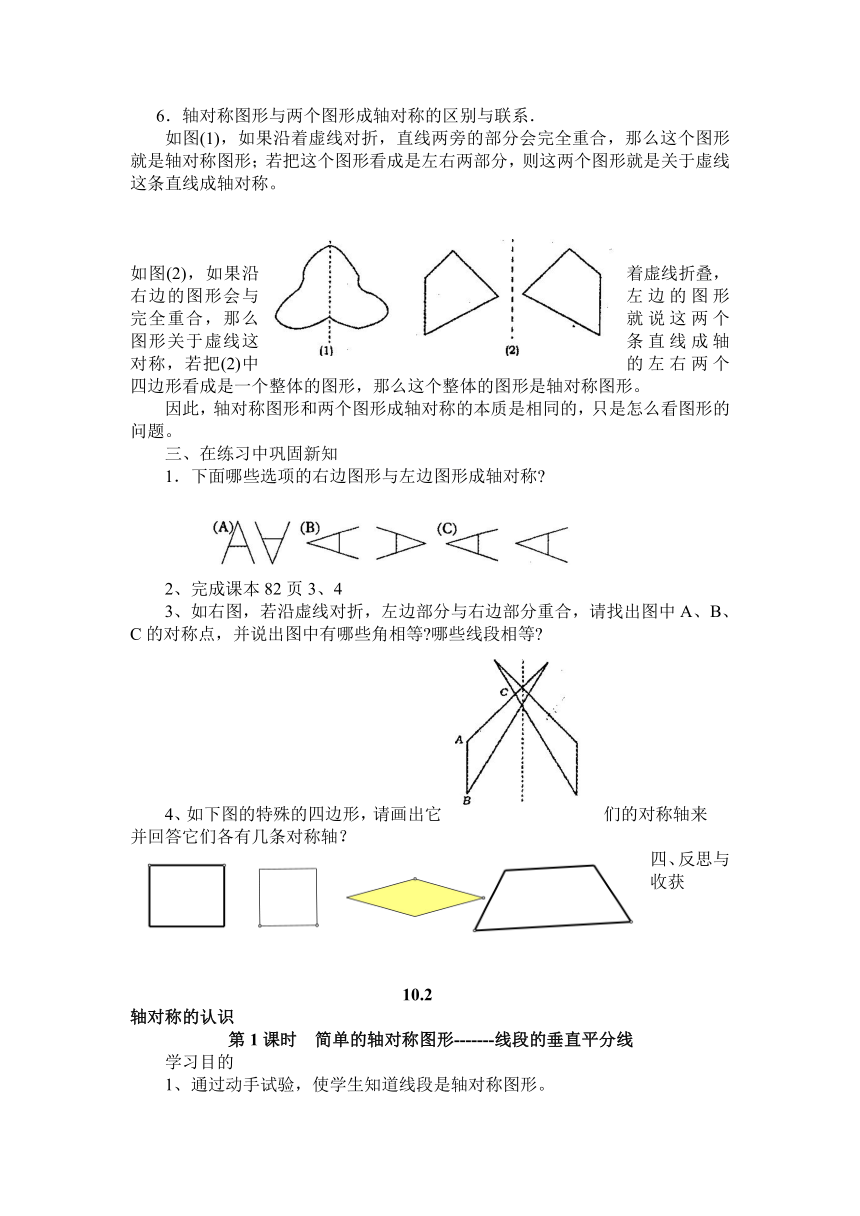
6.轴对称图形与两个图形成轴对称的区别与联系.
如图(1),如果沿着虚线对折,直线两旁的部分会完全重合,那么这个图形就是轴对称图形;若把这个图形看成是左右两部分,则这两个图形就是关于虚线这条直线成轴对称。
如图(2),如果沿着虚线折叠,右边的图形会与左边的图形完全重合,那么就说这两个图形关于虚线这条直线成轴对称,若把(2)中的左右两个四边形看成是一个整体的图形,那么这个整体的图形是轴对称图形。
因此,轴对称图形和两个图形成轴对称的本质是相同的,只是怎么看图形的问题。
三、在练习中巩固新知
1.下面哪些选项的右边图形与左边图形成轴对称
2、完成课本82页3、4
3、如右图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等 哪些线段相等
4、如下图的特殊的四边形,请画出它们的对称轴来
并回答它们各有几条对称轴?
四、反思与收获
轴对称的认识
第1课时 简单的轴对称图形-------线段的垂直平分线
学习目的
1、通过动手试验,使学生知道线段是轴对称图形。
2、掌握线段的垂直子分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。
3、通过线段垂直平分线性质的概括提高分析概括能力
学习重点:线段垂直平分线上的点到线段两端的距离相等。
学习难点:运用线段垂直平分线性质解决问题。
学习过程
一、通过复习感知新知
1.轴对称图形的定义是什么
2.请猜想线段是轴对称图形吗
二、通过实验探索新知
1.认识线段是轴对称图形
试验1:按以下方法,看看线段是否是轴对称图形
在纸上画出线段AB和它的中点O,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合 线段是轴对称图形?
线段的对称轴是哪一条直线呢
2、线段垂直平分线的定义:垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线。如实验中的直线 CD就是线段AB的垂直平分线。
3、线段垂直平分线上性质
实验2:在以上试验的基础上,在直线CD上任意取一点M,连结 MA、MB,而后沿着直线CD折叠,观察MA和MB是否重合 再取一点试试,
实验三:有兴趣的同学请应用几何画板完成以上实验
通过以上实验,请分析概括出你的结论
4、请用几何语言表示出以上结论
三、提高练习巩固新知:
1、完成课本86页1
2、.如右图所示,△ABC中,AC=10,边BA的垂直平分线分别交AC、AB于点D、E,BC=6,求△BCD的周长。
3.如右图所示,DE和DF分别垂直平分线段 AB、BC,请猜想线段AD与线段CD有何关系 为什么
4、如图,AB垂直平分线段CD,垂足为点B,点E、F是AB上的点,CD=40,AB=35,则图中阴影部分的面积是
四、反思与收获.
10.2轴对称的认识(1)
学习目的
通过动手试验,知道角是轴对称图形,其对称轴是角平分线所在的直线,
通过类比设计出实验方法来验证角的对称性
通过类比实验总结出角平分线的性质,并能运用它解决相关问题。
学习重点:角平分线上的点到角两边的距离相等。
学习难点:运用角平分线性质解决问题。
学习过程
认真阅读课本86页并解决一下问题
一、通过复习引入新知
1、线段的对称轴是什么?它有什么样的性质?
2、线段垂直平分线的性质是如何得来的?
3、请猜想角的对称性?你能否类比线段对称性的实验方法设计一个实验角的对称性的实验?
二、通过实验探究新知新课
1、你的实验方法是:
2、你的实验结论是:
(1)
(2)
(3)你的结论用几何语言表示为
三、提高练习巩固新知:
1、完成课本86页练习2、3、4
2、如图,AD平分∠BAC,∠C=90°,DE⊥ AB,那么(1)DE和DC相等吗 为什么 (2)AE和AC相等吗 为什么
3、如图,在△ABC中,用直尺、量角器画∠A、∠B、∠C的平分线,看看三条角平分线有什么关系
4、如下图所示,在△ABC中,∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,DE=5, 求CD的长及∠A的度数
5、如上图(2),BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,求 P点到直线AB的距离。
四、反思与收获
10.2轴对称的认识(3)
学习目的
通过画图形的对称轴,发现用“连结对称点的线段被对称轴垂直平分”这一结论来验证一个图形是不是轴对称图形,
熟练画出轴对称图形的对称轴。
学习重点:画轴对称图形的对称轴。
学习难点:归纳总结画轴对称图形对称轴的方法。
学习过程
仔细阅读课本86-88页,并解决以下问题
一、通过复习感知新知
1.轴对称图形以及它的对称点是怎么定义的
2.看以下两个图形是否是轴对称图形 你能否画出它的对称轴
二、通过操作探究新知
1、试画出课本86页图10.2.5中两个图形的对称轴
2、试着画出下边两个图形的对称轴。
用折叠的方法检验所画的对称轴是否准确,如果准确的话,请你总结方法,并说出如何判断对称轴的位置。
3、对称轴的画法
首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
4、请写出轴对称图形的对称轴的结论
三、在应用中巩固新知
1、完成课本87页做一做
2、完成课本88页练习1、2、3
3、画出以下图形的对称轴
四、反思与收获
10.2轴对称的认识(4)
学习目的
1.通过在个点图中画轴对称图形体会画轴对称图形的方法
2、通过完成做一做中画最简单轴对称图形的方法进一步感知画轴对称图形的方法
3、通过阅读课本例题规范画轴对称图形的方法。体会画轴对称图形的关键实际上是画一些关键点的对称点,然后顺次连结就得到所要画的轴对称图形
4、通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。
学习重点、难点:能准确地画出轴对称图形。
学习过程
一、通过复习感知新知
1.什么是轴对称图形
2.请你标出图中,A、B、C三点的对称点。
A
B
C
二、在操作中探究新知
操作1.请尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
(1)你可以通过什么方法来验证你画的是否正确
(2)和其他同学比较一下,你的方法是最简单的吗
在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形吗
操作2.完成课本89页做一做
画好之后,你可以通过什么方法来验证一下A和 A′是否关于直线l对称
操作3、已知△ABC,直线l,画出△ABC关于直线l的对称图形。
(1)本题与上面的那些图比较有什么相同点和不同点
(2)你能否从上面的那些图的画法中得到启示,帮助你解决本题
A
B C
由以上操作可知:如果图形是由直线、线段或射线组成时,那么画出它关于某一条直线对称的图形时,只要画出图形中的特殊点(如线段的中点,角的顶点等)的对称点,然后连结对称点,就可以画出关于这条直线的对称图形。
三、在练习中巩固新知
1、 P90练习第1、2题。
2、P93习题1、2
3、如图画出一直三角形关于直线对称的图形来。观察你所画出的图形你能发现什么新的结论吗?
四、反思与收获
10.2轴对称的认识(5)
学习目的
1.学会设计简单的轴对称图案。
2.能够欣赏现实生活中的轴对称图形。
学习重点:利用对称轴进行图案设计。
学习难点;寻找对称轴以及如何利用对称轴作轴对称图形。
学习过程
一、通过复习引入
1.如图(1),请画出△ABC的关于直线l对称的图形。
2.如图(2),等边△ABC是轴对称图形吗 如果是,它有几条对称轴 画画试试看。
二、在操作中探究新知
在日常生活中,我们可以看到丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中往往有许多轴对称图形。请同学们欣赏P91四个装饰图案。
如图(3)是一个轴对称图形。
1.有多少条对称轴呢
2.可以利用轴对称性来画出它吗
请思考设计该图形的基本方案,对比以下步骤修改完善自己的方案
3、 请在下页正方形中,按以下5个步骤一起来画。
(1)在正方形纸片上画出四条对称轴。
(2)在其中一个三角形中,如图,画出图形形状的基本线条。(注意:不同的线条最终会得到不同的图案,你可以自己设计线条,而不必和书上一样。)
(3)按照其中一条斜的对称轴画出(2)中图形的对称图形。
(4)按照另一条斜的对称轴画出(3)中图形的对称图形。
(5)按照水平(或垂直)对称画出(4)中图形的对称图形,即得到图(3)中的图。
在图案上涂上你喜欢的颜色,擦掉其他的线条,轴对称的图案就完成了。
(6)思考:如何快速画出轴对称图案?
首先要画出对称轴,其次要画出图形形状的部分线条,然后根据对称性画出对称图形。
(7)你能否用几何画板快速地画出上述图案来?
4、如何用几何画板画出你设计的轴对称图形?请试一试。能否把你设计的图形展示给大家。请谈一下自己的收获
四、反思与收获
等腰三角形(1)
学习目的
1.通过学习了解等腰三角形的有关概念,掌握等腰三角形的性质。
2.通过探索等腰三角形的性质,进一步经历观察、实验、推理、交流等活动。
学习重点:等腰三角形等边对等角性质。
学习难点:通过操作,如何观察、分析、归纳得出等腰三角形性质。
学习过程
一、通过复习引入新课
1.在练习本上画一个等腰三角形,标出字母,回答什么样的三角形是等腰三角形 并指出等腰△ABC的腰、顶角、底角
2.日常生活中,哪些物体具有等腰三角形的形象
二、通过操作探究新知
1、实验。
请做一张等腰三角形的半透明纸片,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD,如图(2)所示,你能发现什么现象吗 请你尽可能多的写出结论。
2、请认真观察、思考、总结,可得到哪些结论?该结论如何表示成“如果……..那么……”的形式.
3、请用几何语言表示你的结论:
三、在练习中巩固新知
1、填空:在△ABC中,AB=AC,D在BC上,
如果AD⊥BC,那么∠BAD=∠______ ,BD=_______
如果∠BAD=∠CAD,那么AD⊥_____ ,BD=______
如果BD=CD,那么∠BAD=∠_______ ,AD⊥______
2、已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
3、已知:在△ABC中,AB=AC,∠A=80°,求∠B和∠C的度数。
4、练习1、2、3
5、如图,在△ABC中,AB=AC,AC⊥BD于点D,∠A=40°,求∠DBC的度数
6、如图,在△ABC中,AB=AC,DE是线段AB的垂直平分线。
(1)若∠A=40°,求∠C的度数
(2)若AB=12,BC=8,求△DBC的周长
四、反思与收获
等腰三角形(2)
学习目的
1.通过复习学会熟练运用等腰三角形的性质求等腰三角形内角的角度。
2.通过探究掌握等边三角形的性质。
学习重点,等腰三角形的性质及其应用。
学习难点:会简洁的逻辑推理。
学习过程
一、通过复习巩固等腰三角形的性质
1.叙述等腰三角形的性质,并回忆它是怎么得到的
等腰三角形的两个 相等,也可以简称“ ”。把等腰三角形对折,折叠两部分是互相重合的,即AB与AC重合,点B与点 C重合,线段BD与CD也重合,所以∠B=∠C。
等腰三角形的 互相重合,简称“三线合一”。由于AD为等腰三角形的对称轴,所以BD= CD,AD为底边上的中线;∠BAD=∠CAD,AD为顶角平分线,∠ADB=∠ADC=90°,AD又为底边上的高,因此“三线合一”。
2.若等腰三角形的两边长为3和4,则其周长为多少
二、通过实验探究新知
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。我们把三条边都相等的三角形叫做 三角形。等边三角形也称为正三角形。
等边三角形具有什么性质呢
请同学们画一个等边三角形,用量角器
量出各个内角的度数,并提出猜想。
你能否用已知的知识,通过推理得到你的猜想是正确的
3.上面的条件和结论如何叙述
等边三角形的 都相等,并且每一个角都等于 。
4、等边三角形是轴对称图形吗 如果是,有几条对称轴
三、在练习中巩固新知
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合( )
b.有一个角是60°的等腰三角形,其它两个内角也为60°( )
2.如图(2),在△ABC中,已知AB=AC,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。
3、如图,△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
4、已知AD是等腰△ABC的腰BC边上的高,∠DAB=60°,求这个三角形各内角的度数
四、反思与收获
等腰三角形(3)
学习目的
1.通过操作探索一个三角形是等腰三角形的条件。
2.能利用一个三角形是等腰三角形的条件,正确判断某个三角形是否为等腰三角形。
学习重点:让学生掌握一个三角形是等腰三角形的条件和正确应用。
学习难点:一个三角形是等腰三角形的条件的正确文字叙述。
一、通过复习引入新知
1、 等腰三角形具有哪些性质
2、等腰三角形的性质是怎么得到的
二、通过操作探究新知
1、对于一个三角形,怎样识别它是不是等腰三角形呢
2、等腰三角形的判定
请拿出一张半透明纸,做一个实验,按以下方法进行操作:
(1).在半透明纸上画一条线段BC。
(2).以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的角,两角终边的交点为A。
(3).用刻度尺找出BC的中点D,连接AD,然后沿AD对折。
问题1:AB与AC是否重合
问题2:本实验的条件与结论如何用文字语言加以叙述
问题3:本实验的条件与结论如何用几何语言加以叙述
问题4:三个角都是60°的三角形是等边三角形吗 你能说明理由吗
3.等腰直角三角形的有关概念:
你认为什么样的三角形为等腰直角三角形?
问题5:你能说出等腰直角三角形各角的大小吗
问题6:请你画一个等腰直角三角形,使∠C=90°,CD是底边上的高,数一数图中共有几个等腰直角三角形
三、在练习中巩固新知
1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
2.在△ABC中,已知AB=AC,BE、CF分别是∠ABC、
∠ACB的平分线,交于点O, 请猜想△OBC的形状,并说出理由
3、如图,△ABC是等边三角形,BD是△ABC的高,延长BC到点E,使CE=CD,试判断△BDE的形状,并说明理由
4、等腰三角形一腰上的高与另一腰的夹角为40°,求这个等腰三角形的底角的度数。
四、反思与收获
