幂的乘方
图片预览






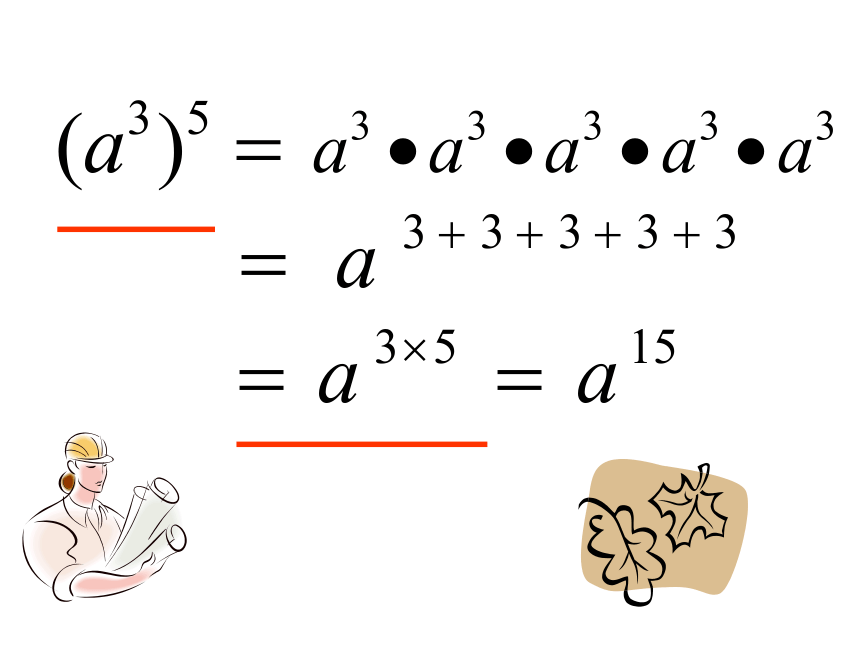
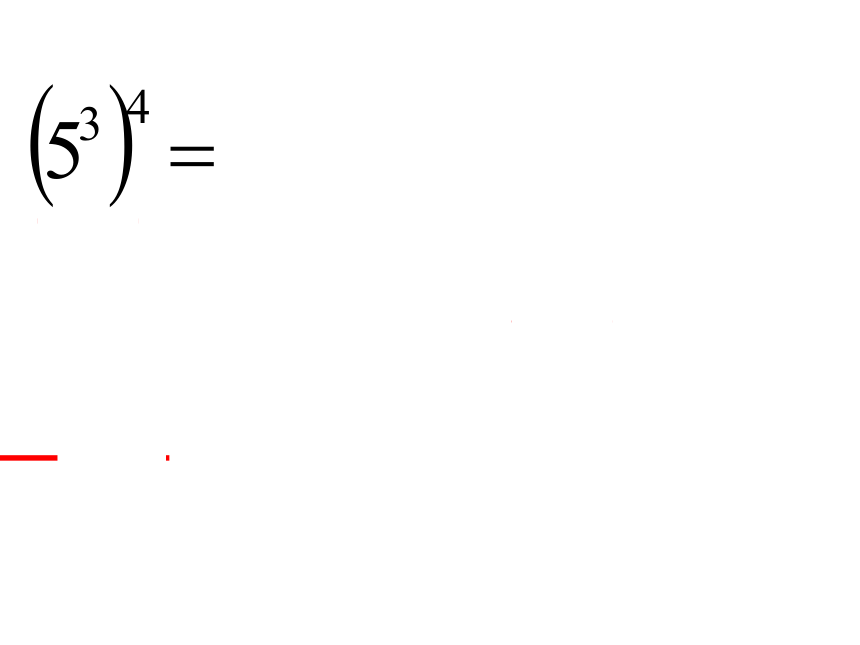




文档简介
课件31张PPT。11.2 幂的乘方七年级下(青岛版)知识与能力教学目标 1.了解幂的乘方的运算性质,会进行幂的乘方运算;
2.能利用幂的乘方的性质解决一些实际问题. 表示___个___相乘.
表示___个___相乘.
表示___个___相乘.
表示___个___相乘.4343a3探索 地球可以近似地看做是球体,地球的半径约为6.37×103 km,它的体积大约是多少立方千米? 那么, (103)3 =?
这种运算有什么特征?=探索交流你知道(103)3等于多少吗?(103)3=103×103×103=103+3+3=103×3=109(根据 ).(根据 ).同底数幂的乘法乘方的意义(根据乘法的意义).探究新知试一试:
你会计算探究新知观察计算结果,猜想对于任意底数a与任意正整数m,n,一般地,我们有即幂的乘方,底数不变,指数相乘.知识要点幂的乘方法则:其中m , n都是正整数想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?幂的乘方法则:其中m , n都是正整数同底数幂的乘法法则:底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m , n都是正整数落实基础 例1 计算:
(102)3 ; (2) (b5)5 ;
(an)3; (4) -(x2)m ;
(5) (y2)3 · y ; 口答(1)(5m2)3 (2)(-xy2)3
(3)(-ab)5 (4)(x2y3)4
(5)(2×103)2 (6)(-0.5a3y4)3
(7)[(-3)3]2 (8)比较不同(1) [(-5)2]3=
(2)[(-52)]3=
(3)[(-x)3]5=
(4)[(x-y)3]2=
(5) -(x3)2=
(6)(x3)4 · x2=56-56-x15(x-y)6-x6x14抢答例2 计算:解:原式=解:原式=(3)落实基础2. 计算:
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 . 随堂练习:
1. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .⑴ a12 =(a3)(4) =(a2)(6 )
=a3 a(9 )=( )3 =( )4(4) 32﹒9m =3( )(2) y3n =3, y9n = .
(3) (a2)m+1 = .
拓广
练习课堂小结幂的乘方即幂的乘方,底数不变,指数相乘.2.若 ,则n=_______.3.若 ,求 的值.4.若 ,求 的值.5.已知 ,求 的值.48729361.计算:练一练参考练习 1、填空:________________( )( )________________2、选择题A、n是奇数 B、n是偶数 C、n是正整数 D、n是整数[2]下列计算中,正确的有( )。 A、0个 B、1个 C、2个 D、4个 [3]若 ( )。 A、11 B、18 C、30 D、33 3、计算: 练习(1)xn·xn -2·(-x)3
(2)[(-a2b)3]3
(3)(-x2y)3·(-xy)2
(4)(2x)2·x4
(5)(-2x)3·(-xy2)2综合训练例2、计算:
(1)(-0.125)2006·82006 (2)[(m+n)2·(a -b)3]2
(3)(-2a2b)3+(a3)2·b3,其中a=1,b= -2(1)若2n=3,2m=2,求23n+2m的值;
(2)已知323×162=2x-1,求x的值;
(3)已知 ,求
a2008b2008的值。拓展提高1.(-3/7) 105× (9/49) -52 =________;
2.如果(x2y)a×(xybz)3×(y2z3)2
=x5y8zc+1,求a、b、c的值.
3.若2a+3×3a+3=36a-2,求a=____.-3/7a=1;b=1;c=87随堂练习
2.能利用幂的乘方的性质解决一些实际问题. 表示___个___相乘.
表示___个___相乘.
表示___个___相乘.
表示___个___相乘.4343a3探索 地球可以近似地看做是球体,地球的半径约为6.37×103 km,它的体积大约是多少立方千米? 那么, (103)3 =?
这种运算有什么特征?=探索交流你知道(103)3等于多少吗?(103)3=103×103×103=103+3+3=103×3=109(根据 ).(根据 ).同底数幂的乘法乘方的意义(根据乘法的意义).探究新知试一试:
你会计算探究新知观察计算结果,猜想对于任意底数a与任意正整数m,n,一般地,我们有即幂的乘方,底数不变,指数相乘.知识要点幂的乘方法则:其中m , n都是正整数想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?幂的乘方法则:其中m , n都是正整数同底数幂的乘法法则:底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m , n都是正整数落实基础 例1 计算:
(102)3 ; (2) (b5)5 ;
(an)3; (4) -(x2)m ;
(5) (y2)3 · y ; 口答(1)(5m2)3 (2)(-xy2)3
(3)(-ab)5 (4)(x2y3)4
(5)(2×103)2 (6)(-0.5a3y4)3
(7)[(-3)3]2 (8)比较不同(1) [(-5)2]3=
(2)[(-52)]3=
(3)[(-x)3]5=
(4)[(x-y)3]2=
(5) -(x3)2=
(6)(x3)4 · x2=56-56-x15(x-y)6-x6x14抢答例2 计算:解:原式=解:原式=(3)落实基础2. 计算:
(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 . 随堂练习:
1. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .⑴ a12 =(a3)(4) =(a2)(6 )
=a3 a(9 )=( )3 =( )4(4) 32﹒9m =3( )(2) y3n =3, y9n = .
(3) (a2)m+1 = .
拓广
练习课堂小结幂的乘方即幂的乘方,底数不变,指数相乘.2.若 ,则n=_______.3.若 ,求 的值.4.若 ,求 的值.5.已知 ,求 的值.48729361.计算:练一练参考练习 1、填空:________________( )( )________________2、选择题A、n是奇数 B、n是偶数 C、n是正整数 D、n是整数[2]下列计算中,正确的有( )。 A、0个 B、1个 C、2个 D、4个 [3]若 ( )。 A、11 B、18 C、30 D、33 3、计算: 练习(1)xn·xn -2·(-x)3
(2)[(-a2b)3]3
(3)(-x2y)3·(-xy)2
(4)(2x)2·x4
(5)(-2x)3·(-xy2)2综合训练例2、计算:
(1)(-0.125)2006·82006 (2)[(m+n)2·(a -b)3]2
(3)(-2a2b)3+(a3)2·b3,其中a=1,b= -2(1)若2n=3,2m=2,求23n+2m的值;
(2)已知323×162=2x-1,求x的值;
(3)已知 ,求
a2008b2008的值。拓展提高1.(-3/7) 105× (9/49) -52 =________;
2.如果(x2y)a×(xybz)3×(y2z3)2
=x5y8zc+1,求a、b、c的值.
3.若2a+3×3a+3=36a-2,求a=____.-3/7a=1;b=1;c=87随堂练习
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
