人教版八年级数学上册11.2.1《三角形的内角》教学设计
文档属性
| 名称 | 人教版八年级数学上册11.2.1《三角形的内角》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 09:51:02 | ||
图片预览

文档简介
11.2.1三角形的内角(1)
【教学目标】
1、理解三角形的内角和定理与证明过程,能灵活运用三角形的内角和定理解决简单的与三角形中有关角的计算和证明问题。
2、了解辅助线的作用,能规范地书写简单的推理过程。
3、经历猜想、实验、证明、归纳等活动,感受数学思维的严谨性,渗透转化思想。
【教学重点】探索三角形内角和定理的证明过程及其简单的应用。
【教学难点】在三角形内角和定理的证明过程中正确添加辅助线。
【教学过程】
一、创设情境 导入新课
问题1:任意一个三角形的内角和等于多少度 你还记得这个结论的探索过程吗
度量、剪拼(有误差)。
问题2:有没有更严谨的办法进行验证
通过推理的方法去证明
问题3:在已学知识中有什么方法可以得到180°
一个平角是180°;两直线平行时,同旁内角的和是180°。
问题4:从刚才拼角的过程你能想出证明的办法吗
拼角的实质是移动角,如果不实际移动角,你有什么方法可达到同样的效果
追问:想到用平角或平行,但没有平角或平行怎么办
添加辅助线思路:构造平角或平行线.为了证明的需要,在原来的图形上添画的线叫做辅助线。做辅助线是几何证明过程中常用到的方法。辅助线通常画成虚线。
添加辅助线的实质是通过平行线来移动角——构造平行线间的内错角、同位角、同旁内角,构造平角。
二、合作交流 解读探究
已知△ABC,求证:∠A+∠B+∠C=180 °. (学生讲解或老师点评)
(在证明中,当原来的条件不够时,可添加辅助线,从而构造新图形,形成新关系,找到已知与未知桥梁,把问题转化成自己已经会解的情况,这是解决问题常用方法的方法之一,辅助线通常画成虚线。)
三种推理方法1:(作平行线,构造内错角、平角)
过A点作DE∥BC
∵DE∥BC
∴∠DAB=∠B,∠EAC=∠C
(两直线平行,内错角相等)
∵∠DAB+∠BAC+∠EAC=∠DAE=180°
∴∠BAC+∠B+∠C=180°(等量代换)
方法2:(作平行线,构造内错角、同位角、平角)
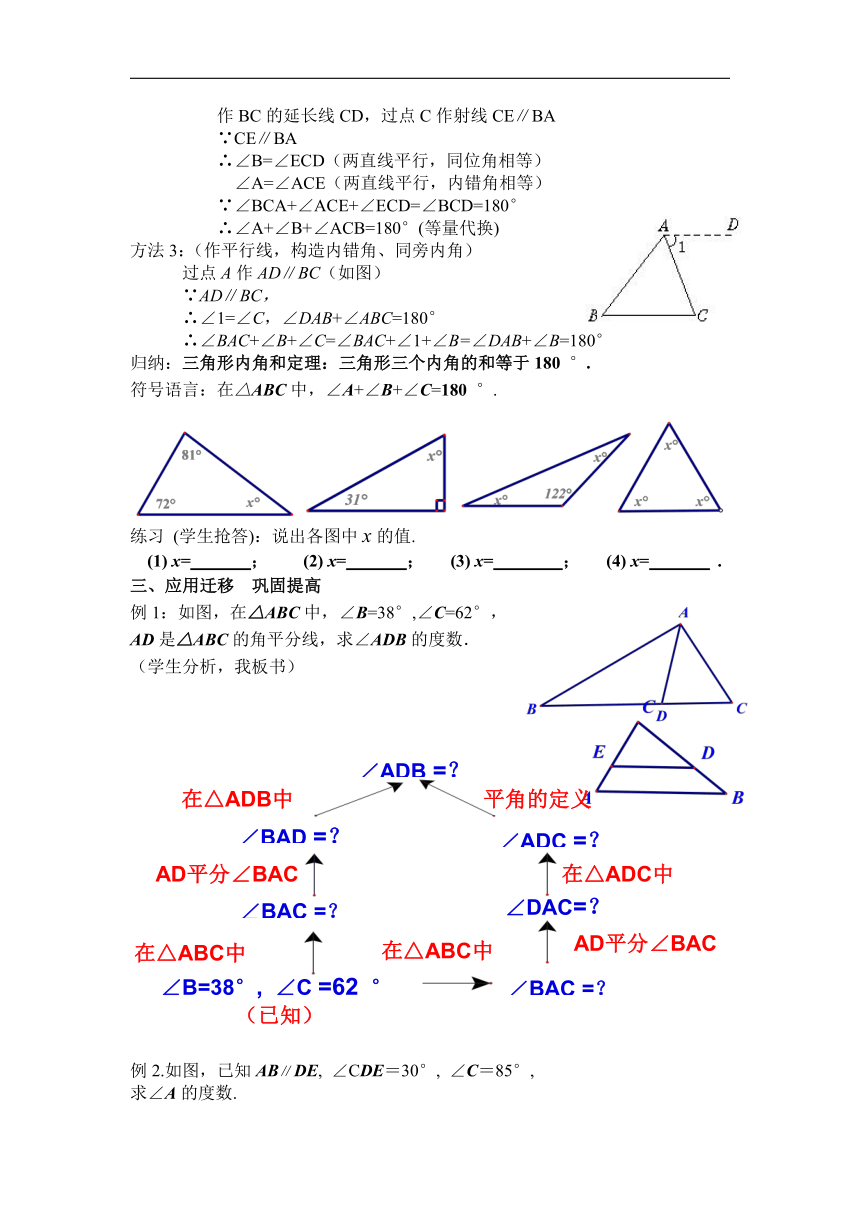
作BC的延长线CD,过点C作射线CE∥BA
∵CE∥BA
∴∠B=∠ECD(两直线平行,同位角相等)
∠A=∠ACE(两直线平行,内错角相等)
∵∠BCA+∠ACE+∠ECD=∠BCD=180°
∴∠A+∠B+∠ACB=180°(等量代换)
方法3:(作平行线,构造内错角、同旁内角)
过点A作AD∥BC(如图)
∵AD∥BC,
∴∠1=∠C,∠DAB+∠ABC=180°
∴∠BAC+∠B+∠C=∠BAC+∠1+∠B=∠DAB+∠B=180°
归纳:三角形内角和定理:三角形三个内角的和等于180 °.
符号语言:在△ABC中,∠A+∠B+∠C=180 °.
练习 (学生抢答):说出各图中x的值.
(1) x= ; (2) x= ; (3) x= ; (4) x= .
三、应用迁移 巩固提高
例1:如图,在△ABC中,∠B=38°,∠C=62°,AD是△ABC的角平分线,求∠ADB的度数.
(学生分析,我板书)
例2.如图,已知AB∥DE, ∠CDE=30°, ∠C=85°,
求∠A的度数.
(学生甲、乙讲解)
变式:如图,已知∠A=30°,∠B=70°, ∠CDE=25°,
求∠CED的度数.
(学生板演)
练习:如图,△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.
(投影)
四、总结反思 拓展升华
通过本节课的学习你有什么收获
数学知识:三角形内角和定理的证明及简单应用
数学思想:转化思想
五、课堂检测
1. 已知△ABC中,∠ABC=∠C=2∠A , 则∠C的度数______.
2. 已知△ABC中, ∠C=90°, ∠A-∠B=30°,则∠B =_____.
3. 如图,已知CD是△ABC的高, ∠ACB=90°, ∠A=60°,则∠BCD =_________.
4.如图,∠A+∠B+∠C+∠D+∠E =_________.
5.如图,△ABC的角平分线BD与CD相交于点D,
(1)若∠A=100°,则∠BDC = ______;
(2)若∠A=80°,则∠BDC = ______;
(3)猜想:∠BDC与∠A有怎样的数量关系?请说明理由.
思考:一个三角形最多有几个直角?为什么?最多有几个钝角? 一个三角形最多有几个锐角?最少有几个锐角?你能否利用三角形的内角和,求出四边形、五边形的内角和?
六、板书设计:
11.2.1 三角形内角和定理(1)
三角形内角和定理:三角形三个内角的和等于180°
学生展示的拼图方法:
例1
例2变式
A
B
C
D
E
∠ADB =?
在△ADB中
平角的定义
∠ADC =?
∠BAD =?
AD平分∠BAC
在△ADC中
∠DAC=?
∠BAC =?
在△ABC中
AD平分∠BAC
∠BAC =?
在△ABC中
∠B=38°, ∠C =62 °
(已知)
【教学目标】
1、理解三角形的内角和定理与证明过程,能灵活运用三角形的内角和定理解决简单的与三角形中有关角的计算和证明问题。
2、了解辅助线的作用,能规范地书写简单的推理过程。
3、经历猜想、实验、证明、归纳等活动,感受数学思维的严谨性,渗透转化思想。
【教学重点】探索三角形内角和定理的证明过程及其简单的应用。
【教学难点】在三角形内角和定理的证明过程中正确添加辅助线。
【教学过程】
一、创设情境 导入新课
问题1:任意一个三角形的内角和等于多少度 你还记得这个结论的探索过程吗
度量、剪拼(有误差)。
问题2:有没有更严谨的办法进行验证
通过推理的方法去证明
问题3:在已学知识中有什么方法可以得到180°
一个平角是180°;两直线平行时,同旁内角的和是180°。
问题4:从刚才拼角的过程你能想出证明的办法吗
拼角的实质是移动角,如果不实际移动角,你有什么方法可达到同样的效果
追问:想到用平角或平行,但没有平角或平行怎么办
添加辅助线思路:构造平角或平行线.为了证明的需要,在原来的图形上添画的线叫做辅助线。做辅助线是几何证明过程中常用到的方法。辅助线通常画成虚线。
添加辅助线的实质是通过平行线来移动角——构造平行线间的内错角、同位角、同旁内角,构造平角。
二、合作交流 解读探究
已知△ABC,求证:∠A+∠B+∠C=180 °. (学生讲解或老师点评)
(在证明中,当原来的条件不够时,可添加辅助线,从而构造新图形,形成新关系,找到已知与未知桥梁,把问题转化成自己已经会解的情况,这是解决问题常用方法的方法之一,辅助线通常画成虚线。)
三种推理方法1:(作平行线,构造内错角、平角)
过A点作DE∥BC
∵DE∥BC
∴∠DAB=∠B,∠EAC=∠C
(两直线平行,内错角相等)
∵∠DAB+∠BAC+∠EAC=∠DAE=180°
∴∠BAC+∠B+∠C=180°(等量代换)
方法2:(作平行线,构造内错角、同位角、平角)
作BC的延长线CD,过点C作射线CE∥BA
∵CE∥BA
∴∠B=∠ECD(两直线平行,同位角相等)
∠A=∠ACE(两直线平行,内错角相等)
∵∠BCA+∠ACE+∠ECD=∠BCD=180°
∴∠A+∠B+∠ACB=180°(等量代换)
方法3:(作平行线,构造内错角、同旁内角)
过点A作AD∥BC(如图)
∵AD∥BC,
∴∠1=∠C,∠DAB+∠ABC=180°
∴∠BAC+∠B+∠C=∠BAC+∠1+∠B=∠DAB+∠B=180°
归纳:三角形内角和定理:三角形三个内角的和等于180 °.
符号语言:在△ABC中,∠A+∠B+∠C=180 °.
练习 (学生抢答):说出各图中x的值.
(1) x= ; (2) x= ; (3) x= ; (4) x= .
三、应用迁移 巩固提高
例1:如图,在△ABC中,∠B=38°,∠C=62°,AD是△ABC的角平分线,求∠ADB的度数.
(学生分析,我板书)
例2.如图,已知AB∥DE, ∠CDE=30°, ∠C=85°,
求∠A的度数.
(学生甲、乙讲解)
变式:如图,已知∠A=30°,∠B=70°, ∠CDE=25°,
求∠CED的度数.
(学生板演)
练习:如图,△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.
(投影)
四、总结反思 拓展升华
通过本节课的学习你有什么收获
数学知识:三角形内角和定理的证明及简单应用
数学思想:转化思想
五、课堂检测
1. 已知△ABC中,∠ABC=∠C=2∠A , 则∠C的度数______.
2. 已知△ABC中, ∠C=90°, ∠A-∠B=30°,则∠B =_____.
3. 如图,已知CD是△ABC的高, ∠ACB=90°, ∠A=60°,则∠BCD =_________.
4.如图,∠A+∠B+∠C+∠D+∠E =_________.
5.如图,△ABC的角平分线BD与CD相交于点D,
(1)若∠A=100°,则∠BDC = ______;
(2)若∠A=80°,则∠BDC = ______;
(3)猜想:∠BDC与∠A有怎样的数量关系?请说明理由.
思考:一个三角形最多有几个直角?为什么?最多有几个钝角? 一个三角形最多有几个锐角?最少有几个锐角?你能否利用三角形的内角和,求出四边形、五边形的内角和?
六、板书设计:
11.2.1 三角形内角和定理(1)
三角形内角和定理:三角形三个内角的和等于180°
学生展示的拼图方法:
例1
例2变式
A
B
C
D
E
∠ADB =?
在△ADB中
平角的定义
∠ADC =?
∠BAD =?
AD平分∠BAC
在△ADC中
∠DAC=?
∠BAC =?
在△ABC中
AD平分∠BAC
∠BAC =?
在△ABC中
∠B=38°, ∠C =62 °
(已知)
