人教版八年级数学上册11.3《﹡数学活动 平面镶嵌》教学设计(表格式)
文档属性
| 名称 | 人教版八年级数学上册11.3《﹡数学活动 平面镶嵌》教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 391.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 09:53:32 | ||
图片预览


文档简介
《平面镶嵌》教学设计表
课名 《平面镶嵌》 教师姓名
学科(版本) 人教版数学 章节 上册十一章 数学活动课
学时 第一课时 年级 八年级
一、教学目标 1.知识与技能 (1)通过对平面图形镶嵌问题的探究与解决(当然不一定能完全解决)的过程,加深对正多边形的有关概念、性质的理解; (2)经历实验、探究的学习过程,掌握同一种或两种正多边形镶嵌的问题以及任意三角形或四边形的镶嵌. (3)任意的三角形或四边形的镶嵌. 2.过程与方法 在探究的过程中让学生了解数学知识在实际生产生活中的应用,培养学生应用数学解决实问题的意识和能力; 3.情感态度与价值观 经历探究学习优化学生的思维品质,培养学生发散性思维能力及由特殊到一般的归纳能力;通过合作学习,培养学生团结协作的团队精神.
二、学习者分析 对于八年级学生而言,他们刚刚学习了多边形内角和与正多边形的相关概念,所以学生介于对于多边形的内角度数的了解来学习平面图形的镶嵌.教学的主题是把日常生活中的铺地砖的问题抽象为数学中的平面图形的镶嵌问题. 并利用平面图形镶嵌的知识应用于生活中去. 本节课设计的理论支撑点是建构主义的学习理论,这种理论认为学生的学习不是被动的接受,而是一种主动的探究与建构,认为各个个体对知识的理解随个人的经验、经历的不同而不同. 根据这一理论,教师在教学设计中充分考虑到学生的差异,设计一系列的探究活动是从简单到复杂,从特殊到一般,教学中采用小组合作学习的方式,以学生为主体,让学生自己发现问题、思考问题、解决问题,拓展问题.整个课堂中全体学生都参与进来,学生真正的作为自己学习的主人,教师只是引领者和指导者.
三、教学重难点分析及解决措施 教学重点:1.探究边长相等的同一种正多边形或两种正多边形的镶嵌. 2.任意的三角形或四边形的镶嵌. 教学难点:探究边长相等同一种正多边形或两种正多边形的镶嵌的过程. 解决重难点的措施: 1.通过网络和交互式电子白板的“置顶”功能,展示生活中的各种贴地砖和墙砖的图片,带领学生进入学习情境,激发学生的学习兴趣,通过“感知概念—初次探究—再次探究—延伸拓展”四个层次递进的环节,引导学生对平面图形镶嵌活动的探究. 2.在探究边长相等的一种正多边形的镶嵌环节时,利用交互式电子白板的“拖动副本”、“限制器”和数学工具的功能让学生在白板上动手操作探究,同时其余学生利用学具进行动手操作探究.
四、教学设计
教学环节 环节目标 教学内容 学生活动 媒体作用及分析
一、展示情景,给出概念 结合图片,让学生初步感知从贴地砖的生活现象中蕴含着数学道理,了解从一个顶点处围成360度的角就可以无缝隙,无重叠,从而引出平面图形镶嵌的概念. 1.观察图片,感知表象 展示图片,感知镶嵌. 提出问题:你觉得贴地砖的过程中需要注意什么?蕴含着哪些数学知识? 2.回归数学,给出概念 平面图形的镶嵌:用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称平面图形的镶嵌. 生观察图片,获得感知. 生:图片中的地砖都是铺得平平的,地砖的大小是一样的,顶点在一个点处. 生:这些地砖之间没有一点空隙,也没有重叠在一起. 全体生齐声朗读概念,了解平面图形的镶嵌. 利用电子白板的后置的功能,逐步的显示图片,从而引起学生注意,激发学生的学习兴趣,今儿引入本节课—平面图形的镶嵌. 利用电子白板的书写功能,通过画直线和方框强调概念中的相关语句,加深学生对平面图形镶嵌的理解.
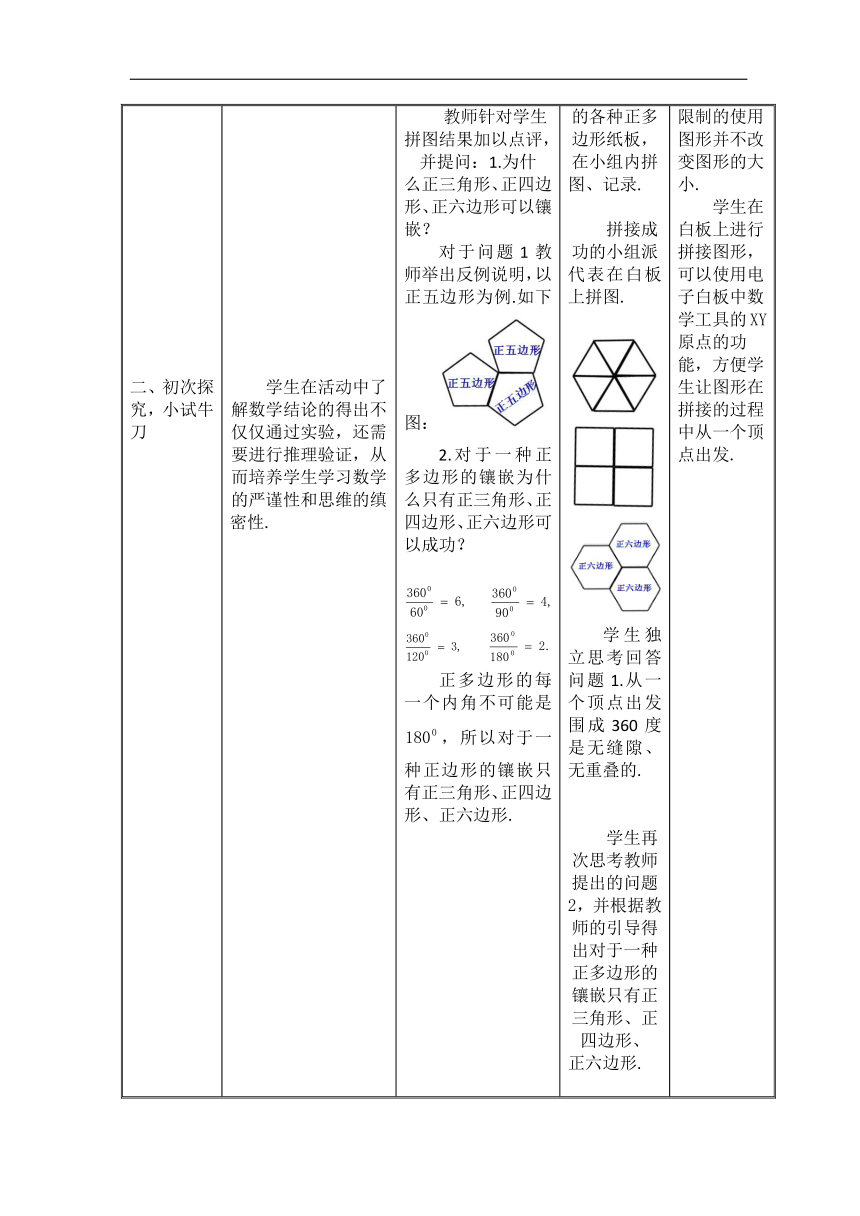
二、初次探究,小试牛 刀 培养学生合作探 究的能力. 学生在活动中了解数学结论的得出不仅仅通过实验,还需要进行推理验证,从而培养学生学习数学的严谨性和思维的缜 密性. 探究:限用同一种正多边形进行平面镶嵌,哪几种正多 边形可以? 教师针对学生拼图结果加以点评,并提问:1.为什 么正三角形、正四边形、正六边形可以镶 嵌? 对于问题1教师举出反例说明,以正五边形为例.如下图: 2.对于一种正多边形的镶嵌为什么只有正三角形、正四边形、正六边形可以成功? 正多边形的每一个内角不可能是,所以对于一种正边形的镶嵌只有正三角形、正四边形、正六边形. 同学们拿出准备好的各种正多边形纸板,在小组内拼 图、记录. 拼接成功的小组派 代表在白板上拼图. 学生独立思考回答问题1.从一个顶点出发围成360度是无缝隙、无重叠的. 学生再次思考教师提出的问题2,并根据教师的引导得出对于一种正多边形的镶嵌只有正三角形、正四边形、 正六边形. 利用电子白板中拖动副本和限制器的功能,可以无限制的使用图形并不改变图形的大小. 学生在白板上进行拼接图形,可以使用电子白板中数学工具的XY原点的功能,方便学生让图形在拼接的过程中从一个顶点出发.
三、再次探究,碰 撞思维 经历再次探究的学习,不仅让学生在平面图形镶嵌的探究中得到升华,更让学生在学习过程中有不怕吃苦的精神,培养学生坚强的意志力. 学生课后经历填写实验报告的过程,体现了数学学习的延续性,并培养学生的归纳能力. 再次探究:限用边长相等的两种正多边形进行平面镶嵌,分别有哪两种正 多边形能行? 教师根据学生 的探究结果最后展 示两种正多边形镶 嵌.如下图: 让学生课后完成再次探究的实验报告. 学生小组交流讨论,并做好记录,并把实验操作的结果让老师用ipad传送到白板上,通过投影展示给大家看. 学生课后完成学案中的实验报告.并对再次探究的问题进行总结. 利用电子白板的注释功能将屏幕显示成桌面的形式,再利用ipad和电脑中安装的软件将学生各小组实验的结果展示给大家看,并加以点评. 利用使用电子白板的隐藏功能将教师的结果展示给大家看. 再次利用电子白板的隐藏功能呈现再次探究的归纳总结.
四、延伸拓展,问 题升华 从特殊到一般,加深 学生对平面图形镶嵌知识的进一步认识,从中体现数学思想. 为学生课后学习数学提升一个高度,数学学习不仅局限于课堂上,更重要的是由一节课给我们带来的启发和思考. 问题:任意的一些形状、大小相同的三角形或四边形能否镶嵌成平面图案? 教师再白板上动手操作任意三角形的镶嵌,并强调就一个顶点的位置要求不同的角拼在一起,其次要求边长相等的要求在一起. 对于任意四边形的镶嵌,教师根据学生在白板上操作的结果给出两种方案: (方案1) (方案2) 教师要指出本节课所指的镶嵌应是方案2,只有这样才能平铺整个平面. 思考:还有其它的任意多边形可以镶嵌成功吗? 教师展示自己博客上的链接,学生记录,方便日后探究思考. 学生思考,脑海中呈现形象,并观看老师对任意三角形镶嵌的过程. 学生在白板上展示 任意四边形镶嵌的结果.(如果过程中有遇到困难,再请其他学生帮忙,共同完成) 学生思考. 学生记下教师的博客地址方便日后交流学习. 利用电子白板中数学工具的XY原点的功能,教师演示任意三角形可以镶嵌成功. 再利用电子白板的填充颜色的功能,将三角形喷出不同的颜色,让学生可以直观的看出任意三角形在拼接的过程中边长相等的应拼接在一起,各个不同的内角应放在一个顶点处. 利用电子白板的隐藏与显示的功能将任意四边形的镶嵌结果展示给大家看.对于学生在动手操作过程中出现的所有现象都要有预设和备份. 在拓展中利用网络链接将教师的博客与学生分享和交流知识.更加提升本节课之后学生的学习态度和探究精神.
五、课堂回顾,课外延 伸 回顾知识,完成作业,使活动得到延续,并引发思考. 1.利用框架引导学生回忆本节课的探究活动,视频展示生活中各种各样 的镶嵌的图片. 2.布置课后作业 (1)完成再次探究中的实验报告. (2)根据所学的镶嵌知识为新年设计画报. (3)思考:三种边长相同的正多边形可以进行镶嵌吗?如果能,有哪些?(选做) 学生跟着教师总结 并反思. 学生完成课后的作业. 利用电子白板的插入视频功能让学生欣赏生活中各种镶嵌的图片,感受数学来源于生活,又服务于生活.
课名 《平面镶嵌》 教师姓名
学科(版本) 人教版数学 章节 上册十一章 数学活动课
学时 第一课时 年级 八年级
一、教学目标 1.知识与技能 (1)通过对平面图形镶嵌问题的探究与解决(当然不一定能完全解决)的过程,加深对正多边形的有关概念、性质的理解; (2)经历实验、探究的学习过程,掌握同一种或两种正多边形镶嵌的问题以及任意三角形或四边形的镶嵌. (3)任意的三角形或四边形的镶嵌. 2.过程与方法 在探究的过程中让学生了解数学知识在实际生产生活中的应用,培养学生应用数学解决实问题的意识和能力; 3.情感态度与价值观 经历探究学习优化学生的思维品质,培养学生发散性思维能力及由特殊到一般的归纳能力;通过合作学习,培养学生团结协作的团队精神.
二、学习者分析 对于八年级学生而言,他们刚刚学习了多边形内角和与正多边形的相关概念,所以学生介于对于多边形的内角度数的了解来学习平面图形的镶嵌.教学的主题是把日常生活中的铺地砖的问题抽象为数学中的平面图形的镶嵌问题. 并利用平面图形镶嵌的知识应用于生活中去. 本节课设计的理论支撑点是建构主义的学习理论,这种理论认为学生的学习不是被动的接受,而是一种主动的探究与建构,认为各个个体对知识的理解随个人的经验、经历的不同而不同. 根据这一理论,教师在教学设计中充分考虑到学生的差异,设计一系列的探究活动是从简单到复杂,从特殊到一般,教学中采用小组合作学习的方式,以学生为主体,让学生自己发现问题、思考问题、解决问题,拓展问题.整个课堂中全体学生都参与进来,学生真正的作为自己学习的主人,教师只是引领者和指导者.
三、教学重难点分析及解决措施 教学重点:1.探究边长相等的同一种正多边形或两种正多边形的镶嵌. 2.任意的三角形或四边形的镶嵌. 教学难点:探究边长相等同一种正多边形或两种正多边形的镶嵌的过程. 解决重难点的措施: 1.通过网络和交互式电子白板的“置顶”功能,展示生活中的各种贴地砖和墙砖的图片,带领学生进入学习情境,激发学生的学习兴趣,通过“感知概念—初次探究—再次探究—延伸拓展”四个层次递进的环节,引导学生对平面图形镶嵌活动的探究. 2.在探究边长相等的一种正多边形的镶嵌环节时,利用交互式电子白板的“拖动副本”、“限制器”和数学工具的功能让学生在白板上动手操作探究,同时其余学生利用学具进行动手操作探究.
四、教学设计
教学环节 环节目标 教学内容 学生活动 媒体作用及分析
一、展示情景,给出概念 结合图片,让学生初步感知从贴地砖的生活现象中蕴含着数学道理,了解从一个顶点处围成360度的角就可以无缝隙,无重叠,从而引出平面图形镶嵌的概念. 1.观察图片,感知表象 展示图片,感知镶嵌. 提出问题:你觉得贴地砖的过程中需要注意什么?蕴含着哪些数学知识? 2.回归数学,给出概念 平面图形的镶嵌:用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称平面图形的镶嵌. 生观察图片,获得感知. 生:图片中的地砖都是铺得平平的,地砖的大小是一样的,顶点在一个点处. 生:这些地砖之间没有一点空隙,也没有重叠在一起. 全体生齐声朗读概念,了解平面图形的镶嵌. 利用电子白板的后置的功能,逐步的显示图片,从而引起学生注意,激发学生的学习兴趣,今儿引入本节课—平面图形的镶嵌. 利用电子白板的书写功能,通过画直线和方框强调概念中的相关语句,加深学生对平面图形镶嵌的理解.
二、初次探究,小试牛 刀 培养学生合作探 究的能力. 学生在活动中了解数学结论的得出不仅仅通过实验,还需要进行推理验证,从而培养学生学习数学的严谨性和思维的缜 密性. 探究:限用同一种正多边形进行平面镶嵌,哪几种正多 边形可以? 教师针对学生拼图结果加以点评,并提问:1.为什 么正三角形、正四边形、正六边形可以镶 嵌? 对于问题1教师举出反例说明,以正五边形为例.如下图: 2.对于一种正多边形的镶嵌为什么只有正三角形、正四边形、正六边形可以成功? 正多边形的每一个内角不可能是,所以对于一种正边形的镶嵌只有正三角形、正四边形、正六边形. 同学们拿出准备好的各种正多边形纸板,在小组内拼 图、记录. 拼接成功的小组派 代表在白板上拼图. 学生独立思考回答问题1.从一个顶点出发围成360度是无缝隙、无重叠的. 学生再次思考教师提出的问题2,并根据教师的引导得出对于一种正多边形的镶嵌只有正三角形、正四边形、 正六边形. 利用电子白板中拖动副本和限制器的功能,可以无限制的使用图形并不改变图形的大小. 学生在白板上进行拼接图形,可以使用电子白板中数学工具的XY原点的功能,方便学生让图形在拼接的过程中从一个顶点出发.
三、再次探究,碰 撞思维 经历再次探究的学习,不仅让学生在平面图形镶嵌的探究中得到升华,更让学生在学习过程中有不怕吃苦的精神,培养学生坚强的意志力. 学生课后经历填写实验报告的过程,体现了数学学习的延续性,并培养学生的归纳能力. 再次探究:限用边长相等的两种正多边形进行平面镶嵌,分别有哪两种正 多边形能行? 教师根据学生 的探究结果最后展 示两种正多边形镶 嵌.如下图: 让学生课后完成再次探究的实验报告. 学生小组交流讨论,并做好记录,并把实验操作的结果让老师用ipad传送到白板上,通过投影展示给大家看. 学生课后完成学案中的实验报告.并对再次探究的问题进行总结. 利用电子白板的注释功能将屏幕显示成桌面的形式,再利用ipad和电脑中安装的软件将学生各小组实验的结果展示给大家看,并加以点评. 利用使用电子白板的隐藏功能将教师的结果展示给大家看. 再次利用电子白板的隐藏功能呈现再次探究的归纳总结.
四、延伸拓展,问 题升华 从特殊到一般,加深 学生对平面图形镶嵌知识的进一步认识,从中体现数学思想. 为学生课后学习数学提升一个高度,数学学习不仅局限于课堂上,更重要的是由一节课给我们带来的启发和思考. 问题:任意的一些形状、大小相同的三角形或四边形能否镶嵌成平面图案? 教师再白板上动手操作任意三角形的镶嵌,并强调就一个顶点的位置要求不同的角拼在一起,其次要求边长相等的要求在一起. 对于任意四边形的镶嵌,教师根据学生在白板上操作的结果给出两种方案: (方案1) (方案2) 教师要指出本节课所指的镶嵌应是方案2,只有这样才能平铺整个平面. 思考:还有其它的任意多边形可以镶嵌成功吗? 教师展示自己博客上的链接,学生记录,方便日后探究思考. 学生思考,脑海中呈现形象,并观看老师对任意三角形镶嵌的过程. 学生在白板上展示 任意四边形镶嵌的结果.(如果过程中有遇到困难,再请其他学生帮忙,共同完成) 学生思考. 学生记下教师的博客地址方便日后交流学习. 利用电子白板中数学工具的XY原点的功能,教师演示任意三角形可以镶嵌成功. 再利用电子白板的填充颜色的功能,将三角形喷出不同的颜色,让学生可以直观的看出任意三角形在拼接的过程中边长相等的应拼接在一起,各个不同的内角应放在一个顶点处. 利用电子白板的隐藏与显示的功能将任意四边形的镶嵌结果展示给大家看.对于学生在动手操作过程中出现的所有现象都要有预设和备份. 在拓展中利用网络链接将教师的博客与学生分享和交流知识.更加提升本节课之后学生的学习态度和探究精神.
五、课堂回顾,课外延 伸 回顾知识,完成作业,使活动得到延续,并引发思考. 1.利用框架引导学生回忆本节课的探究活动,视频展示生活中各种各样 的镶嵌的图片. 2.布置课后作业 (1)完成再次探究中的实验报告. (2)根据所学的镶嵌知识为新年设计画报. (3)思考:三种边长相同的正多边形可以进行镶嵌吗?如果能,有哪些?(选做) 学生跟着教师总结 并反思. 学生完成课后的作业. 利用电子白板的插入视频功能让学生欣赏生活中各种镶嵌的图片,感受数学来源于生活,又服务于生活.
