人教版八年级数学上册12.2 《三角形全等的判定和性质综合应用》教案
文档属性
| 名称 | 人教版八年级数学上册12.2 《三角形全等的判定和性质综合应用》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览

文档简介
三角形全等的判定和性质综合与应用
学习内容: 三角形全等的判定复习
学习目标:
1.进一步掌握三角形全等的条件
2.在解决问题的过程培养学生的分析推理及简单的证明的能力
学习重点(难点):三角形全等的条件的应用
学习方法:讲练结合法
1、 知识要点回顾
1.全等三角形的概念: 的两个三角形叫做全等三角形。
2.全等三角形的性质:全等三角形的对应边 ,对应角 。
3.全等三角形的判定:(1)一般三角形全等的判定: 。
(2)直角三角形全等的判定: 。
注意(1)“分别对应相等”是关键。
(2)两边及其中一边的对角分别对应相等的两个三角形不一定全等。
二、三角形全等判定的思路
1如图1,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌△DCB.
2.如图2,已知∠C=∠D,要判定△ABC≌△ABD,需要添加的一个条件是 。
3.如图3,已知∠1=∠2要要判定△ABC≌△CDA, 需要添加的一个条件是 。
4.如图4,已知∠B=∠E,要判定△ABC≌△AED,需要添加的一个条件是 。
1.已知;如图5,B、C、E三点在同一直线上,AC∥DE,AC=CE, ∠ACD=∠B,
求证:△ABC≌△CDE
2.如图6,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2。
3.已知,如图7,C为BE上一点,点A,D分别在BE两侧,
AB∥ED,AB=CE,BC=ED求证:AC=CD
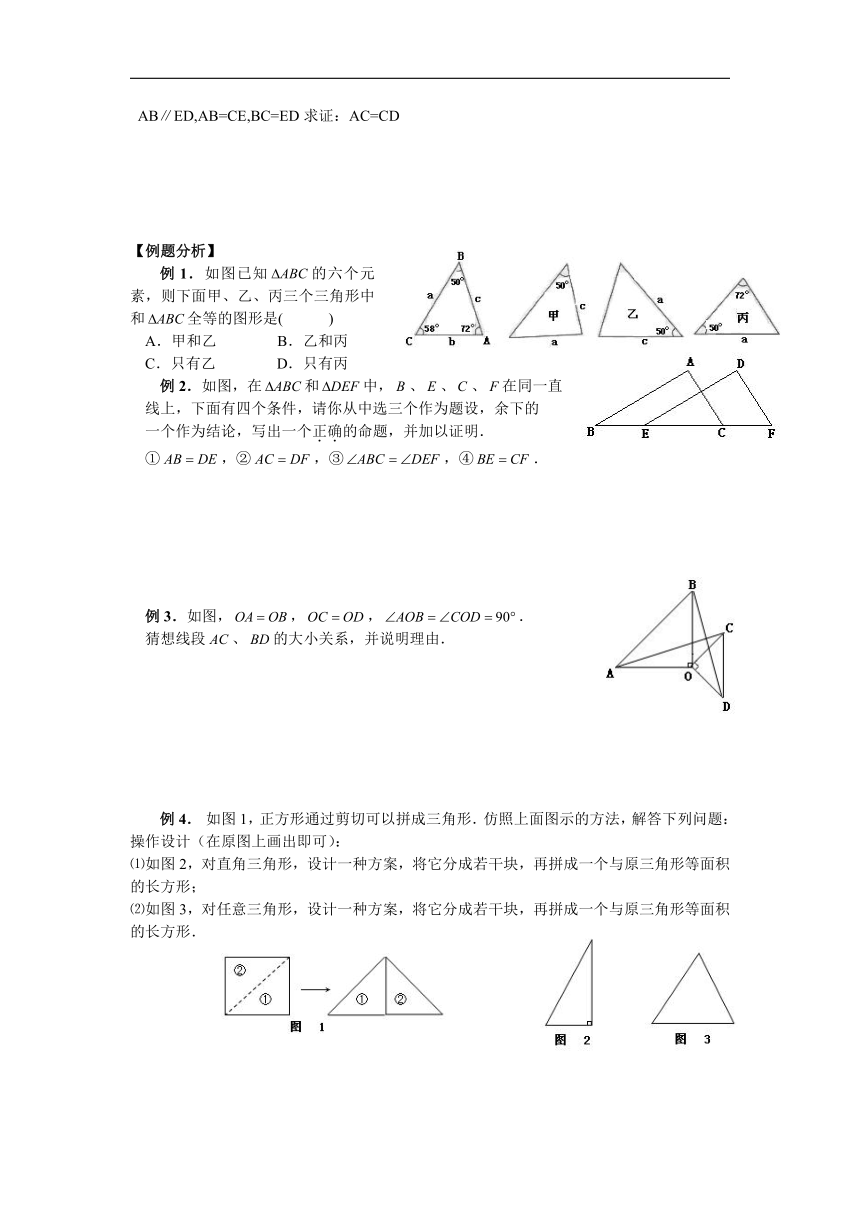
【例题分析】
例1.如图已知的六个元素,则下面甲、乙、丙三个三角形中和全等的图形是( )
A.甲和乙 B.乙和丙
C.只有乙 D.只有丙
例2.如图,在和中,、、、在同一直
线上,下面有四个条件,请你从中选三个作为题设,余下的
一个作为结论,写出一个正确的命题,并加以证明.
①,②,③,④.
例3.如图,,,.
猜想线段、的大小关系,并说明理由.
例4. 如图1,正方形通过剪切可以拼成三角形.仿照上面图示的方法,解答下列问题:操作设计(在原图上画出即可):
⑴如图2,对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的长方形;
⑵如图3,对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的长方形.
【自能训练】
1.下列给出的四组条件中,能判定≌的是( )
A.,, B.,,
C.,, D., , 周长=周长
2.若≌,且的周长为20,,,则长为( )
A.5 B.8 C.7 D.5或8
3.如图,在上,在上,且,那么补充下列一个条件后,仍无法判定≌的是( )
A. B. C. D.
4.如图,将两根钢条、的中点连在一起,使、可以绕着点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
5.在和中,,,,,且,那么这两个三角形( )A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
6.如图,若≌,则等于( )
A.30° B.50° C.60° D.100°
7. 已知,,,请问图中有哪几对全等三角形?并任选其中一对给予证明.
8.如图,给出五个等量关系:①;②;③;④;⑤.请你以其中两个为条件,另三个中的一个为结论,写出一个正确的命题(只需写出一种情况),并加以证明.
9.如图,和都是等边三角形,连接,交于.
求证:⑴; ⑵
三 综合运用,自我检测
1. 下列各组图形是全等形的是( )
A 所有的直角三角形 B斜边和一个锐角相等的两个直角三角形
C 有一个角是50°两个等腰三角形 D两个等边三角形
5. 如图把△ABC绕点A旋转到△ADE,使点D落到BC上,
若∠ADB+∠EDC=110°则∠ABC=___
6.已知如图,AB=AD,AC平分∠DAB,则图中有___对全等
的三角形,它们分别是______
8.已知:D是△ABC的边AB上的一点,AB∥FC,DF角AC与点E,
DE=EF 求证 AE=CE
10.两组邻边分别相等的四边形叫筝形,如图在筝形ABCD中,AB=AD
BC=DC,AC BD相交与点O
求证(1)△ABC≌△ADC
(2)OB=OD AC⊥BD
(1) AC=6 BD=4 求:筝形ABCD的面积
学习内容: 三角形全等的判定复习
学习目标:
1.进一步掌握三角形全等的条件
2.在解决问题的过程培养学生的分析推理及简单的证明的能力
学习重点(难点):三角形全等的条件的应用
学习方法:讲练结合法
1、 知识要点回顾
1.全等三角形的概念: 的两个三角形叫做全等三角形。
2.全等三角形的性质:全等三角形的对应边 ,对应角 。
3.全等三角形的判定:(1)一般三角形全等的判定: 。
(2)直角三角形全等的判定: 。
注意(1)“分别对应相等”是关键。
(2)两边及其中一边的对角分别对应相等的两个三角形不一定全等。
二、三角形全等判定的思路
1如图1,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌△DCB.
2.如图2,已知∠C=∠D,要判定△ABC≌△ABD,需要添加的一个条件是 。
3.如图3,已知∠1=∠2要要判定△ABC≌△CDA, 需要添加的一个条件是 。
4.如图4,已知∠B=∠E,要判定△ABC≌△AED,需要添加的一个条件是 。
1.已知;如图5,B、C、E三点在同一直线上,AC∥DE,AC=CE, ∠ACD=∠B,
求证:△ABC≌△CDE
2.如图6,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2。
3.已知,如图7,C为BE上一点,点A,D分别在BE两侧,
AB∥ED,AB=CE,BC=ED求证:AC=CD
【例题分析】
例1.如图已知的六个元素,则下面甲、乙、丙三个三角形中和全等的图形是( )
A.甲和乙 B.乙和丙
C.只有乙 D.只有丙
例2.如图,在和中,、、、在同一直
线上,下面有四个条件,请你从中选三个作为题设,余下的
一个作为结论,写出一个正确的命题,并加以证明.
①,②,③,④.
例3.如图,,,.
猜想线段、的大小关系,并说明理由.
例4. 如图1,正方形通过剪切可以拼成三角形.仿照上面图示的方法,解答下列问题:操作设计(在原图上画出即可):
⑴如图2,对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的长方形;
⑵如图3,对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的长方形.
【自能训练】
1.下列给出的四组条件中,能判定≌的是( )
A.,, B.,,
C.,, D., , 周长=周长
2.若≌,且的周长为20,,,则长为( )
A.5 B.8 C.7 D.5或8
3.如图,在上,在上,且,那么补充下列一个条件后,仍无法判定≌的是( )
A. B. C. D.
4.如图,将两根钢条、的中点连在一起,使、可以绕着点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
5.在和中,,,,,且,那么这两个三角形( )A.一定不全等 B.一定全等
C.不一定全等 D.以上都不对
6.如图,若≌,则等于( )
A.30° B.50° C.60° D.100°
7. 已知,,,请问图中有哪几对全等三角形?并任选其中一对给予证明.
8.如图,给出五个等量关系:①;②;③;④;⑤.请你以其中两个为条件,另三个中的一个为结论,写出一个正确的命题(只需写出一种情况),并加以证明.
9.如图,和都是等边三角形,连接,交于.
求证:⑴; ⑵
三 综合运用,自我检测
1. 下列各组图形是全等形的是( )
A 所有的直角三角形 B斜边和一个锐角相等的两个直角三角形
C 有一个角是50°两个等腰三角形 D两个等边三角形
5. 如图把△ABC绕点A旋转到△ADE,使点D落到BC上,
若∠ADB+∠EDC=110°则∠ABC=___
6.已知如图,AB=AD,AC平分∠DAB,则图中有___对全等
的三角形,它们分别是______
8.已知:D是△ABC的边AB上的一点,AB∥FC,DF角AC与点E,
DE=EF 求证 AE=CE
10.两组邻边分别相等的四边形叫筝形,如图在筝形ABCD中,AB=AD
BC=DC,AC BD相交与点O
求证(1)△ABC≌△ADC
(2)OB=OD AC⊥BD
(1) AC=6 BD=4 求:筝形ABCD的面积
