余弦定理
图片预览








文档简介
课件26张PPT。余弦定理山西省运城盐化中学 刘俊文一、复习回顾1.正弦定理及其推论: =2R(R为△ABC外接圆半径)BCAabc思考: 在△ABC中,已知AB=2,BC=5,△ABC的面积为4,
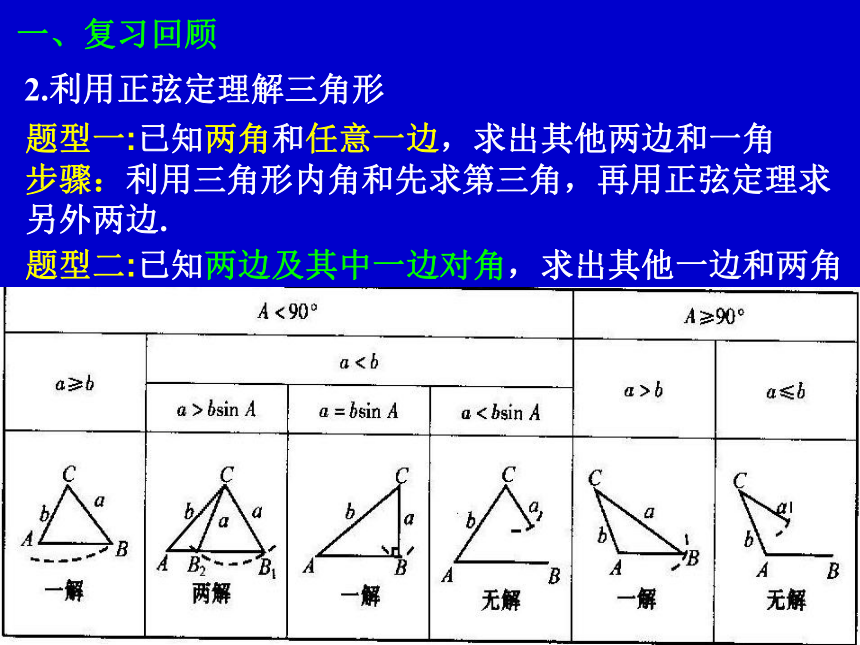
∠ABC=θ,则sinθ= .练习:在△ABC中, ,求此三角形的面积.2.利用正弦定理解三角形题型一:已知两角和任意一边,求出其他两边和一角
步骤:利用三角形内角和先求第三角,再用正弦定理求另外两边.
题型二:已知两边及其中一边对角,求出其他一边和两角一、复习回顾若已知a、b、A的值,则解该三角形的步骤如下:
(1)先利用 求出sinB,从而求出角B;
(2)利用A、B求出角C=180o-(A+B);
(3)再利用 求出边c.注意:求角B时应注意检验!⑵若A为直角或钝角时: a≥b bsinA b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC你能用文字说明吗? 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。归纳变一变乐在其中 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC变形归纳问题1:勾股定理与余弦定理有何关系?勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.问题2:公式的结构特征怎样?(1)轮换对称,简洁优美;剖 析 定 理(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
(3)已知a、b、c(三边),可以求什么?剖 析 定 理(1)已知三边求三个角;问题3:余弦定理在解三角形中的作用是什么?(2)已知两边和它们的夹角,求第三边和其他两个角.剖 析 定 理(3)判断三角形的形状,求三角形的面积例1:在△ABC中,已知b=60cm,c=34cm,A=41o,
解该三角形(角度精确到1°,边长精确到1cm).解:∵a2=b2+c2-2bccosA
=602+342-2×60×34×cos41o≈1676.82
∴a≈41(cm)故由正弦定理可得∵c∴利用计算器可求得 C≈33°
∴B=180o-(A+C) ≈ 180o-(41o+33o)=106°三、例题讲解 一般地,在“知三边及一角”要求剩下的两个角时,应先求最小的边所对的角.例2.在△ABC中,已知a=134.6cm,b=87.8cm,
c=161.7cm,解三角形(角度精确到1′)。解:∴A≈56°20′∴B≈32°53′三、例题讲解例 3、在?ABC中,已知a=7,b=10,
c=6,求A、B和C.解:∴ A≈44°∴ C≈36°∴ B=180°-(A+C)≈100°.例4、已知△ABC中,a=8,b=7,B=600,
求c及S△ABC整理得:c2-8c+15=0解得:c1=3, c2=5例 5 ΔABC三个顶点坐标为A(6,5)、B(-2,8)、C(4,1),求角A.
解法一:
∵ |AB| =
|BC| =
|AC| = ∴ A≈84°.解法二:∵ =(–8,3), =(–2,–4).
∴ cosA= = ,∴ A≈84°.
2.余弦定理3.由余弦定理知1.证明定理:向量法、解析法五、课堂小结(1)已知三边求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.5.余弦定理的作用(3)判断三角形的形状,求三角形的面积4.余弦定理适用于任何三角形解三角形的四种基本类型:1.在△ABC中,b CosA=a cosB,则三角形为( )?
A.直角三角形 B.锐角三角形?C.等腰三角形?D.等边三角形C解法一:利用余弦定理将角化为边.
∵bcosA=acosB?,∴b2+c2-a2=a2+c2-b2?,∴a2=b2?,∴a=b,
故此三角形是等腰三角形. 解法二:利用正弦定理将边转化为角.?∵bcosA=acosB?
又b=2RsinB,a=2RsinA?,∴2RsinBcosA=2RsinAcosB ∴sinAcosB-cosAsinB=0?∴sin(A-B)=0?
∵0<A,B<π,∴-π<A-B<π?,∴A-B=0 即A=B 故此三角形是等腰三角形.? 练习2. 在△ABC中,若a2>b2+c2,则△ABC为 ;若a2=b2+c2,则△ABC为 ;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为 。 3. 在△ABC中,sinA=2cosBsinC,则三角形为 。? 4. 在△ABC中,BC=3,AB=2,且 ,A= 。 直角三角形等腰三角形锐角三角形钝角三角形120° 5. 在△ABC中,已知sinB·sinC=cos2 ,试判断此三角形的类型.解:∵sinB·sinC=cos2 , ∴sinB·sinC=∴2sinB·sinC=1+cos[180°-(B+C)]
将cos(B+C)=cosBcosC-sinBsinC 代入上式得
cosBcosC+sinBsinC=1, ∴cos(B-C)=1?又0<B,C<π,∴-π<B-C<π?∴B-C=0
∴B=C
故此三角形是等腰三角形.布置作业P 10 A组 3、4
B组 1、2
∠ABC=θ,则sinθ= .练习:在△ABC中, ,求此三角形的面积.2.利用正弦定理解三角形题型一:已知两角和任意一边,求出其他两边和一角
步骤:利用三角形内角和先求第三角,再用正弦定理求另外两边.
题型二:已知两边及其中一边对角,求出其他一边和两角一、复习回顾若已知a、b、A的值,则解该三角形的步骤如下:
(1)先利用 求出sinB,从而求出角B;
(2)利用A、B求出角C=180o-(A+B);
(3)再利用 求出边c.注意:求角B时应注意检验!⑵若A为直角或钝角时: a≥b bsinA
c2=a2+b2-2ab·cosC你能用文字说明吗? 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。归纳变一变乐在其中 a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC变形归纳问题1:勾股定理与余弦定理有何关系?勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.问题2:公式的结构特征怎样?(1)轮换对称,简洁优美;剖 析 定 理(2)每个等式中有同一个三角形中的四个元素,知三求一.(方程思想)
(3)已知a、b、c(三边),可以求什么?剖 析 定 理(1)已知三边求三个角;问题3:余弦定理在解三角形中的作用是什么?(2)已知两边和它们的夹角,求第三边和其他两个角.剖 析 定 理(3)判断三角形的形状,求三角形的面积例1:在△ABC中,已知b=60cm,c=34cm,A=41o,
解该三角形(角度精确到1°,边长精确到1cm).解:∵a2=b2+c2-2bccosA
=602+342-2×60×34×cos41o≈1676.82
∴a≈41(cm)故由正弦定理可得∵c
∴B=180o-(A+C) ≈ 180o-(41o+33o)=106°三、例题讲解 一般地,在“知三边及一角”要求剩下的两个角时,应先求最小的边所对的角.例2.在△ABC中,已知a=134.6cm,b=87.8cm,
c=161.7cm,解三角形(角度精确到1′)。解:∴A≈56°20′∴B≈32°53′三、例题讲解例 3、在?ABC中,已知a=7,b=10,
c=6,求A、B和C.解:∴ A≈44°∴ C≈36°∴ B=180°-(A+C)≈100°.例4、已知△ABC中,a=8,b=7,B=600,
求c及S△ABC整理得:c2-8c+15=0解得:c1=3, c2=5例 5 ΔABC三个顶点坐标为A(6,5)、B(-2,8)、C(4,1),求角A.
解法一:
∵ |AB| =
|BC| =
|AC| = ∴ A≈84°.解法二:∵ =(–8,3), =(–2,–4).
∴ cosA= = ,∴ A≈84°.
2.余弦定理3.由余弦定理知1.证明定理:向量法、解析法五、课堂小结(1)已知三边求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.5.余弦定理的作用(3)判断三角形的形状,求三角形的面积4.余弦定理适用于任何三角形解三角形的四种基本类型:1.在△ABC中,b CosA=a cosB,则三角形为( )?
A.直角三角形 B.锐角三角形?C.等腰三角形?D.等边三角形C解法一:利用余弦定理将角化为边.
∵bcosA=acosB?,∴b2+c2-a2=a2+c2-b2?,∴a2=b2?,∴a=b,
故此三角形是等腰三角形. 解法二:利用正弦定理将边转化为角.?∵bcosA=acosB?
又b=2RsinB,a=2RsinA?,∴2RsinBcosA=2RsinAcosB ∴sinAcosB-cosAsinB=0?∴sin(A-B)=0?
∵0<A,B<π,∴-π<A-B<π?,∴A-B=0 即A=B 故此三角形是等腰三角形.? 练习2. 在△ABC中,若a2>b2+c2,则△ABC为 ;若a2=b2+c2,则△ABC为 ;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为 。 3. 在△ABC中,sinA=2cosBsinC,则三角形为 。? 4. 在△ABC中,BC=3,AB=2,且 ,A= 。 直角三角形等腰三角形锐角三角形钝角三角形120° 5. 在△ABC中,已知sinB·sinC=cos2 ,试判断此三角形的类型.解:∵sinB·sinC=cos2 , ∴sinB·sinC=∴2sinB·sinC=1+cos[180°-(B+C)]
将cos(B+C)=cosBcosC-sinBsinC 代入上式得
cosBcosC+sinBsinC=1, ∴cos(B-C)=1?又0<B,C<π,∴-π<B-C<π?∴B-C=0
∴B=C
故此三角形是等腰三角形.布置作业P 10 A组 3、4
B组 1、2
