1.4.2正弦函数、余弦函数的性质(二)
文档属性
| 名称 | 1.4.2正弦函数、余弦函数的性质(二) |
|
|
| 格式 | zip | ||
| 文件大小 | 162.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-26 00:00:00 | ||
图片预览






文档简介
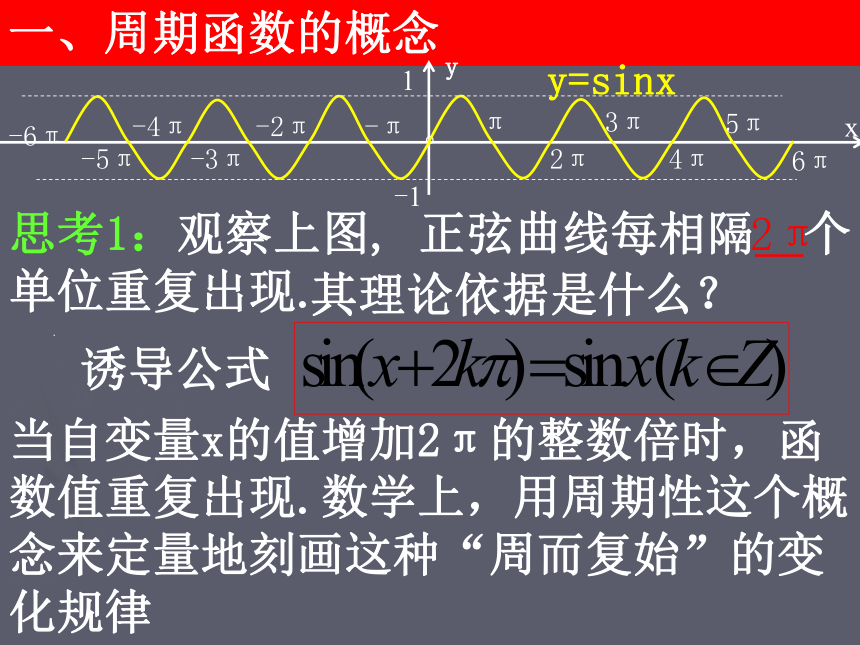
课件19张PPT。1.4.2 正弦函数、余弦函数的性质(二) 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作------周期性一、周期函数的概念 思考1:观察上图, 正弦曲线每相隔 个单位重复出现..2π诱导公式其理论依据是什么?当自变量x的值增加2π的整数倍时,函数值重复出现.数学上,用周期性这个概念来定量地刻画这种“周而复始”的变化规律思考2:设f(x)=sinx,则
可以怎样表示? f(x+2kπ)=f(x) 这就是说:当自变量x的值增加到x+2kπ时,函数值重复出现.
为了突出函数的这个特性,我们把函数f(x)=sinx称为周期函数,2kπ为这个函数的周期 (其中k∈z且k≠0).思考3:把函数f(x)=sinx称为周期函数.那么,一般地,如何定义周期函数呢?【周期函数的定义】对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x)
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期. 思考4:周期函数的周期是否唯一?正弦函数y=sinx的周期有哪些? 答:周期函数的周期不止一个. ±2π,±4π,±6π,…都是正弦函数的周期,事实上,任何一个常数2kπ(k∈z且k≠0)都是它的周期.【周期函数的定义】对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x)
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期. 【最小正周期】 如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期.今后本书中所涉及到的周期,如果不加特别说明,一般都是指函数的最小正周期.【周期函数的定义】对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x)
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期.
【最小正周期】如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期. 答:正弦函数y=sinx有最小正周期,且最小正周期T=2π思考5:我们知道 ±2π,±4π,±6π,…都是y=sinx的周期,那么函数y=sinx有最小正周期吗?若有,那么最小正周期T等于多少? 正弦函数y=sinx是周期函数,2kπ(k∈Z且 k≠0)都是它的周期,最小正周期 T=2π.
余弦函数y=cosx是周期函数,2kπ(k∈Z且 k≠0)都是周期,最小正周期 T=2π.思考6:就周期性而言,对正弦函数有什么结论?对余弦函数呢?二:周期概念的拓展 思考1:判断下列说法是否正确思考2:周期函数的定义域有什么特点? ①函数f(x)=sinx(x≥0)是周期函数( )
②函数f(x)=sinx(x<0)是周期函数( )
③函数f(x)=sinx(x≠3kπ)是周期函数( )
④函数f(x)=sinx,x∈[0,10π]是周期函数( )╳╳╳╳答案:周期函数的定义域是全体实数。 判断下面各题的正误2.y=|sinx|的周期是π且是偶函数.( )3.存在角x使得2cosx=3成立.( )√×× 对,因为|sin(x+π)|=|-sinx|=|sinx|.错,因为余弦函数的最大值为1.随堂练习例1 求下列函数的周期:
⑴y=3cosx,x∈R;
⑵y=sin2x,x∈R;
⑶y=2sin( - ),x∈R; ∵ 3cos(x+2π)=
∴由周期函数的定义可知,原函数的周期为2π【解】⑴3cosx三、例题讲解⑵y=sin2x,x∈R; ∵sin2(x+π)=
∴由周期函数的定义可知,原函数的周期为π
sin2x解:⑶y=2sin( - ),x∈R; ∴由周期函数的定义可知,原函数的周期为4π解:函数y=Asin(ωx+ψ) 从前面的例子可以看出,函数y=Asin(ωx+ψ),x∈R及函数y=Acos(ωx+ψ),x∈R(其中A,ω,ψ为常数,且A≠0,ω>0)的周期仅与自变量的系数有关.那么,如何用自变量的系数表示上述函数的周期呢?及函数y=Acos(ωx+ψ)的周期 事实上,令z=ωx+ψ,那么x∈R必须并且只需z∈R,且函数y=Asinz,z∈R及函数y=Acosz,z∈R的周期都是2π.由于成立的最小正数.从而,函数Asin[ω(x+T)+ψ]= Asin(ωx+ψ),Acos[ω(x+T)+ψ]= Acos(ωx+ψ)y=Asin(ωx+ψ),x∈R及函数y=Acos(ωx+ψ),x∈R 例2 已知定义在R上的函数f(x)满足
f(x+2)+f(x)=0,试判断f(x)是否为周期函数?〖分析〗由已知有:f(x+2)= -f(x)
∴f(x+4)=
即 f(x+4)=f(x)
∴由周期函数的定义知,f(x)是周期函数.f(x)=-[-f(x)]=-f(x+2)f[(x+2)+2]= 如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期 对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x)那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期. 归 纳 整 理 1.说说周期函数的定义.3.什么叫周期函数的最小正周期? 2.函数的周期性是函数的一个基本性质,判断一个函数是否为周期函数,一般以定义为依据,检验它是否存在非零常数T,对定义域内任一实数x,f(x+T)=f(x)恒成立. 4.函数y=Asin(ωx+φ)和y=Acos(ωx+φ) (A>0)的最小
正周期 T=这个公式,解题时可以直接应用练习:P361,2.P463.
高中数学老师欧阳文丰制作------周期性一、周期函数的概念 思考1:观察上图, 正弦曲线每相隔 个单位重复出现..2π诱导公式其理论依据是什么?当自变量x的值增加2π的整数倍时,函数值重复出现.数学上,用周期性这个概念来定量地刻画这种“周而复始”的变化规律思考2:设f(x)=sinx,则
可以怎样表示? f(x+2kπ)=f(x) 这就是说:当自变量x的值增加到x+2kπ时,函数值重复出现.
为了突出函数的这个特性,我们把函数f(x)=sinx称为周期函数,2kπ为这个函数的周期 (其中k∈z且k≠0).思考3:把函数f(x)=sinx称为周期函数.那么,一般地,如何定义周期函数呢?【周期函数的定义】对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x)
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期. 思考4:周期函数的周期是否唯一?正弦函数y=sinx的周期有哪些? 答:周期函数的周期不止一个. ±2π,±4π,±6π,…都是正弦函数的周期,事实上,任何一个常数2kπ(k∈z且k≠0)都是它的周期.【周期函数的定义】对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x)
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期. 【最小正周期】 如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期.今后本书中所涉及到的周期,如果不加特别说明,一般都是指函数的最小正周期.【周期函数的定义】对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有
f(x+T)=f(x)
那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期.
【最小正周期】如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期. 答:正弦函数y=sinx有最小正周期,且最小正周期T=2π思考5:我们知道 ±2π,±4π,±6π,…都是y=sinx的周期,那么函数y=sinx有最小正周期吗?若有,那么最小正周期T等于多少? 正弦函数y=sinx是周期函数,2kπ(k∈Z且 k≠0)都是它的周期,最小正周期 T=2π.
余弦函数y=cosx是周期函数,2kπ(k∈Z且 k≠0)都是周期,最小正周期 T=2π.思考6:就周期性而言,对正弦函数有什么结论?对余弦函数呢?二:周期概念的拓展 思考1:判断下列说法是否正确思考2:周期函数的定义域有什么特点? ①函数f(x)=sinx(x≥0)是周期函数( )
②函数f(x)=sinx(x<0)是周期函数( )
③函数f(x)=sinx(x≠3kπ)是周期函数( )
④函数f(x)=sinx,x∈[0,10π]是周期函数( )╳╳╳╳答案:周期函数的定义域是全体实数。 判断下面各题的正误2.y=|sinx|的周期是π且是偶函数.( )3.存在角x使得2cosx=3成立.( )√×× 对,因为|sin(x+π)|=|-sinx|=|sinx|.错,因为余弦函数的最大值为1.随堂练习例1 求下列函数的周期:
⑴y=3cosx,x∈R;
⑵y=sin2x,x∈R;
⑶y=2sin( - ),x∈R; ∵ 3cos(x+2π)=
∴由周期函数的定义可知,原函数的周期为2π【解】⑴3cosx三、例题讲解⑵y=sin2x,x∈R; ∵sin2(x+π)=
∴由周期函数的定义可知,原函数的周期为π
sin2x解:⑶y=2sin( - ),x∈R; ∴由周期函数的定义可知,原函数的周期为4π解:函数y=Asin(ωx+ψ) 从前面的例子可以看出,函数y=Asin(ωx+ψ),x∈R及函数y=Acos(ωx+ψ),x∈R(其中A,ω,ψ为常数,且A≠0,ω>0)的周期仅与自变量的系数有关.那么,如何用自变量的系数表示上述函数的周期呢?及函数y=Acos(ωx+ψ)的周期 事实上,令z=ωx+ψ,那么x∈R必须并且只需z∈R,且函数y=Asinz,z∈R及函数y=Acosz,z∈R的周期都是2π.由于成立的最小正数.从而,函数Asin[ω(x+T)+ψ]= Asin(ωx+ψ),Acos[ω(x+T)+ψ]= Acos(ωx+ψ)y=Asin(ωx+ψ),x∈R及函数y=Acos(ωx+ψ),x∈R 例2 已知定义在R上的函数f(x)满足
f(x+2)+f(x)=0,试判断f(x)是否为周期函数?〖分析〗由已知有:f(x+2)= -f(x)
∴f(x+4)=
即 f(x+4)=f(x)
∴由周期函数的定义知,f(x)是周期函数.f(x)=-[-f(x)]=-f(x+2)f[(x+2)+2]= 如果在周期函数f(x)的所有周期中存在一个最小的正数, 则这个最小正数叫做f(x)的最小正周期 对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x)那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期. 归 纳 整 理 1.说说周期函数的定义.3.什么叫周期函数的最小正周期? 2.函数的周期性是函数的一个基本性质,判断一个函数是否为周期函数,一般以定义为依据,检验它是否存在非零常数T,对定义域内任一实数x,f(x+T)=f(x)恒成立. 4.函数y=Asin(ωx+φ)和y=Acos(ωx+φ) (A>0)的最小
正周期 T=这个公式,解题时可以直接应用练习:P361,2.P463.
