沪科版数学八年级下册 19.1多边形内角和 课件(共23张)
文档属性
| 名称 | 沪科版数学八年级下册 19.1多边形内角和 课件(共23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 352.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 16:22:47 | ||
图片预览

文档简介
(共23张PPT)
多边形内角和
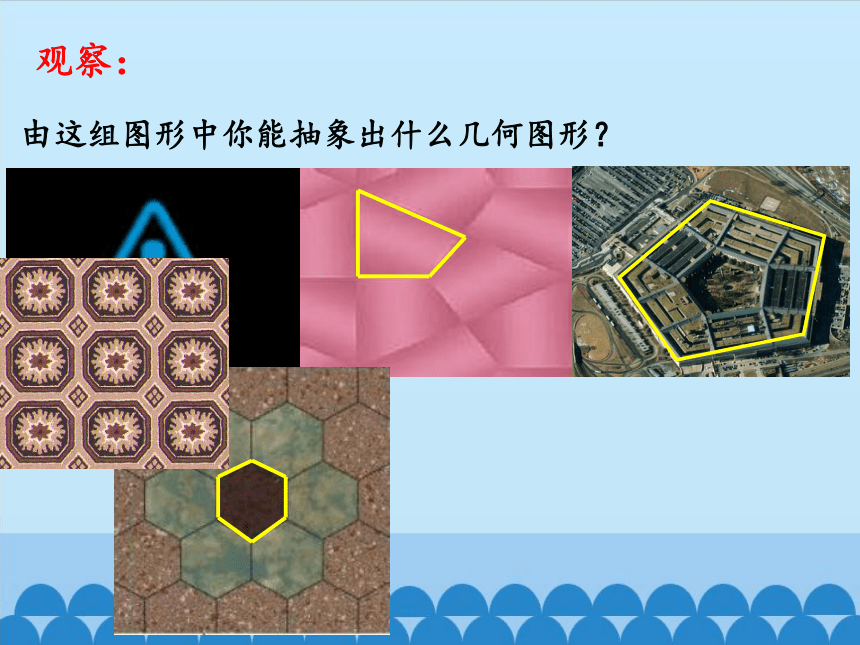
观察:
由这组图形中你能抽象出什么几何图形?
三角形
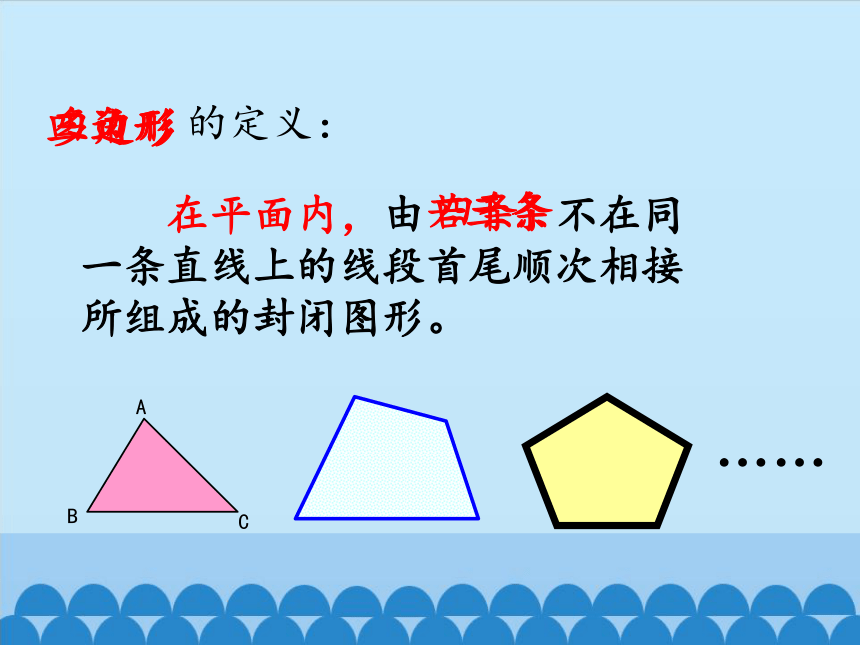
在平面内,由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形。
的定义:
三条
A
B
C
……
若干条
多边形
四边形
四条
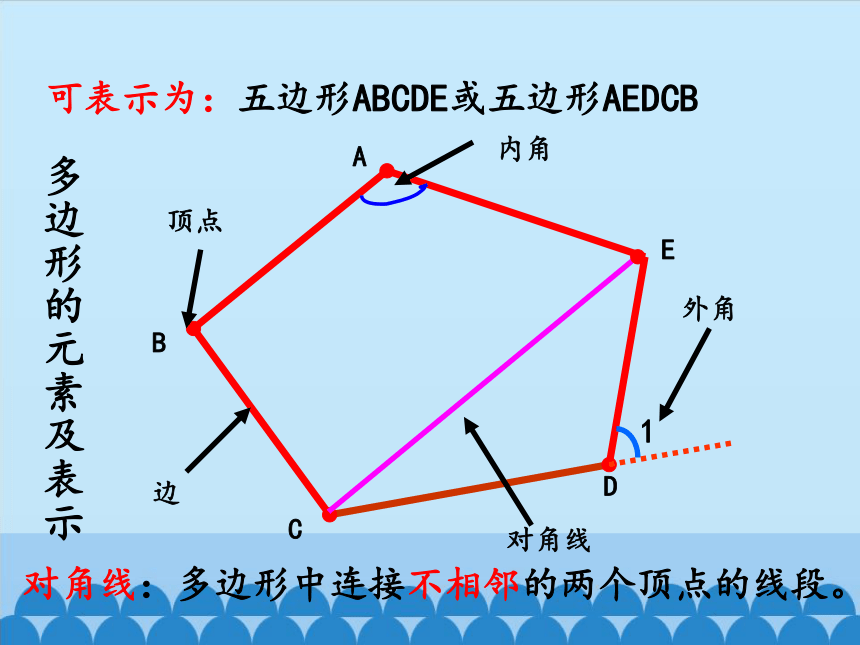
内角
对角线
对角线:多边形中连接不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
多边形的元素及表示
顶点
边
比
一
比
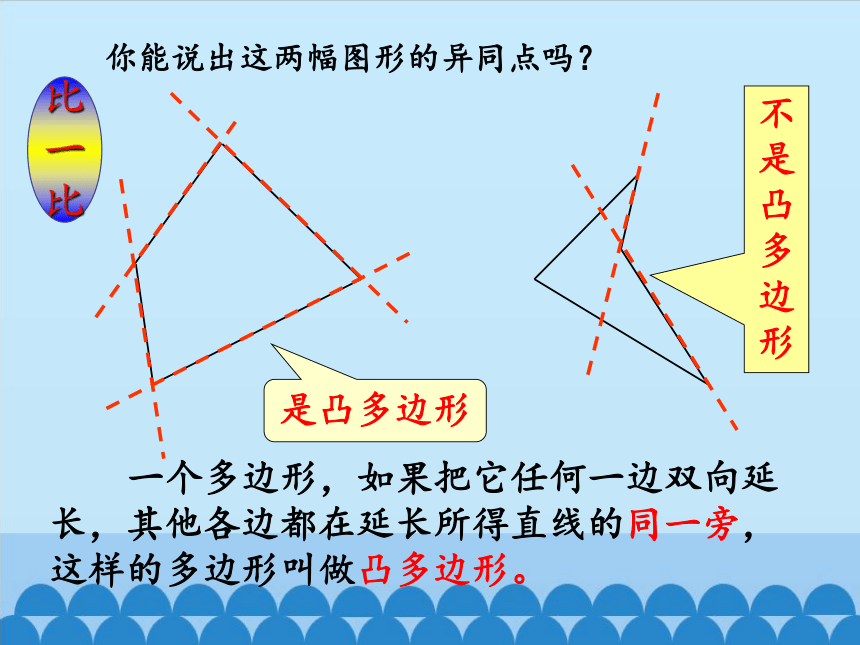
你能说出这两幅图形的异同点吗?
是凸多边形
不是凸多边形
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形。
(1)三角形内角和是多少度?
动手操作,探索新知:
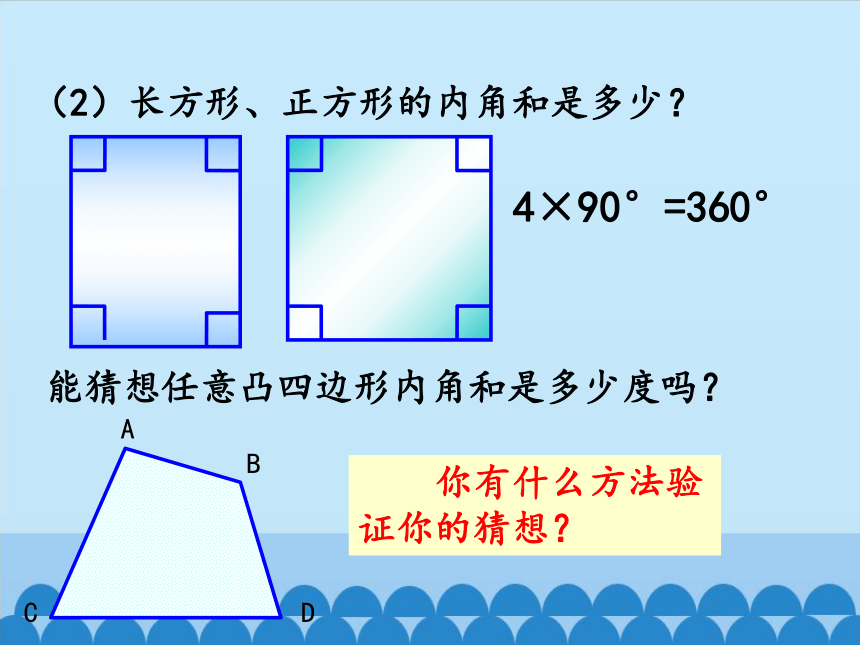
(2)长方形、正方形的内角和是多少?
4×90°=360°
能猜想任意凸四边形内角和是多少度吗?
A
B
C
D
你有什么方法验证你的猜想?
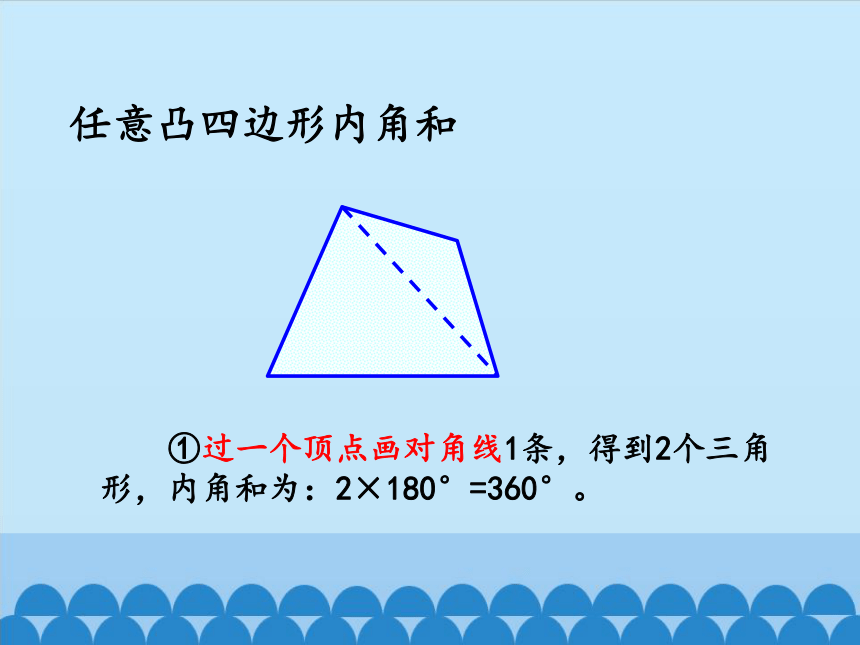
任意凸四边形内角和
①过一个顶点画对角线1条,得到2个三角形,内角和为:2×180°=360°。
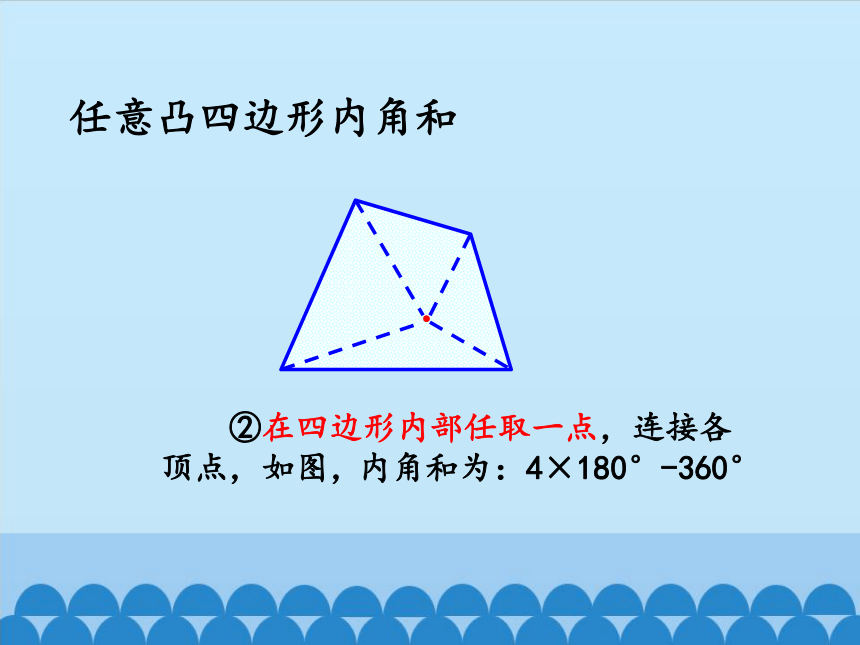
任意凸四边形内角和
②在四边形内部任取一点,连接各顶点,如图,
内角和为:4×180°-360°
任意凸四边形内角和
③在四边形一边上任取一点,连接不相临的各顶点,内角和为:3×180°-180°
任意凸四边形内角和
④在四边形外部任取一点,连接各顶点,如图,
内角和为:3×180°-180°
A
B
C
D
E
想一想:
五边形的内角和是多少度呢?
3×180°=540°
你能动手做一做吗?
按照第一种分割的做法来看:
归纳总结
多边形边数 从一个顶点引出对角线条数 图形 分割成的三角形个数
多边形的内角和
4
5
6
... …… …… …… ……
n
2
2×180°
3
3×180°
4
4×180°
n-2
(n-2)×180°
1
2
3
n-3
定理:n边形的内角和等于
(n-2) 180°
(n为不小于3的整数)
你能证明这个结论吗?
证明:在n边形内部任取一点O,再把点O与各顶点连接,将原多边形分割成n个三角形,n个三角形的内角和减去一个周角,即得n边形的内角和为
180°·n-360°=(n-2)·180°
n边形内角和定理的证明
当堂训练,巩固基础:
1.十边形的内角和为______。
2.已知多边形内角和等于2520°,则它的边数为______。
1440°
16
3.已知多边形每个内角都等于150°,求它的边数及内角和。
解:设此多边形边数为n,由多边形的内角和公式可得:
(n-2)·180°=150°·n
n =12
150°×12 = 1800°
答:此多边形边数为12,内角和为1800°。
练练你的“本领”:
有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
M
N
课堂小结:
(1)通过本节课的学习,你学到了哪些知识和方法?
(2)你认为这节课中最大的收获是什么?
(3)你还有哪些疑惑或不足?
1.我们了解了多边形的相关概念,重点探索了多边形内角和定理。
2.通过探索多边形内角和公式,我们尝试了从不同的角度寻求解决问题的方法,会用多边形的内角和公式进行相关计算。
3.在探索多边形内角和公式时,我们将多边形问题转化为三角形问题,这是数学中解决问题的重要思想方法之一——化归思想,它能将未知的问题转化为已知的问题,复杂的问题转化为简单的问题。
课堂小结:
作业:
做课后练习。
谢 谢
多边形内角和
观察:
由这组图形中你能抽象出什么几何图形?
三角形
在平面内,由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形。
的定义:
三条
A
B
C
……
若干条
多边形
四边形
四条
内角
对角线
对角线:多边形中连接不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
多边形的元素及表示
顶点
边
比
一
比
你能说出这两幅图形的异同点吗?
是凸多边形
不是凸多边形
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形。
(1)三角形内角和是多少度?
动手操作,探索新知:
(2)长方形、正方形的内角和是多少?
4×90°=360°
能猜想任意凸四边形内角和是多少度吗?
A
B
C
D
你有什么方法验证你的猜想?
任意凸四边形内角和
①过一个顶点画对角线1条,得到2个三角形,内角和为:2×180°=360°。
任意凸四边形内角和
②在四边形内部任取一点,连接各顶点,如图,
内角和为:4×180°-360°
任意凸四边形内角和
③在四边形一边上任取一点,连接不相临的各顶点,内角和为:3×180°-180°
任意凸四边形内角和
④在四边形外部任取一点,连接各顶点,如图,
内角和为:3×180°-180°
A
B
C
D
E
想一想:
五边形的内角和是多少度呢?
3×180°=540°
你能动手做一做吗?
按照第一种分割的做法来看:
归纳总结
多边形边数 从一个顶点引出对角线条数 图形 分割成的三角形个数
多边形的内角和
4
5
6
... …… …… …… ……
n
2
2×180°
3
3×180°
4
4×180°
n-2
(n-2)×180°
1
2
3
n-3
定理:n边形的内角和等于
(n-2) 180°
(n为不小于3的整数)
你能证明这个结论吗?
证明:在n边形内部任取一点O,再把点O与各顶点连接,将原多边形分割成n个三角形,n个三角形的内角和减去一个周角,即得n边形的内角和为
180°·n-360°=(n-2)·180°
n边形内角和定理的证明
当堂训练,巩固基础:
1.十边形的内角和为______。
2.已知多边形内角和等于2520°,则它的边数为______。
1440°
16
3.已知多边形每个内角都等于150°,求它的边数及内角和。
解:设此多边形边数为n,由多边形的内角和公式可得:
(n-2)·180°=150°·n
n =12
150°×12 = 1800°
答:此多边形边数为12,内角和为1800°。
练练你的“本领”:
有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
M
N
课堂小结:
(1)通过本节课的学习,你学到了哪些知识和方法?
(2)你认为这节课中最大的收获是什么?
(3)你还有哪些疑惑或不足?
1.我们了解了多边形的相关概念,重点探索了多边形内角和定理。
2.通过探索多边形内角和公式,我们尝试了从不同的角度寻求解决问题的方法,会用多边形的内角和公式进行相关计算。
3.在探索多边形内角和公式时,我们将多边形问题转化为三角形问题,这是数学中解决问题的重要思想方法之一——化归思想,它能将未知的问题转化为已知的问题,复杂的问题转化为简单的问题。
课堂小结:
作业:
做课后练习。
谢 谢
