沪科版数学八年级下册 19.1 多边形内角和 课件(共21张)
文档属性
| 名称 | 沪科版数学八年级下册 19.1 多边形内角和 课件(共21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 312.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览

文档简介
(共21张PPT)
19.1 多边形内角和
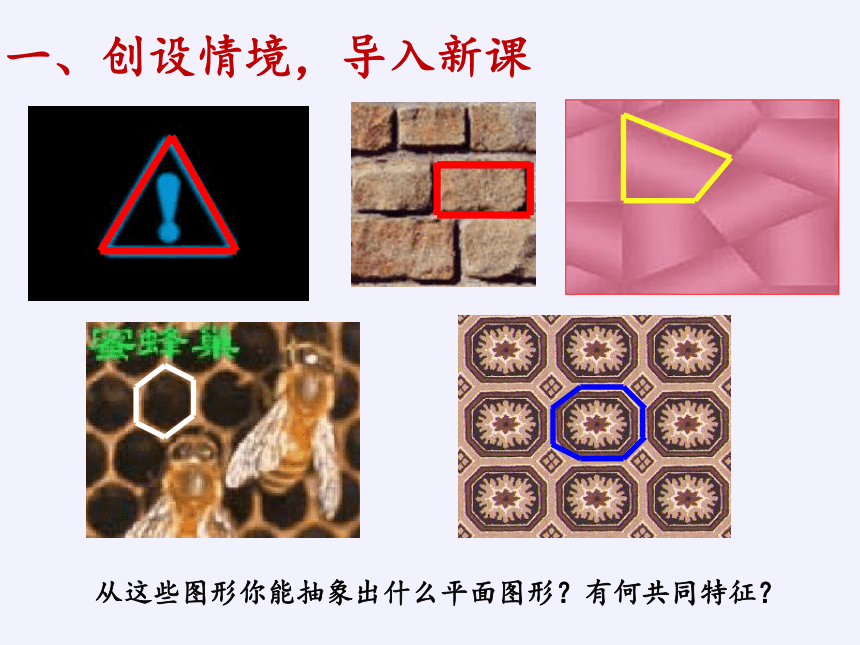
从这些图形你能抽象出什么平面图形?有何共同特征?
一、创设情境,导入新课
三角形
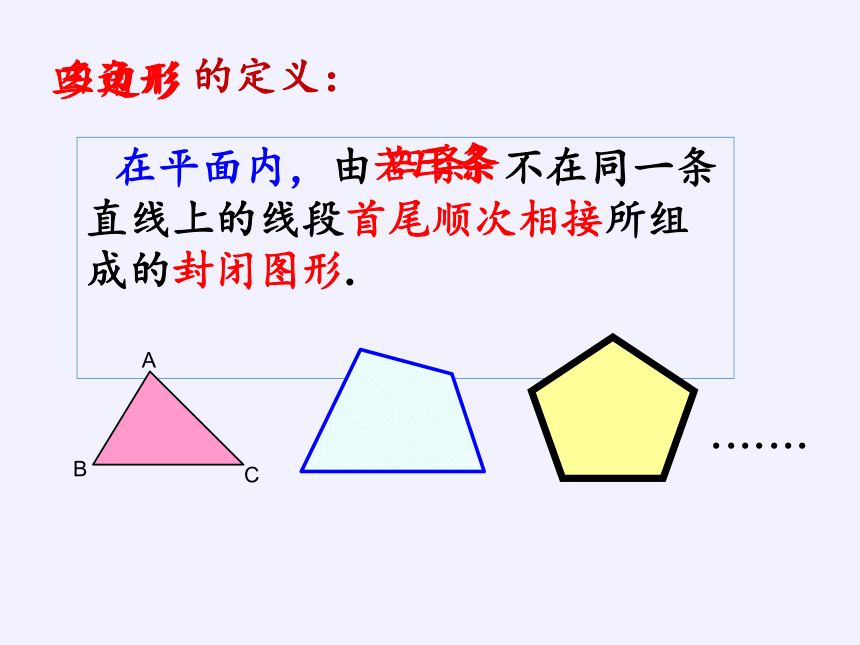
在平面内,由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形.
的定义:
三条
A
B
C
.......
若干条
多边形
四边形
四条
顶点
内角
边
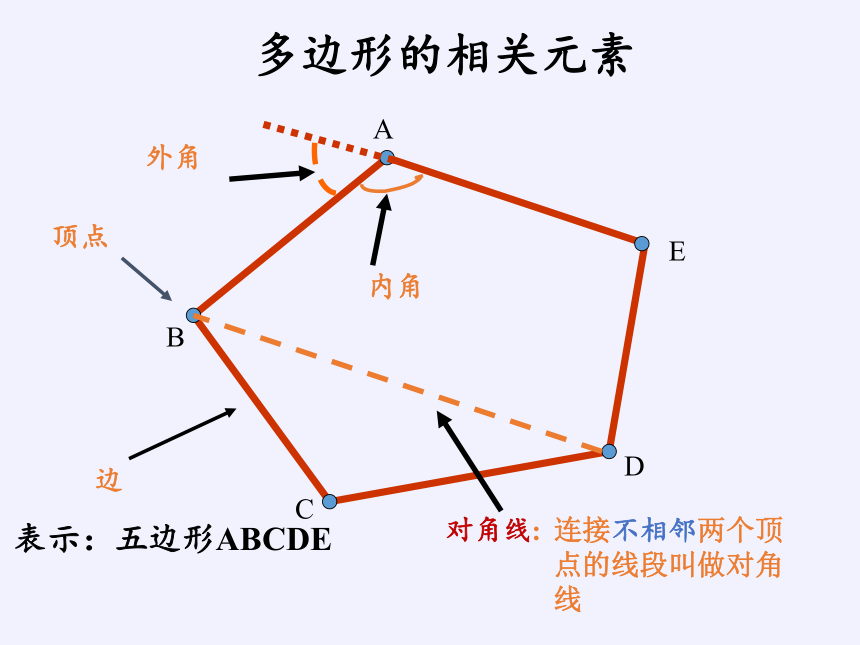
对角线:
多边形的相关元素
外角
表示:五边形ABCDE
A
C
B
D
E
连接不相邻两个顶点的线段叫做对角线
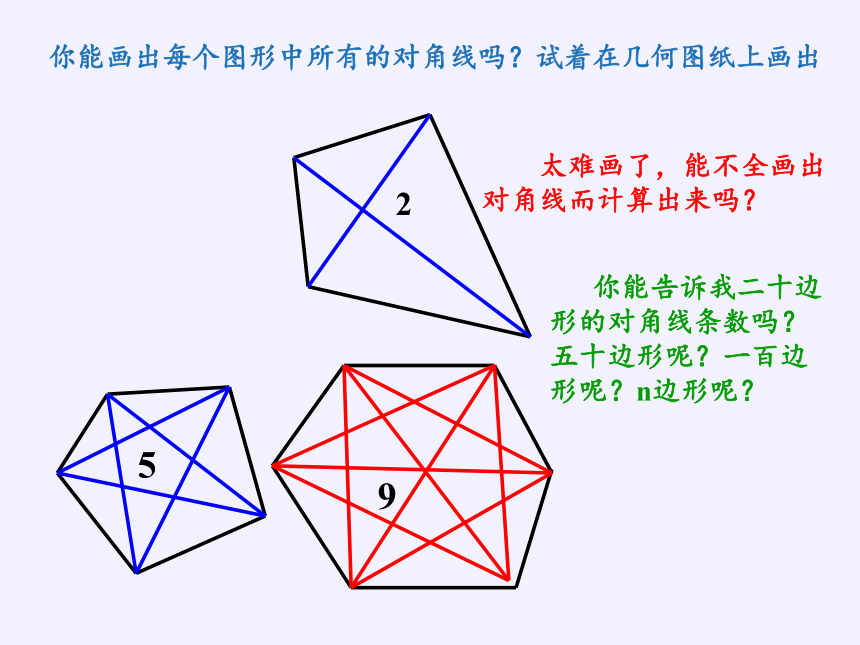
你能画出每个图形中所有的对角线吗?试着在几何图纸上画出
2
5
9
太难画了,能不全画出对角线而计算出来吗?
你能告诉我二十边形的对角线条数吗?五十边形呢?一百边形呢?n边形呢?
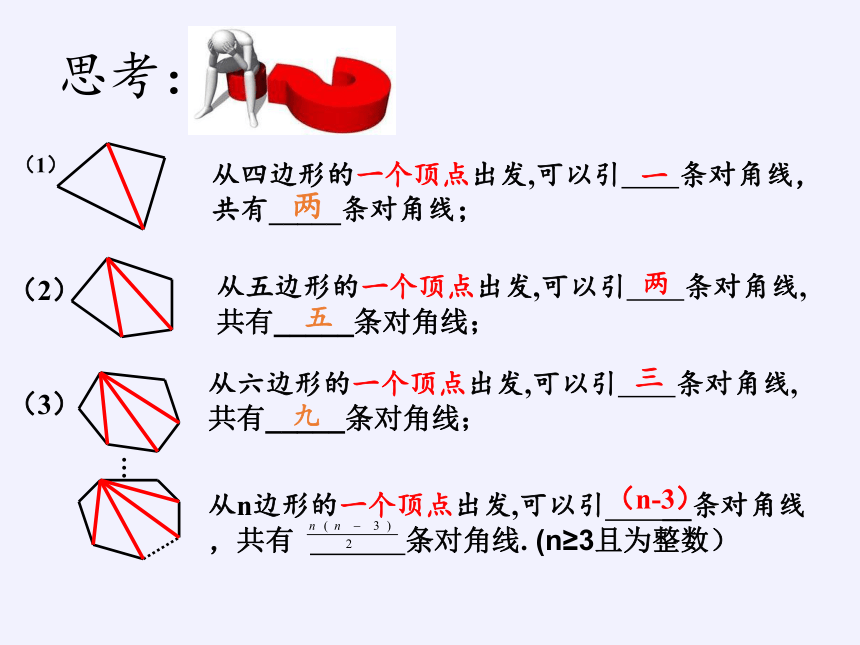
从四边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从五边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从六边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
一
两
三
从n边形的一个顶点出发,可以引 __条对角线,共有 条对角线. (n≥3且为整数)
(n-3)
(1)
(2)
(3)
…
两
五
九
思考:
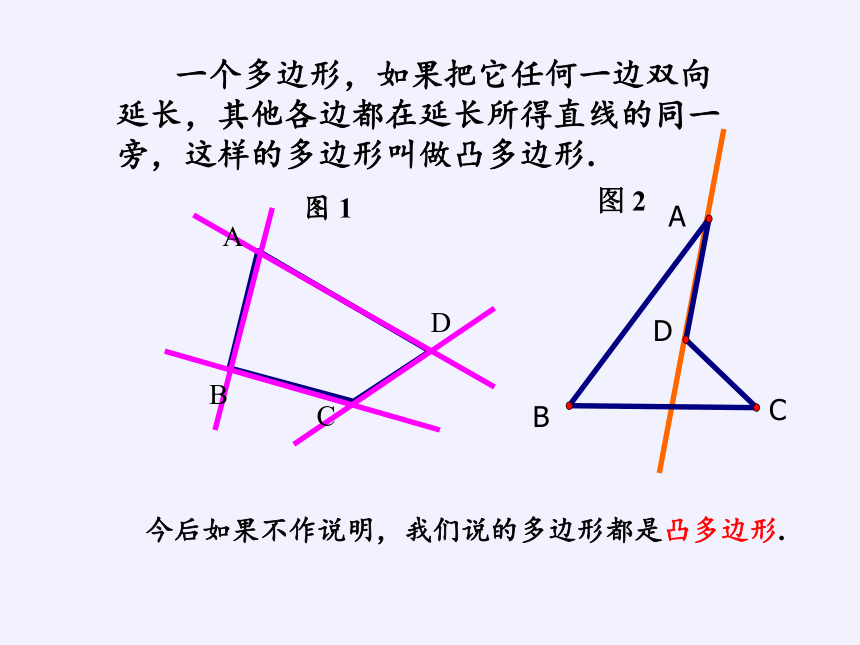
今后如果不作说明,我们说的多边形都是凸多边形.
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
图 1
A
C
B
D
图 2
A
C
B
D
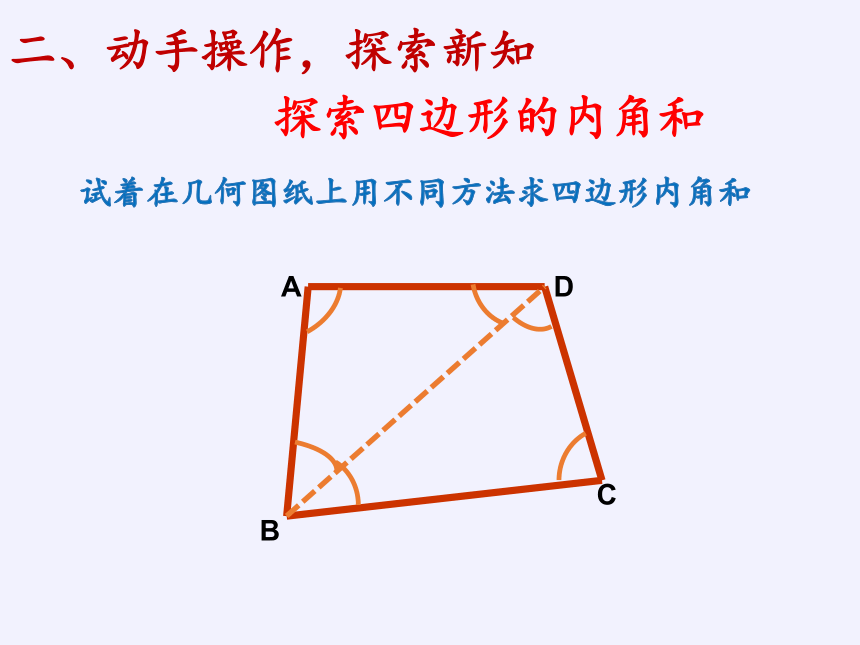
探索四边形的内角和
A
D
C
B
二、动手操作,探索新知
试着在几何图纸上用不同方法求四边形内角和
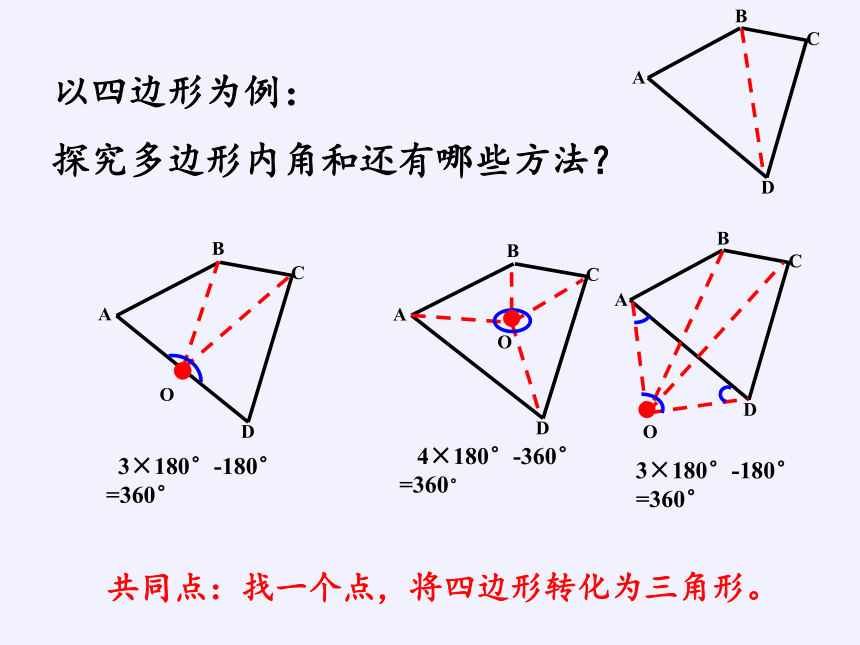
以四边形为例:
探究多边形内角和还有哪些方法?
D
C
B
A
O
D
C
B
A
O
D
C
B
A
O
●
●
●
3×180°-180°
=360°
4×180°-360°
=360°
3×180°-180°
=360°
共同点:找一个点,将四边形转化为三角形。
D
C
B
A
探索五边形的内角和
A
B
C
D
E
类比四边形求内角和,试着在几何图纸上用不同方法求五边形内角和
E
A
B
C
D
.
O
180°×5 - 360° = 540°
A
B
C
D
E
F
180°×4 -180° =540°
共同点:找一个点,将五边形转化为三角形。
探索六边形的内角和
A
B
C
D
E
F
小组讨论探究:选取最佳方法求六边形内角和
180°×4=720°
归纳总结
多边形边数 从一个顶点引出对角线条数 图形 分割成的三角形个数
多边形的内角和
4
5
6
... …… …… …… ……
n
2
2×1800
3
3×1800
4
4×1800
n-2
(n-2)×1800
1
2
3
n-3
探索n边形的内角和
①n代表什么?
② n-2表示什么含义?
③为什么要乘以180°
定理:n边形内角和公式为:______________________________。
(n-2)·180°(n≥3且为整数)
例:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
三、初步应用,感悟新知
变式练习1:已知一个多边形的内角和是2160°,
求它的边数。
解 : 设这个多边形有n条边.由多边形内角和定理知:
即这个多边形有14条边.
(n-2) ×180°=2160°
得 n =14
四、巩固练习
变式练习2:有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
M
N
解:
①三角形,内角和为180°
②四边形,内角和为360°
③五边形,内角和为540°
多边形
分割成三角形
多边形的内角和
转化
归纳
(n-2) · 180°(n ≥3且为整数)
1.多边形有关概念(边、顶点、内角、外角、对角线)
2.
五、课堂小结
3、数学问题的思想方法:如将多边形问题转化为三角形问题,以及类比法、归纳法、分类的思想方法。
谢 谢
19.1 多边形内角和
从这些图形你能抽象出什么平面图形?有何共同特征?
一、创设情境,导入新课
三角形
在平面内,由 不在同一条直线上的线段首尾顺次相接所组成的封闭图形.
的定义:
三条
A
B
C
.......
若干条
多边形
四边形
四条
顶点
内角
边
对角线:
多边形的相关元素
外角
表示:五边形ABCDE
A
C
B
D
E
连接不相邻两个顶点的线段叫做对角线
你能画出每个图形中所有的对角线吗?试着在几何图纸上画出
2
5
9
太难画了,能不全画出对角线而计算出来吗?
你能告诉我二十边形的对角线条数吗?五十边形呢?一百边形呢?n边形呢?
从四边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从五边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
从六边形的一个顶点出发,可以引 条对角线,共有_____条对角线;
一
两
三
从n边形的一个顶点出发,可以引 __条对角线,共有 条对角线. (n≥3且为整数)
(n-3)
(1)
(2)
(3)
…
两
五
九
思考:
今后如果不作说明,我们说的多边形都是凸多边形.
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
图 1
A
C
B
D
图 2
A
C
B
D
探索四边形的内角和
A
D
C
B
二、动手操作,探索新知
试着在几何图纸上用不同方法求四边形内角和
以四边形为例:
探究多边形内角和还有哪些方法?
D
C
B
A
O
D
C
B
A
O
D
C
B
A
O
●
●
●
3×180°-180°
=360°
4×180°-360°
=360°
3×180°-180°
=360°
共同点:找一个点,将四边形转化为三角形。
D
C
B
A
探索五边形的内角和
A
B
C
D
E
类比四边形求内角和,试着在几何图纸上用不同方法求五边形内角和
E
A
B
C
D
.
O
180°×5 - 360° = 540°
A
B
C
D
E
F
180°×4 -180° =540°
共同点:找一个点,将五边形转化为三角形。
探索六边形的内角和
A
B
C
D
E
F
小组讨论探究:选取最佳方法求六边形内角和
180°×4=720°
归纳总结
多边形边数 从一个顶点引出对角线条数 图形 分割成的三角形个数
多边形的内角和
4
5
6
... …… …… …… ……
n
2
2×1800
3
3×1800
4
4×1800
n-2
(n-2)×1800
1
2
3
n-3
探索n边形的内角和
①n代表什么?
② n-2表示什么含义?
③为什么要乘以180°
定理:n边形内角和公式为:______________________________。
(n-2)·180°(n≥3且为整数)
例:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
三、初步应用,感悟新知
变式练习1:已知一个多边形的内角和是2160°,
求它的边数。
解 : 设这个多边形有n条边.由多边形内角和定理知:
即这个多边形有14条边.
(n-2) ×180°=2160°
得 n =14
四、巩固练习
变式练习2:有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
M
N
解:
①三角形,内角和为180°
②四边形,内角和为360°
③五边形,内角和为540°
多边形
分割成三角形
多边形的内角和
转化
归纳
(n-2) · 180°(n ≥3且为整数)
1.多边形有关概念(边、顶点、内角、外角、对角线)
2.
五、课堂小结
3、数学问题的思想方法:如将多边形问题转化为三角形问题,以及类比法、归纳法、分类的思想方法。
谢 谢
