沪科版数学八年级下册 17.5 一元二次方程的应用 课件(共21张)
文档属性
| 名称 | 沪科版数学八年级下册 17.5 一元二次方程的应用 课件(共21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 429.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 16:36:03 | ||
图片预览







文档简介
(共21张PPT)
17.5 一元二次方程的应用
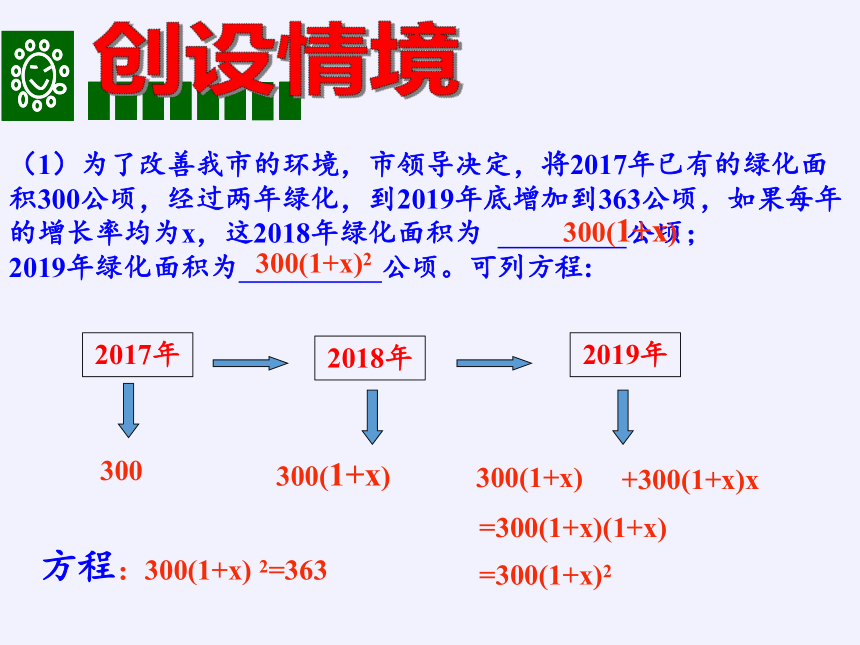
(1)为了改善我市的环境,市领导决定,将2017年已有的绿化面积300公顷,经过两年绿化,到2019年底增加到363公顷,如果每年的增长率均为x,这2018年绿化面积为 公顷;
2019年绿化面积为 公顷。可列方程:
300(1+x)
=300(1+x)2
方程:300(1+x) 2=363
2017年
2019年
2018年
300
300(1+x)
300(1+x)2
创设情境
300(1+x)
=300(1+x)(1+x)
+300(1+x)x
(2)华松国际有一种毛衣从原来的每件400元,经两次调价后,调至每件320.4元,若两次调价的降价率均为x,则第一次调价后降至 元,第二次调价后降至 元。
可列方程为:
400(1-x)
400(1-x)2
400(1-x)2=320.4
这两道应用题有什么共同特点
特点:
1.都是两次增长(降低)
2.增长(降低)率相同
3.都有一个初始量
4.都有一个最终变化量
1111
一元二次方程的应用(增长率问题)
400(1-x)2=320.4
300(1+x) 2=363
观察下列两个方程,回答以下问题:
1.以上两个方程是哪种性质的方程?
2.这两个方程有什么共同特点?
3.解这类方程用那种方法最好?
1.两次平均增长(降低)率公式
2.注意:
(1) a表示初量,b 表示末量,x表示增长 率(降低率),2表示增长次数
(2)1与x的位置不要调换
(3)解这类问题列出的方程一般
用 直接开平方法
智慧结晶
400(1-x)2=320.4
某工厂1月份的产值是50000元,3月份的产值达到60500元,这两个月的产值平均每月增长的百分率是多少?
解:这两个月的产值平均每月增长的百分率是x,
50000 (1+x) 2 =60500
(1+x) 2 =1.21
x1 0.1= 10%, x2 2.2(不符合题意,舍去)
答:平均每月增长的百分率为10% .
小试牛刀
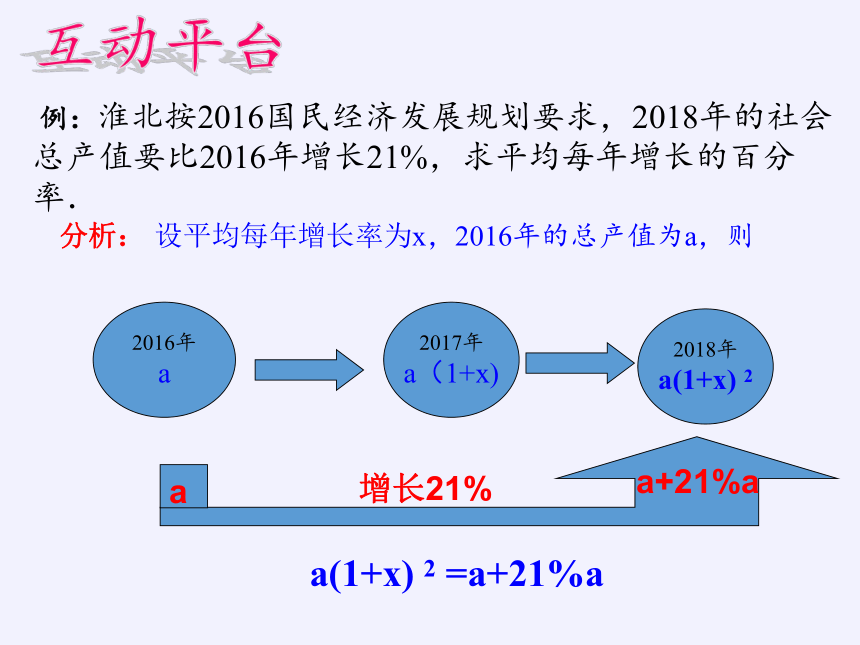
例:淮北按2016国民经济发展规划要求,2018年的社会总产值要比2016年增长21%,求平均每年增长的百分率.
设平均每年增长率为x,2016年的总产值为a,则
2016年
a
2017年
a(1+x)
2018年
a(1+x) 2
增长21%
a
a+21%a
a(1+x) 2 =a+21%a
分析:
互动平台
正确解法:a (1+x) 2 =1.21 a
(1+x) 2 =1.21
x1 0.1, x2 2.2(不符合题意,舍去)
解:设每年增长率为x,2001年的总产值为a,则
a(1+x) 2 =a+21%a
答:平均每年增长的百分率为10% .
a (1+x) 2 =1.21 a
(1+x) 2 =1.21
x1 0.1,
答:平均每年增长的百分率为10% .
错误解法:
(1+x) 2 =1.21
1+x =+1.1
x1 0.1, x2 2.2(不符合题意,舍去)
解:设每年增长率为x,2001年的总产值为1,
则
(1+x) 2 =1+21%
答:平均每年增长的百分率为10% .
方法二
1. 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析
1
第一轮传染后
1+x
第二轮传染后
(1+x)+x(1+x)
= (1+x)2
解:设每轮传染中平均一个人传染了x个人.
开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_____人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,
用代数式表示,第二轮后共有____________人患了流感.
(x+1)
1+x+x(1+x)
=(1+x )2
(1+x)+x(1+x)=121 即(1+x)2=121
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去)
10
通过对这个问题的
探究,你对类似的传播
问题中的数量关系有
新的认识吗
探索乐园
--------变式1
如果按照这样的传染速度,
三轮传染后有多少人患流感
N轮后呐
方法二:121+121×10=1331人
N轮后:(1+10)n
方法一:(1+10)3=1331人
1.若原来量(初量)为a,平均增长率是x,增长后的量(末量)为b ,n为增长次数。
则 第1次增长后的量是a(1+x) =b
第2次增长后的量是a(1+x)2=b
……
第n次增长后的量是a(1+x)n=b
这就是重要的增长率公式.
2、特别地,两次平均增长(降低)率公 式为
智慧升华
某公司制作了一则电子广告,为鼓励员工利用微信进行传播,特制定以下规则:首先由员工将广告链接发送在自己的朋友圈,再邀请n(n为整数)个好友转发,每个好友转发后,又邀请n个互不相同的好友转发,依次类推,如果n>10,且至少传播两轮,则该员工将获得10n元钱的奖金,经调查发现,员工小李经过两轮传播之后共有421人参与了活动,则他可获得奖金多少元?
探索乐园
变式2------传播问题2
解:由题意得 : 1+n+n2=421
解得; n1=20, n2= -21
因为n>10 所以 n=20
故10n=10x20=200
答:小李可获得奖金100元 。
1.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程中正确的是( )
A.
C.
C
2.某厂今年一月的总产量为500吨,三月的总产量 为720吨,平均每月增长率是x,列方程( .某厂今年一月的总产量为500吨,三月的总产量 为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
B
才艺展示
B.
D.
3.党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两翻。在本世纪的头20年(2001年~2020年)要实现这一目标,以10年为单位计算,设每个10年的国民生产总值的增长率都是x,根据题意得方程为( )
A. B.
C. 1+2x=2 D.(1+x)+2(1+x)=4
B
4、某农场粮食产量是:2003年1200万千克,2004年为1452万千克。如果平均每年的增长率为x,则可得方程( )
A. 1200(1+x) =1452 B. 1200(1+2x)=1452
C. 1200(1+x%)2=1452 D. 1200(1+x%)=14
5、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均月增长率为x,则可列方程为 ( )
200(1+x)2=1000 B. 200+200×2×x=1000
C.200+200×3×x=1000 D. 200+200(1+x)+ 200(1+x)2=1000
6、某种植物主干长出若干数目的枝干,每个分枝又长出同样数目的小分支,主干枝干小分支的总数是91 ,每个枝干长出几个小分支?是每个枝干长出x个小分支。( )
A.(1+x)2=91 B. 1+x+x2=91
C. 1+x+2x=91 D. 1+2x+x2=91
A
D
B
一展身手
1.某校去年对实验器材的投资为2万元,预计今年和明年两年的投资总额为8万元,若设该校今年和明年两年在实验器材投资上的平均增长率是x,则可列方程为_______________
2、某商场二月份的销售额为100万元,三月份的销售额下降了20%,商场从四月份起改进经营措施,销售额稳步增长,五月份销售额达到135.2万元,求四、五两个月的平均增长率。
则可列方程为_______________
经历今天的学习活动,你有何收获和体会,请把你的感悟告诉你的同学!
畅所欲言
教师感悟:
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
方程的应用是解决生活实际问题的重要工具。一份耕耘、一份收获,同学们相信自己,只要付出,一定会有收获!会有解决以上问题的方法!行动吧!
谢 谢
17.5 一元二次方程的应用
(1)为了改善我市的环境,市领导决定,将2017年已有的绿化面积300公顷,经过两年绿化,到2019年底增加到363公顷,如果每年的增长率均为x,这2018年绿化面积为 公顷;
2019年绿化面积为 公顷。可列方程:
300(1+x)
=300(1+x)2
方程:300(1+x) 2=363
2017年
2019年
2018年
300
300(1+x)
300(1+x)2
创设情境
300(1+x)
=300(1+x)(1+x)
+300(1+x)x
(2)华松国际有一种毛衣从原来的每件400元,经两次调价后,调至每件320.4元,若两次调价的降价率均为x,则第一次调价后降至 元,第二次调价后降至 元。
可列方程为:
400(1-x)
400(1-x)2
400(1-x)2=320.4
这两道应用题有什么共同特点
特点:
1.都是两次增长(降低)
2.增长(降低)率相同
3.都有一个初始量
4.都有一个最终变化量
1111
一元二次方程的应用(增长率问题)
400(1-x)2=320.4
300(1+x) 2=363
观察下列两个方程,回答以下问题:
1.以上两个方程是哪种性质的方程?
2.这两个方程有什么共同特点?
3.解这类方程用那种方法最好?
1.两次平均增长(降低)率公式
2.注意:
(1) a表示初量,b 表示末量,x表示增长 率(降低率),2表示增长次数
(2)1与x的位置不要调换
(3)解这类问题列出的方程一般
用 直接开平方法
智慧结晶
400(1-x)2=320.4
某工厂1月份的产值是50000元,3月份的产值达到60500元,这两个月的产值平均每月增长的百分率是多少?
解:这两个月的产值平均每月增长的百分率是x,
50000 (1+x) 2 =60500
(1+x) 2 =1.21
x1 0.1= 10%, x2 2.2(不符合题意,舍去)
答:平均每月增长的百分率为10% .
小试牛刀
例:淮北按2016国民经济发展规划要求,2018年的社会总产值要比2016年增长21%,求平均每年增长的百分率.
设平均每年增长率为x,2016年的总产值为a,则
2016年
a
2017年
a(1+x)
2018年
a(1+x) 2
增长21%
a
a+21%a
a(1+x) 2 =a+21%a
分析:
互动平台
正确解法:a (1+x) 2 =1.21 a
(1+x) 2 =1.21
x1 0.1, x2 2.2(不符合题意,舍去)
解:设每年增长率为x,2001年的总产值为a,则
a(1+x) 2 =a+21%a
答:平均每年增长的百分率为10% .
a (1+x) 2 =1.21 a
(1+x) 2 =1.21
x1 0.1,
答:平均每年增长的百分率为10% .
错误解法:
(1+x) 2 =1.21
1+x =+1.1
x1 0.1, x2 2.2(不符合题意,舍去)
解:设每年增长率为x,2001年的总产值为1,
则
(1+x) 2 =1+21%
答:平均每年增长的百分率为10% .
方法二
1. 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析
1
第一轮传染后
1+x
第二轮传染后
(1+x)+x(1+x)
= (1+x)2
解:设每轮传染中平均一个人传染了x个人.
开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有_____人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,
用代数式表示,第二轮后共有____________人患了流感.
(x+1)
1+x+x(1+x)
=(1+x )2
(1+x)+x(1+x)=121 即(1+x)2=121
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去)
10
通过对这个问题的
探究,你对类似的传播
问题中的数量关系有
新的认识吗
探索乐园
--------变式1
如果按照这样的传染速度,
三轮传染后有多少人患流感
N轮后呐
方法二:121+121×10=1331人
N轮后:(1+10)n
方法一:(1+10)3=1331人
1.若原来量(初量)为a,平均增长率是x,增长后的量(末量)为b ,n为增长次数。
则 第1次增长后的量是a(1+x) =b
第2次增长后的量是a(1+x)2=b
……
第n次增长后的量是a(1+x)n=b
这就是重要的增长率公式.
2、特别地,两次平均增长(降低)率公 式为
智慧升华
某公司制作了一则电子广告,为鼓励员工利用微信进行传播,特制定以下规则:首先由员工将广告链接发送在自己的朋友圈,再邀请n(n为整数)个好友转发,每个好友转发后,又邀请n个互不相同的好友转发,依次类推,如果n>10,且至少传播两轮,则该员工将获得10n元钱的奖金,经调查发现,员工小李经过两轮传播之后共有421人参与了活动,则他可获得奖金多少元?
探索乐园
变式2------传播问题2
解:由题意得 : 1+n+n2=421
解得; n1=20, n2= -21
因为n>10 所以 n=20
故10n=10x20=200
答:小李可获得奖金100元 。
1.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程中正确的是( )
A.
C.
C
2.某厂今年一月的总产量为500吨,三月的总产量 为720吨,平均每月增长率是x,列方程( .某厂今年一月的总产量为500吨,三月的总产量 为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
B
才艺展示
B.
D.
3.党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两翻。在本世纪的头20年(2001年~2020年)要实现这一目标,以10年为单位计算,设每个10年的国民生产总值的增长率都是x,根据题意得方程为( )
A. B.
C. 1+2x=2 D.(1+x)+2(1+x)=4
B
4、某农场粮食产量是:2003年1200万千克,2004年为1452万千克。如果平均每年的增长率为x,则可得方程( )
A. 1200(1+x) =1452 B. 1200(1+2x)=1452
C. 1200(1+x%)2=1452 D. 1200(1+x%)=14
5、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均月增长率为x,则可列方程为 ( )
200(1+x)2=1000 B. 200+200×2×x=1000
C.200+200×3×x=1000 D. 200+200(1+x)+ 200(1+x)2=1000
6、某种植物主干长出若干数目的枝干,每个分枝又长出同样数目的小分支,主干枝干小分支的总数是91 ,每个枝干长出几个小分支?是每个枝干长出x个小分支。( )
A.(1+x)2=91 B. 1+x+x2=91
C. 1+x+2x=91 D. 1+2x+x2=91
A
D
B
一展身手
1.某校去年对实验器材的投资为2万元,预计今年和明年两年的投资总额为8万元,若设该校今年和明年两年在实验器材投资上的平均增长率是x,则可列方程为_______________
2、某商场二月份的销售额为100万元,三月份的销售额下降了20%,商场从四月份起改进经营措施,销售额稳步增长,五月份销售额达到135.2万元,求四、五两个月的平均增长率。
则可列方程为_______________
经历今天的学习活动,你有何收获和体会,请把你的感悟告诉你的同学!
畅所欲言
教师感悟:
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。
方程的应用是解决生活实际问题的重要工具。一份耕耘、一份收获,同学们相信自己,只要付出,一定会有收获!会有解决以上问题的方法!行动吧!
谢 谢
