沪科版数学八年级下册 19.2平行四边形性质 课件(共16张)
文档属性
| 名称 | 沪科版数学八年级下册 19.2平行四边形性质 课件(共16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 16:41:04 | ||
图片预览

文档简介
(共16张PPT)
19.2 平行四边形
平行四边形性质3
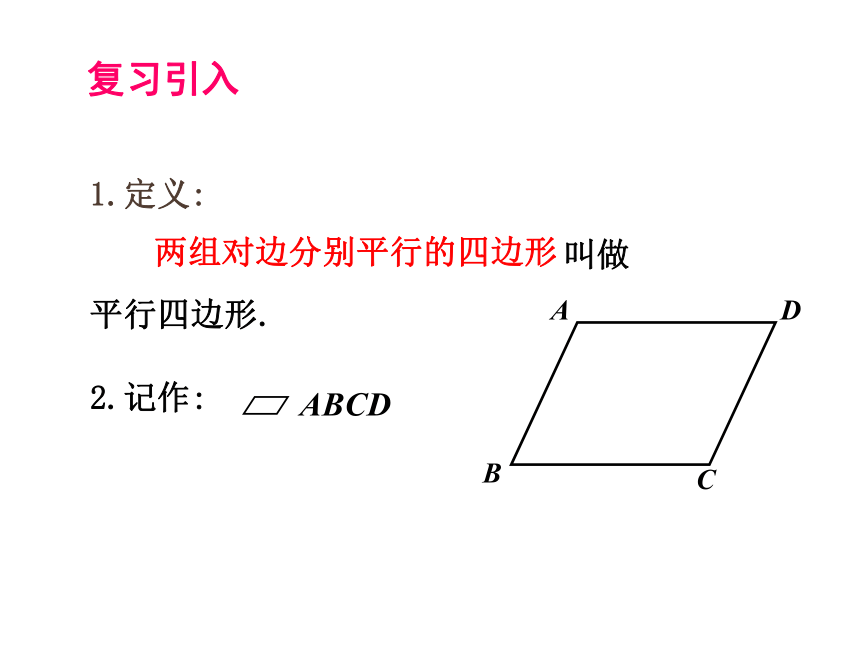
1.定义:
叫做
平行四边形.
2.记作:
ABCD
A
B
C
D
复习引入
两组对边分别平行的四边形
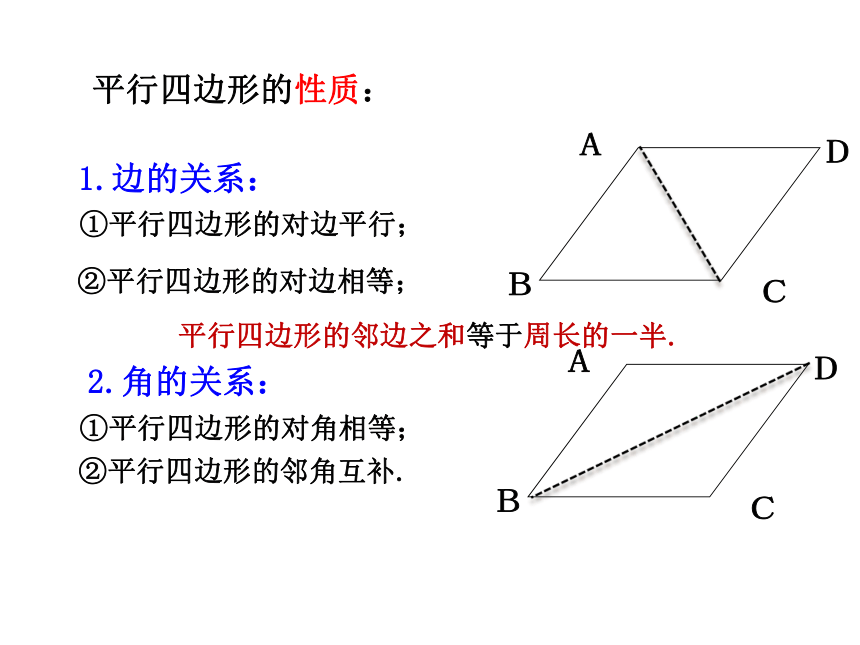
平行四边形的性质:
①平行四边形的对边平行;
①平行四边形的对角相等;
1.边的关系:
2.角的关系:
②平行四边形的对边相等;
平行四边形的邻边之和等于周长的一半.
②平行四边形的邻角互补.
O
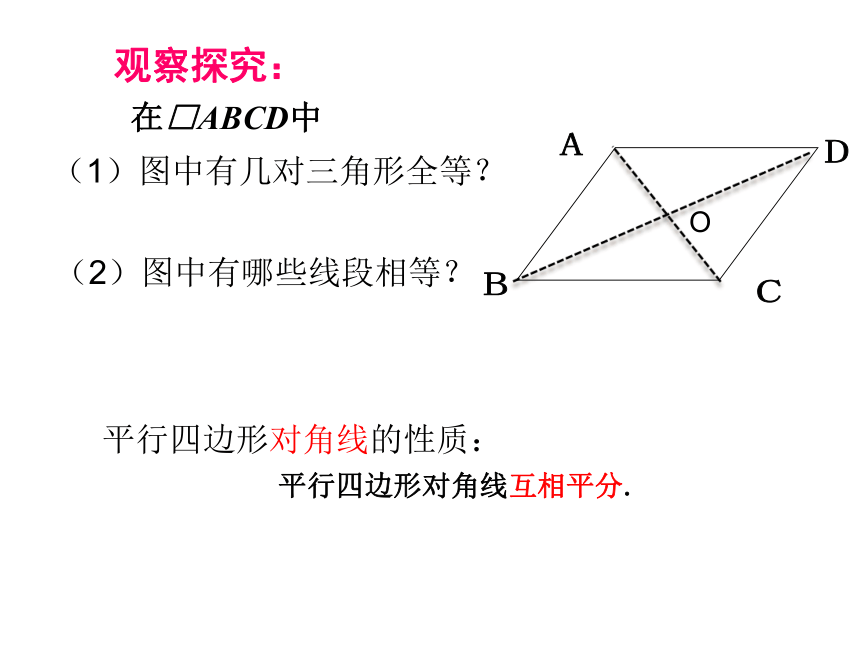
(1)图中有几对三角形全等?
(2)图中有哪些线段相等?
观察探究:
平行四边形对角线的性质:
平行四边形对角线互相平分.
在□ABCD中
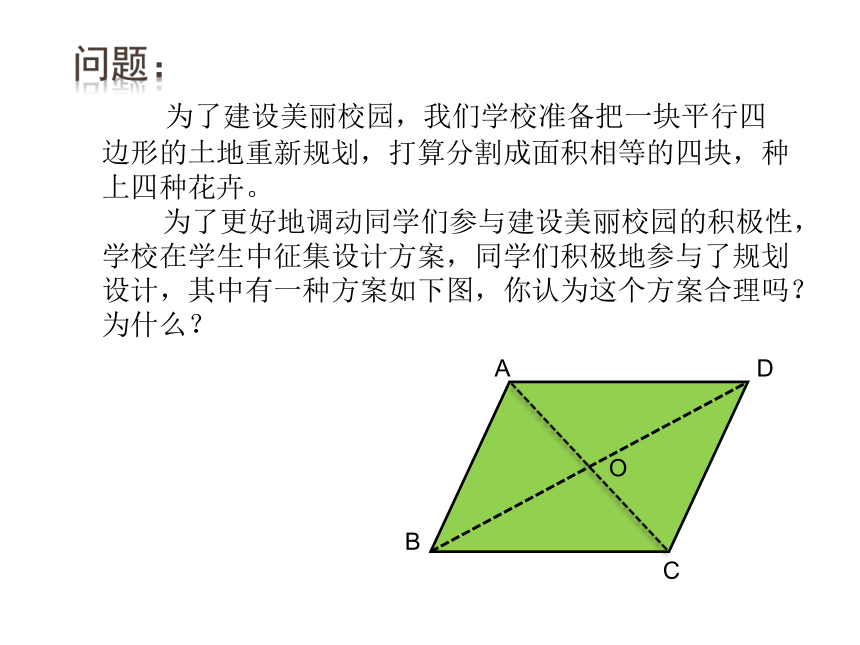
为了建设美丽校园,我们学校准备把一块平行四边形的土地重新规划,打算分割成面积相等的四块,种上四种花卉。
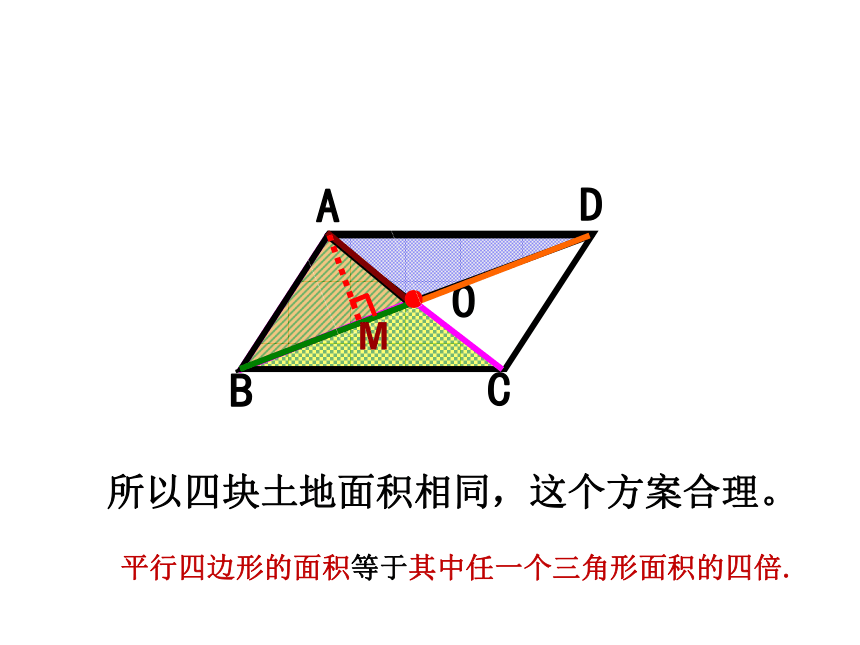
为了更好地调动同学们参与建设美丽校园的积极性,学校在学生中征集设计方案,同学们积极地参与了规划设计,其中有一种方案如下图,你认为这个方案合理吗?为什么?
A
O
D
C
B
A
C
D
B
O
●
M
所以四块土地面积相同,这个方案合理。
平行四边形的面积等于其中任一个三角形面积的四倍.
①平行四边形的对边平行;
①平行四边形的对角相等;
1.边的关系:
2.角的关系:
②平行四边形的对边相等;
平行四边形的邻边之和等于周长的一半.
②平行四边形的邻角互补.
3.对角线的关系:
平行四边形对角线互相平分.
O
平行四边形的面积等于其中任一个三角形面积的四倍.
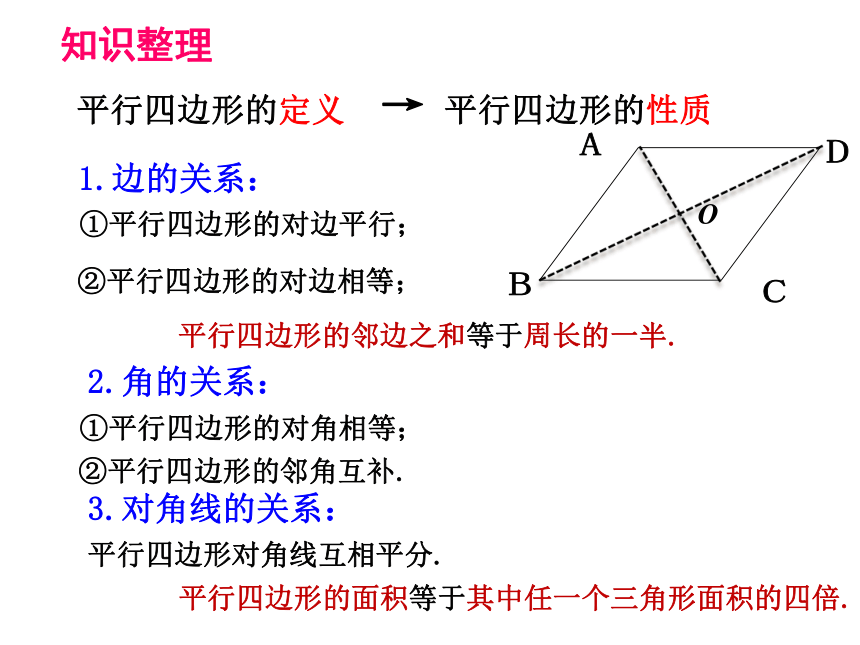
知识整理
平行四边形的定义 → 平行四边形的性质
例1.如图,在□ABCD中,对角线AC、BD相
交于点O,△ABO的面积为6,则图中阴影部
分的面积为 .
学以致用
牛刀小试
12
例2. (1)如图,在□ABCD中,AC、BD相交于点O.已知BC=10,AC=8,BD=14,则△AOD的周长是 ;
21
火眼金睛
学以致用
例2. (2)如图,在□ABCD中,AC、BD相交于点O.已知AB=5,BC=10,则△BCO 比△DCO的周长大 .
5
火眼金睛
△BCO 与△DCO的周长之差即为BC与CD之差.
学以致用
小结一下:
例3. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5.
(1)求AC的长.
解:(1)
∵四边形ABCD是平行四边形
∴BC=AD=5
∴AB⊥AC
∴△ABC是直角三角形
勇攀高峰
学以致用
例3. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5.
(1)求AC的长. (2)求BD的长.
解:(2)
AO= AC=2
∴BD=2BO=
∴
勇攀高峰
由(1)得AC=4
∴
如图,在□ABCD中,对角线AC与BD互相
垂直,那么,这个四边形的邻边有什么关系,
为什么?
跟踪练习
通过本节课的学习,你有什么收获?
平行四边形的定义 → 平行四边形的性质
课堂小结
1.边的关系:
①平行四边形的对边平行;
②平行四边形的对边相等;
2.角的关系:
①平行四边形的对角相等;
②平行四边形的邻角互补.
3.对角线的关系:
平行四边形的对角线互相平分.
布置作业:
酌情完成学案后的补充习题,及课本练习题1.
19.2 平行四边形
平行四边形性质3
1.定义:
叫做
平行四边形.
2.记作:
ABCD
A
B
C
D
复习引入
两组对边分别平行的四边形
平行四边形的性质:
①平行四边形的对边平行;
①平行四边形的对角相等;
1.边的关系:
2.角的关系:
②平行四边形的对边相等;
平行四边形的邻边之和等于周长的一半.
②平行四边形的邻角互补.
O
(1)图中有几对三角形全等?
(2)图中有哪些线段相等?
观察探究:
平行四边形对角线的性质:
平行四边形对角线互相平分.
在□ABCD中
为了建设美丽校园,我们学校准备把一块平行四边形的土地重新规划,打算分割成面积相等的四块,种上四种花卉。
为了更好地调动同学们参与建设美丽校园的积极性,学校在学生中征集设计方案,同学们积极地参与了规划设计,其中有一种方案如下图,你认为这个方案合理吗?为什么?
A
O
D
C
B
A
C
D
B
O
●
M
所以四块土地面积相同,这个方案合理。
平行四边形的面积等于其中任一个三角形面积的四倍.
①平行四边形的对边平行;
①平行四边形的对角相等;
1.边的关系:
2.角的关系:
②平行四边形的对边相等;
平行四边形的邻边之和等于周长的一半.
②平行四边形的邻角互补.
3.对角线的关系:
平行四边形对角线互相平分.
O
平行四边形的面积等于其中任一个三角形面积的四倍.
知识整理
平行四边形的定义 → 平行四边形的性质
例1.如图,在□ABCD中,对角线AC、BD相
交于点O,△ABO的面积为6,则图中阴影部
分的面积为 .
学以致用
牛刀小试
12
例2. (1)如图,在□ABCD中,AC、BD相交于点O.已知BC=10,AC=8,BD=14,则△AOD的周长是 ;
21
火眼金睛
学以致用
例2. (2)如图,在□ABCD中,AC、BD相交于点O.已知AB=5,BC=10,则△BCO 比△DCO的周长大 .
5
火眼金睛
△BCO 与△DCO的周长之差即为BC与CD之差.
学以致用
小结一下:
例3. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5.
(1)求AC的长.
解:(1)
∵四边形ABCD是平行四边形
∴BC=AD=5
∴AB⊥AC
∴△ABC是直角三角形
勇攀高峰
学以致用
例3. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5.
(1)求AC的长. (2)求BD的长.
解:(2)
AO= AC=2
∴BD=2BO=
∴
勇攀高峰
由(1)得AC=4
∴
如图,在□ABCD中,对角线AC与BD互相
垂直,那么,这个四边形的邻边有什么关系,
为什么?
跟踪练习
通过本节课的学习,你有什么收获?
平行四边形的定义 → 平行四边形的性质
课堂小结
1.边的关系:
①平行四边形的对边平行;
②平行四边形的对边相等;
2.角的关系:
①平行四边形的对角相等;
②平行四边形的邻角互补.
3.对角线的关系:
平行四边形的对角线互相平分.
布置作业:
酌情完成学案后的补充习题,及课本练习题1.
