沪科版数学八年级下册 18.1 勾股定理 教案
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 263.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 19:37:37 | ||
图片预览

文档简介
18.1勾股定理
教学目标:
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景;会用面积法来证明勾股定理,体会数形结合的思想;
2.会用勾股定理进行简单的计算;
3.通过对勾股定理历史的了解,对比介绍我国古代和西方数学家关于勾股定理的研究,激发学生热爱祖国悠久文化的情感,激励学生奋发学习。
二.教学重点:
会用面积法来证明勾股定理,体会数形结合的思想;
三.教学难点:
会用勾股定理进行简单的计算;
四.教学过程:
(一)复习回顾,导入新课:
在小学,我们已经认识了三角形,现在请同学们来谈谈你对三角形的了解。
直角三角形是特殊的三角形,直角三角形的三个内角在满足一般三角形的三个内角和是1800以外,是否还有其特殊性呢?因此,我提出这样的疑问:直角三角形的边在满足任意两边之和大于第三边以外,是否还具备特殊性呢?这就是这节课我们要研究的内容——勾股定理。(板书课题)
探索新知:
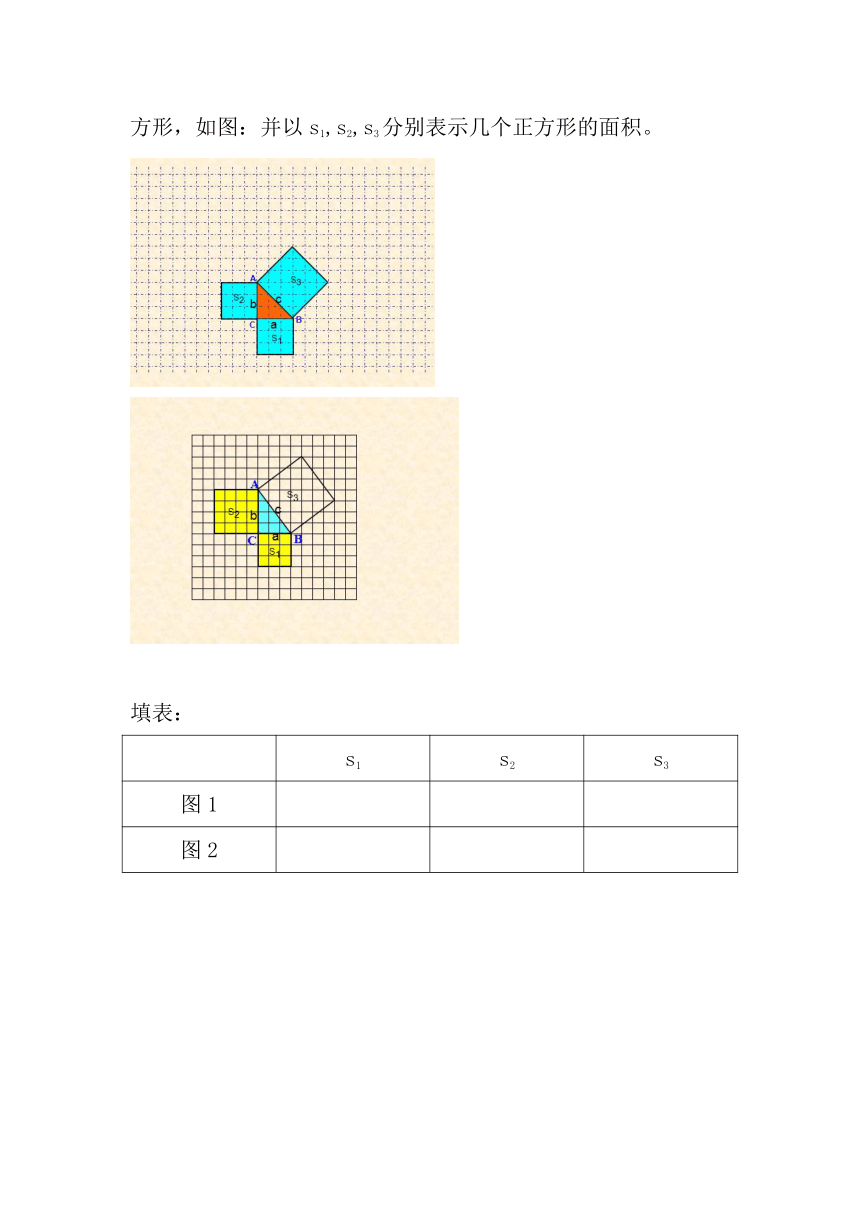
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图:并以s1,s2,s3分别表示几个正方形的面积。
填表:
s1 s2 s3
图1
图2
猜想命题:
命题:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
验证猜想:
请以小组为单位拿出准备好的四个全等三角形尝试拼出“赵爽弦图”吗?
2000多年前,汉代数学家赵爽就用这个图形验证了我们的猜想,我们现在能否也用这个图形验证我们的猜想呢?
(五)得出定理:
勾股定理:
文字语言:直角三角形两直角边的平方和等于斜边的平方。
符号语言:在Rt△ABC中,∠C=90°, AC2+BC2= AB2 (或a2+b2=c2)
我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。因此就把这一关于直角三角形三边关系的定理称为勾股定理。
我国是最早了角勾股定理的国家之一,早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
强调:勾股定理仅仅适用于直角三角形。。
应用定理:
教学目标:
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景;会用面积法来证明勾股定理,体会数形结合的思想;
2.会用勾股定理进行简单的计算;
3.通过对勾股定理历史的了解,对比介绍我国古代和西方数学家关于勾股定理的研究,激发学生热爱祖国悠久文化的情感,激励学生奋发学习。
二.教学重点:
会用面积法来证明勾股定理,体会数形结合的思想;
三.教学难点:
会用勾股定理进行简单的计算;
四.教学过程:
(一)复习回顾,导入新课:
在小学,我们已经认识了三角形,现在请同学们来谈谈你对三角形的了解。
直角三角形是特殊的三角形,直角三角形的三个内角在满足一般三角形的三个内角和是1800以外,是否还有其特殊性呢?因此,我提出这样的疑问:直角三角形的边在满足任意两边之和大于第三边以外,是否还具备特殊性呢?这就是这节课我们要研究的内容——勾股定理。(板书课题)
探索新知:
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图:并以s1,s2,s3分别表示几个正方形的面积。
填表:
s1 s2 s3
图1
图2
猜想命题:
命题:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
验证猜想:
请以小组为单位拿出准备好的四个全等三角形尝试拼出“赵爽弦图”吗?
2000多年前,汉代数学家赵爽就用这个图形验证了我们的猜想,我们现在能否也用这个图形验证我们的猜想呢?
(五)得出定理:
勾股定理:
文字语言:直角三角形两直角边的平方和等于斜边的平方。
符号语言:在Rt△ABC中,∠C=90°, AC2+BC2= AB2 (或a2+b2=c2)
我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。因此就把这一关于直角三角形三边关系的定理称为勾股定理。
我国是最早了角勾股定理的国家之一,早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
强调:勾股定理仅仅适用于直角三角形。。
应用定理:
