冀教版数学七年级上册 1.12计算器的使用 同步课件(共14张PPT)
文档属性
| 名称 | 冀教版数学七年级上册 1.12计算器的使用 同步课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第一章 有理数
1.12 计算器的使用
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感激谢,国王答应满足这个大臣的一个要求.
大臣说:“就在这个棋盘里放些米粒吧.第一个格放1粒米,第二格放2粒米,以后每一格是前一格米粒数的2倍……一直到第64格.”
国王哈哈大笑,“你真傻,就要这么一点米粒?”
大臣说:“就怕您的国库里没有这么多大米!”
国王的国库有这么多米吗?
情景导入
获取新知
一起探究
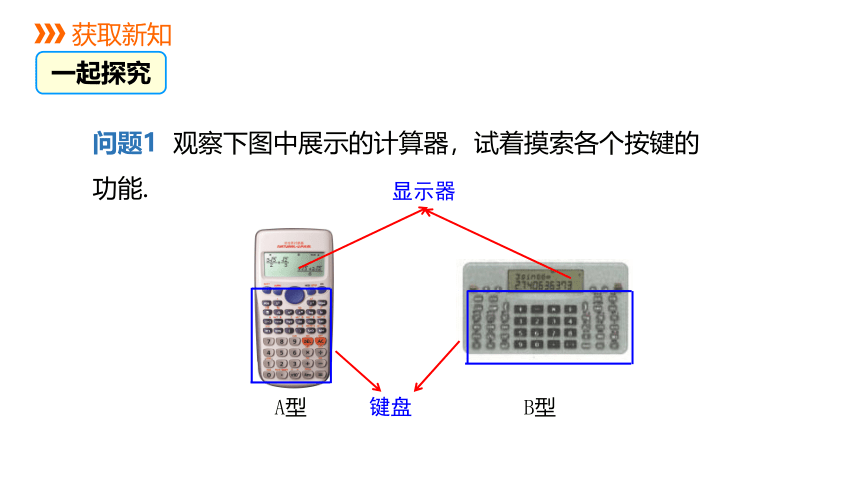
问题1 观察下图中展示的计算器,试着摸索各个按键的功能.
A型
B型
显示器
键盘
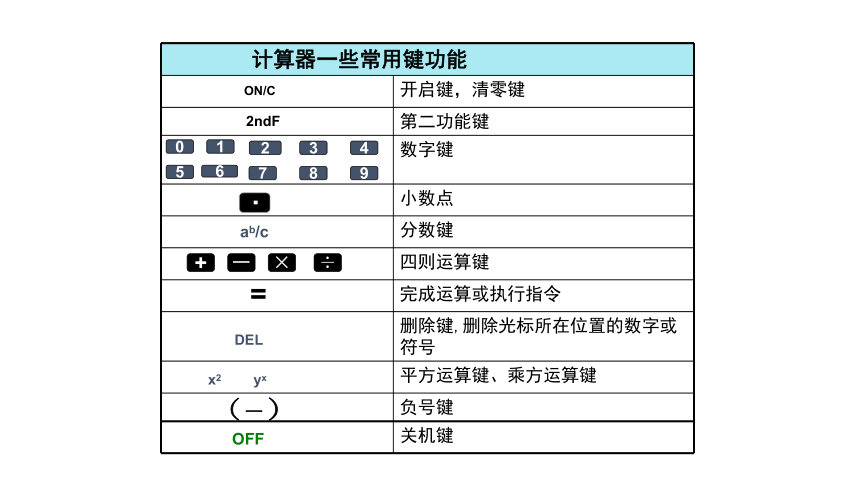
计算器一些常用键功能 开启键,清零键
第二功能键
数字键
小数点
分数键
四则运算键
完成运算或执行指令
删除键,删除光标所在位置的数字或符号
平方运算键、乘方运算键
负号键
关机键
0
1
2
3
5
6
7
8
4
9
ab/c
+
-
×
÷
=
DEL
OFF
ON/C
2ndF
yx
x2
(-)
试一试
你知道怎么在计算器上按出下列数字吗?
A,B两种型号的计算器的按键顺序为
2
5
ab/c
4
x2
5
yx
4
(-)
2
5
x2
1
ab/c
3
ab/c
4
例1 用计算器计算:
(1)-125÷5-15×(-3); (2)-1.32+1.24.
解:(1)-125÷5-15×(-3),
A,B两种型号的计算器的按键顺序为
显示器显示的结果为20,所以-125÷5-15×(-3)=20.
(2)-1.32+1.24,A,B两种型号的计算器的按键顺序为
(-)
1
3
x2
1
2
yx
4
=
+
(-)
1
2
5
5
3
=
1
5
(-)
÷
×
-
显示器显示的结果为0.383 6,所以-1.32+1.24=0.383 6.
例题讲解
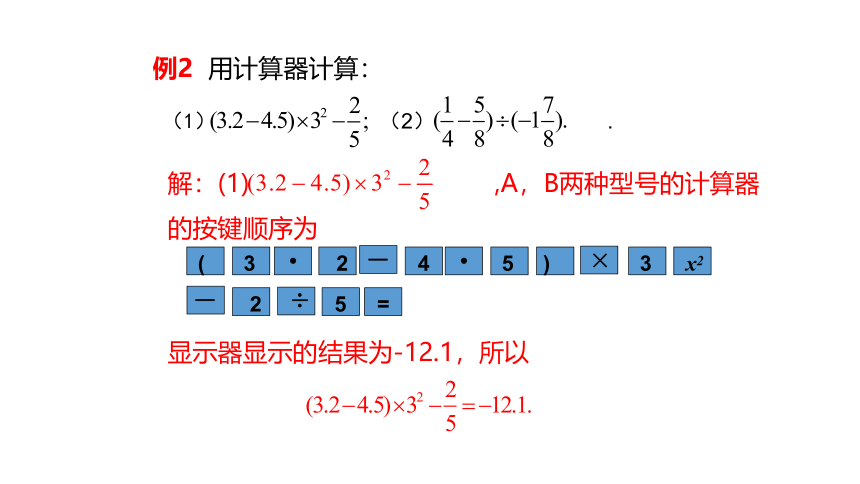
例2 用计算器计算:
(1) (2) .
解:(1) ,A,B两种型号的计算器的按键顺序为
×
)
-
-
(
3
2
4
5
3
2
5
=
x2
÷
显示器显示的结果为-12.1,所以
(2) ,A,B两种型号的计算器的按键顺序为
(-)
7
1
=
(
1
ab/c
4
-
5
ab/c
8
)
÷
ab/c
ab/c
8
A型计算器显示的结果为 ,B型计算器显示的结果为
,所以
1
5
1
5
算出 后,如果继续按 键,就将分数转化成了小数的表示形式.
ab/c
再将结果四舍五入后就可以得到答案1.374.
利用计算器探索规律
步骤:
1.任选1,2,3,4,5,6,7,8,9中的一个数
2.将这个数字乘以9
3.将上面的结果乘以12 345 679
多选几个数试一试,你发现了什么规律?与同伴交流你的理由.
获取新知
一起探究
你从这些计算结果中发现了什么规律?
问题3 写出一个四位数,它的各个数位上的数字各不相等(如6731),用这个四位数各个数位上的数字组成一个最大数和一个最小数,并用最大数减去最小数,得到一个新的四位数,重复上面的过程,又得到一个新的四位数.一直重复下去,你发现了什么?请借助计算器帮助你进行探索.
“黑洞”数:6174
1. 利用计算器计算(说明按键方法及运算结果.
解:(1) 0;(2) 4;(3) 2 (4) -3.
2. 若按键顺序为: ,则与其对应的算式是______________.
(-)
3
x2
2
yx
4
=
+
随堂演练
1 ×1=_____;11 ×11=_______; 111 ×111=_________.
3.用计算器探索:
(1)用计算器计算:
(2)根据(1)的计算结果,总结规律,不用计算器,试直接写出下列式子的答案.
1111 ×1111=_________; 111111×111111=____________;
111111111×111111111=___________________.
1
121
12321
1234321
12345654321
12345678987654321
计算器的使用
利用计算器计算
利用计算器探索规律
课堂小结
第一章 有理数
1.12 计算器的使用
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感激谢,国王答应满足这个大臣的一个要求.
大臣说:“就在这个棋盘里放些米粒吧.第一个格放1粒米,第二格放2粒米,以后每一格是前一格米粒数的2倍……一直到第64格.”
国王哈哈大笑,“你真傻,就要这么一点米粒?”
大臣说:“就怕您的国库里没有这么多大米!”
国王的国库有这么多米吗?
情景导入
获取新知
一起探究
问题1 观察下图中展示的计算器,试着摸索各个按键的功能.
A型
B型
显示器
键盘
计算器一些常用键功能 开启键,清零键
第二功能键
数字键
小数点
分数键
四则运算键
完成运算或执行指令
删除键,删除光标所在位置的数字或符号
平方运算键、乘方运算键
负号键
关机键
0
1
2
3
5
6
7
8
4
9
ab/c
+
-
×
÷
=
DEL
OFF
ON/C
2ndF
yx
x2
(-)
试一试
你知道怎么在计算器上按出下列数字吗?
A,B两种型号的计算器的按键顺序为
2
5
ab/c
4
x2
5
yx
4
(-)
2
5
x2
1
ab/c
3
ab/c
4
例1 用计算器计算:
(1)-125÷5-15×(-3); (2)-1.32+1.24.
解:(1)-125÷5-15×(-3),
A,B两种型号的计算器的按键顺序为
显示器显示的结果为20,所以-125÷5-15×(-3)=20.
(2)-1.32+1.24,A,B两种型号的计算器的按键顺序为
(-)
1
3
x2
1
2
yx
4
=
+
(-)
1
2
5
5
3
=
1
5
(-)
÷
×
-
显示器显示的结果为0.383 6,所以-1.32+1.24=0.383 6.
例题讲解
例2 用计算器计算:
(1) (2) .
解:(1) ,A,B两种型号的计算器的按键顺序为
×
)
-
-
(
3
2
4
5
3
2
5
=
x2
÷
显示器显示的结果为-12.1,所以
(2) ,A,B两种型号的计算器的按键顺序为
(-)
7
1
=
(
1
ab/c
4
-
5
ab/c
8
)
÷
ab/c
ab/c
8
A型计算器显示的结果为 ,B型计算器显示的结果为
,所以
1
5
1
5
算出 后,如果继续按 键,就将分数转化成了小数的表示形式.
ab/c
再将结果四舍五入后就可以得到答案1.374.
利用计算器探索规律
步骤:
1.任选1,2,3,4,5,6,7,8,9中的一个数
2.将这个数字乘以9
3.将上面的结果乘以12 345 679
多选几个数试一试,你发现了什么规律?与同伴交流你的理由.
获取新知
一起探究
你从这些计算结果中发现了什么规律?
问题3 写出一个四位数,它的各个数位上的数字各不相等(如6731),用这个四位数各个数位上的数字组成一个最大数和一个最小数,并用最大数减去最小数,得到一个新的四位数,重复上面的过程,又得到一个新的四位数.一直重复下去,你发现了什么?请借助计算器帮助你进行探索.
“黑洞”数:6174
1. 利用计算器计算(说明按键方法及运算结果.
解:(1) 0;(2) 4;(3) 2 (4) -3.
2. 若按键顺序为: ,则与其对应的算式是______________.
(-)
3
x2
2
yx
4
=
+
随堂演练
1 ×1=_____;11 ×11=_______; 111 ×111=_________.
3.用计算器探索:
(1)用计算器计算:
(2)根据(1)的计算结果,总结规律,不用计算器,试直接写出下列式子的答案.
1111 ×1111=_________; 111111×111111=____________;
111111111×111111111=___________________.
1
121
12321
1234321
12345654321
12345678987654321
计算器的使用
利用计算器计算
利用计算器探索规律
课堂小结
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
